图像处理--图像的几何变换--旋转变换

原博客：http://blog.csdn.net/linshanxian/article/details/68944748

旋转有一个绕着什么转的问题。通常的做法是以图像的中心为圆心旋转，将图像上的所有像素都旋转一个相同的角度。图像的旋转变换是图像的位置变换，但旋转后图像的大小一般会改变。和平移变换一样，既可以把转出显示区域的图像截去，也可以扩大显示区域以显示完整的图像，如下图所示。

我们先讨论不裁剪转出部分，扩大显示区域的情况。在下图所示的平面坐标系中，A0逆时针旋转θ变成A1，r是该点到原点的距离，则旋转前：

旋转后A1的坐标为

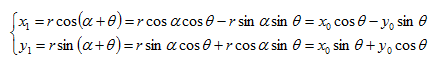
写成矩阵的形式为：

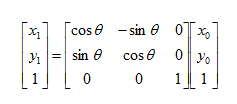
其逆变换矩阵如下：

上面公式是旋转变换的基本公式，坐标系是以图像的中心为原点，向右为x轴正方向，向上为y轴正方向。上述旋转是绕坐标原点进行的，如果是绕指定点（a,b）旋转，那么应该先将坐标系平移至改点，再旋转，然后平移至新的坐标原点。

下面推导坐标系平移的变换公式。坐标系Ⅰ是图像的坐标系，坐标系Ⅱ是旋转坐标系，坐标系Ⅱ的原点在坐标系中为（a,b），如下图所示。

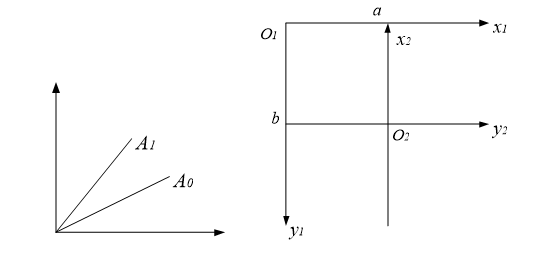
两种坐标系之间的转换为：

逆变换为：

有了上面的公式，就可以很方便的推导图像旋转变换的表达式。假设图像未旋转时候旋转中心的坐标是（a,b），旋转后中心点的坐标为（c,d）（在新的坐标系下，以旋转后图像的左上角为原点），则可以把变换分为3步：

第一步，将坐标系Ⅰ变成Ⅱ；

第二步，旋转θ（逆时针为正，顺时针为负）；

第三步，将坐标系Ⅱ变换回Ⅰ。这样就得到了总的变换矩阵。

设原图像某像素点的坐标为(x0，y0)，旋转后在目标图像的坐标为(x1，y1)，则旋转变换的矩阵表达式为：

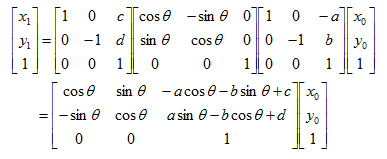
逆变换为：

有了上面的转换公式，就可以很方便的编写出实现图像旋转的程序。首先需要计算出公式中需要的几个参数：a、b、c、d和旋转后图像的尺寸。已知原是图像的宽度为w0，高度为h0，以图像的中心为坐标原点。则原图像四个角的坐标分别是：

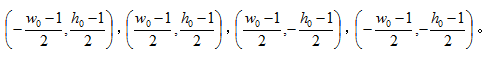
按照旋转公式，旋转后这四个点的坐标分别是：

则新图像的高度和宽度分别为：

令

图像旋转的主要代码如下：

void RotIamge(const Mat &srcImage, Mat &dstImage, double angle)  
{  
    //弧度  
    double sita = angle * CV_PI / 180;  
    double a = (srcImage.cols - 1) / 2.0;  
    double b = (srcImage.rows - 1) / 2.0;  
  
    int srcRow = srcImage.rows;  
    int srcCol = srcImage.cols;  
  
    double x1 = -a * cos(sita) - b * sin(sita);  
    double y1 = -a * sin(sita) + b * cos(sita);  
  
    double x2 = a * cos(sita) - b * sin(sita);  
    double y2 = a * sin(sita) + b * cos(sita);  
  
    double x3 = a * cos(sita) + b * sin(sita);  
    double y3 = a * sin(sita) - b * cos(sita);  
  
    double x4 = -a * cos(sita) + b * sin(sita);  
    double y4 = -a * sin(sita) - b * cos(sita);  
  
    int w1 = cvRound(max(abs(x1 - x3), abs(x4 - x2)));  
    int h1 = cvRound(max(abs(y1 - y3), abs(y4 - y2)));  
    dstImage.create(h1, w1, srcImage.type());  
  
    double c = (w1 - 1) / 2.0;  
    double d = (h1 - 1) / 2.0;  
  
    double f1 = -c * cos(sita) + d * sin(sita) + a;  
    double f2 = -c * sin(sita) - d * sin(sita) + b;  
    int nRowNum = dstImage.rows;  
    int nColNum = dstImage.cols;  
    for (int i = 0; i < nRowNum; i++)  
    {  
  
        for (int j = 0; j < nColNum; j++)  
        {  
            int x = cvRound(j * cos(sita) - i * sin(sita) + f1);  
            int y = cvRound(j * sin(sita) + i * cos(sita) + f2);  
            if (x > 0 && x < srcCol && y > 0 && y < srcRow)  
            {  
                dstImage.at(i, j) = srcImage.at(y, x);  
            }  
        }  
    }  
}  

对于旋转以后图像大小不变的情况，旋转前后图像的中心点坐标都是（a,b），那么旋转的变换矩阵就是：

逆变换为：

公式中，

主要代码如下：

void RotIamge2(const Mat &srcImage, Mat &dstImage, double angle)  
{  
    //弧度  
    double sita = angle * CV_PI / 180;  
    double a = (srcImage.cols - 1) / 2.0 + 0.5;  
    double b = (srcImage.rows - 1) / 2.0 + 0.5;  
  
    int nRowNum = srcImage.rows;  
    int nColNum = srcImage.cols;  
    dstImage.create(nRowNum, nColNum, srcImage.type());  
  
    double f1 = -a * cos(sita) + b * sin(sita) + a;  
    double f2 = -a * sin(sita) - b * cos(sita) + b;  
  
    for (int i = 0; i < nRowNum; i++)  
    {  
        for (int j = 0; j < nColNum; j++)  
        {  
            int x = cvRound(j * cos(sita) - i * sin(sita) + f1);  
            int y = cvRound(j * sin(sita) + i * cos(sita) + f2);  
            if (x > 0 && x < nColNum && y > 0 && y < nRowNum)  
            {  
                dstImage.at(i, j) = srcImage.at(y, x);  
            }  
        }  
    }  
}  

要注意的是，由于有浮点运算，计算出来的坐标可能不是整数，需要采取取整处理，使用cvRound()函数寻找最接近的点，这样会带来一些误差，图像可能会出现锯齿，更好的方式是采用插值，后续将会具体介绍。