流体力学
一、概述
流体力学是研究流体宏观平衡和运动规律的一门学科，是力学的一个分支。其研究的对象包括液体和气体，统称流体。
二、研究方法
分为三个方面：理论分析法、实验方法、数值分析方法。
三、流体连续介质假设
从分子角度看，流体之间总是存在间隙，其质量在空间的分布是不连续的，其运动在时间和空间上都是不连续的。为了准确描述大量分子的统计平均特性的空间分布，如密度、压力和温度的空间分布等，为此建立流体质点的概念。建立流体质点之后，可认为流体内的每一点都被占据，中间无空隙，因此流体的任意物理参数（密度、压力、速度等）都可表示为空间坐标和时间的连续函数，且都是连续可微函数。
该假设除稀薄气体和激波等少数情况外的大多数场合都是适用的。
四、流体的密度、比体积和相对密度
密度： 
比体积： 
相对密度： 
水的相对密度为1，水银的相对密度为13.6
五、流体的主要物理特性
1.压缩性
通常以体积压缩率来表示，表示温度不变的情况下，单位压强增量引起的流体体积的相对变化量。
体积压缩率： 
体积模量： 
2.膨胀性
通常用膨胀体膨胀系数来表示，表示压强不变的情况下，单位温度升高所引起的流体体积相对变化量。
3.粘性
（1）粘性是流体抵抗剪切变形的一种属性，是流体运动时内部流层之间产生切应力（内摩擦力）的性质。
因为各流层速度不同，流体层之间会出现相对运动，产生的切向作用力称为内摩擦力。作用在两流体层接触面上的内摩擦力总是成对出现且大小相等，方向相反，分别作用在相对的流层上。
（2）牛顿内摩擦定律：据牛顿平板实验的结果，作用在上平板的力的大小与垂直于流动方向的速度梯度成正比，与接触面的面积成正比，并与流体的物理属性（粘度）有关，而与接触面的压强无关。
流体层间单位面积上的内摩擦力称为粘性切应力：
（3）粘度：表征流体粘性大小的物理量。
压强和温度对流体的粘性都有影响。压强的加大将使分子间的距离减小，粘度增大；温度升高时，流体分子间的距离增加，液体粘度减小，气体分子的不规则运动加剧，动量交换更加频繁，气体的粘度将增大。
六、流体模型分类
1.无粘性流体和粘性流体
真实的流体具有粘性。若研究流体力学问题时不考虑粘度对流体流动的影响，则把这样的流体称为无粘性流体，需要考虑粘度对流体的影响的流体称为粘性流体。
2.可压缩流体和不可压缩流体
（1）液体可压缩性很小，完全可以忽略。其他液体与水相似，因此一般情况下液体作为均质不可压缩流体模型处理，即认为密度为常数。
（2）气体在没有热交换的情况下做低速流动时，密度变化的影响可以忽略不计。
（3）即无粘性又不可压缩的流体称为理想流体。
七、流体力学中的三大基本方程
1.连续性微分方程
理论依据：质量守恒定律在微元体中的应用。
数学描述：[单位时间流出的质量]-[单位时间流入的质量]+[单位时间质量的累积或者增量]=0
公式推导：
（1）单位时间内流入、流出微原体流体总质量变化
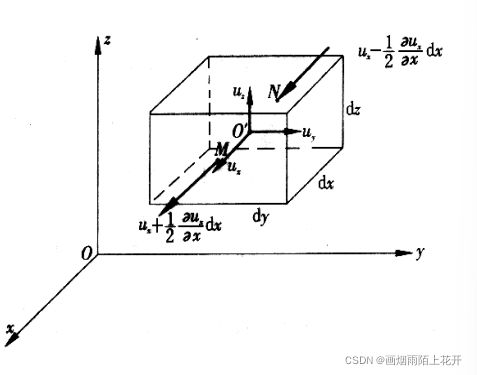
假定流体连续地充满整个流场，从中任取出以O'（x,y,z）点为中心的微小六面体空间作为控制体。控制体的边长为dx,dy,dz,分别平行于直角坐标轴x,y,z。设控制体的中心点处流速的三个分量为
，液体密度为
。将各流速分量按泰勒级数展开，并略去高阶微量，可得到该时刻通过控制体六个面表面中心点的流体质点的运动速度。例如：通过控制体前表面中心点M的质点在x方向的分速度为
通过控制体后表面中心点N的质点在x方向的分速度为
因所取控制体无限小，故认为在其各表面上的流速均匀分布。
所以单位时间内沿x轴方向
流入控制体的质量为 ![\left [ \rho v_{x}-\frac{1}{2}\frac{\partial \left ( \rho v_{x} \right )}{\partial x} dx\right ]dydz](http://img.e-com-net.com/image/info8/47fc82ff17fd4a588e5e76b95a40e006.png){kind=small}
流出控制体的质量为 ![\left [ \rho v_{x}+\frac{1}{2}\frac{\partial \left ( \rho v_{x} \right )}{\partial x} dx\right ]dydz](http://img.e-com-net.com/image/info8/0728a65424924884a72c9310584260e8.png){kind=small}
于是，单位时间内在x方向流出与流入控制体的质量之差为
同理可得在单位时间内沿y,z方向流出与流入控制体的质量之差为
故单位时间内流入流出微元体流体的质量总变化为
![\left [\frac{\partial\left ( \rho v_{x} \right ) }{\partial x} +\frac{\partial\left ( \rho v_{y} \right ) }{\partial y}+\frac{\partial\left ( \rho v_{z} \right ) }{\partial z} \right ]dxdydz](http://img.e-com-net.com/image/info8/9a853d79ea3d411a95819a2d5b39d3dd.png){kind=small}
（2）控制体内质量变化
由于控制体是固定的，质量变化是因密度变化引起的，dt时间内：
单位时间内，微元体质量增量为
（微团密度在单位时间内的变率与微团体积的乘积）
（3）根据连续性条件
矢量形式： (三维连续性微分方程)
（1）适用条件：不可压缩和可压缩流体、理想和实际流体、稳态和非稳态流动
（2）不可压缩性流体的连续性微分方程:
说明流体变形率为零，即流体不可压缩或者流入体积流量与流出体积流量相等。
（3）稳定流动时：所有流体物体性质参数均不随时间而改变。
2.理想流体的运动方程
理论依据：牛顿第二定律在流体力学上的具体应用，建立了理想流体的密度、速度、压力与外力之间的关系。
推导过程：
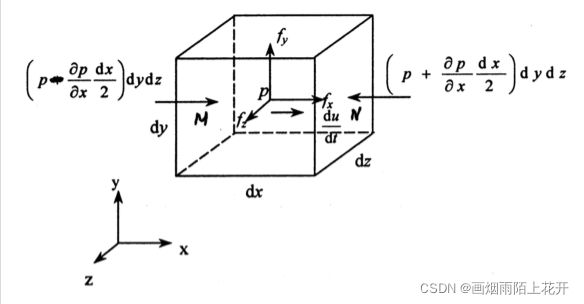
（1）取微小六面控制体
（2）推导依据：
牛顿第二定律或者动量定理：作用力之合力=动量随时间的变化速率
（3）分析受力：
a.质量力：是某种力场作用在全部流体质点上的力，其大小和流体的质量或体积成正比。
单位质量力：
x方向上所受到的质量力：
b.表面力：理想流体，没有粘性，所以表面力只有压力
概念：作用在所研究流体外表面上与表面积大小成正比的力，表面力与流体的表面积成正比。作用于流体中任一微小表面上的力又可分为两类，即垂直于表面的力和平行于表面的力。前者为压力，后者为剪力（切力）。静止流体只受到压力的作用，而流动流体则同时受到两类表面力的作用。表面力可以分为沿表面内法向的法向分力和沿着表面切向的摩擦力。
x方向上作用于垂直x轴方向两个面的压力分别为：
x方向上质点所受所受到表面力合力：
c.流体质点加速度
的计算方法即流速的全导数：
由于
所以流体质点的加速度即流速的全导数为
流体质点加速度在三个坐标轴上的分量分别为
（4）代入牛顿第二定律求得运动方程：
得x方向上的运动微分方程：
单位体积流体的运动微分方程：
单位质量流体的运动微分方程：
同理可以得到y,z方向上的：
向量形式：
(理想流体欧拉运动微分方程)
其中，
适用条件：理想流体，不可压缩流体和可压缩流体
未完待更新……