1 八皇后问题

算法

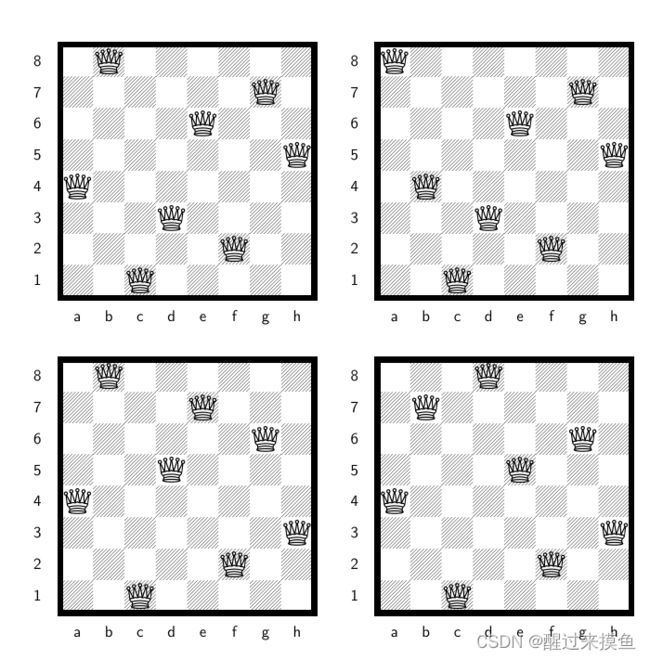
  八皇后问题是在国际象棋的棋盘上放八个皇后，八个皇后不能互相攻击。国际象棋的皇后，可以横向攻击也可以纵向攻击，也可以斜向攻击。所以要放八个皇后，就必须任一直线和斜线上不能同时有两个皇后。比如以下就是一个八皇后方案：

  解决八皇后问题的算法是回溯法，因为穷举法需要循环的次数太多，所以用回溯法。其基本思想如下：
  循环遍历行，在循环中：

1. 如果成功，跳到下一行；
2. 如果失败，回到上一行，寻找下一个位置
3. 如果到了第一行最后一个位置，那么就失败了。

代码

  代码如下：

public static final int SIZE = 8;

public static void main(String[] args) {
    // 用一个数组来显示
    final int[] ints = {-1, -1, -1, -1, -1, -1, -1, -1};
    int r = 0;
    for (;r >=0 && r < SIZE; ) {
        int column = findPosition(ints, r);
        // 找不到
        if (column < 0) {
            ints[r] = -1;
            r--;
        } else {
            ints[r] = column;
            r++;
        }
    }
    final Chessboard chessboard = new Chessboard(ints);
    System.out.println(chessboard);
}

/**
 * 找第row行的合法位置
 * @param ints
 * @param row
 * @return
 */
private static int findPosition(int[] ints, int row) {
    // begin at next column
    final int column = ints[row] + 1;
    for (int c = column; c < SIZE; c++) {
        if (valid(ints, row, c)) {
            return c;
        }
    }
    return -1;
}

private static boolean valid(int[] ints,int row, int c) {
    // 在第几行上
    // 循环啊
    for (int i = 0; i < row; i++) {
        // 如果同一列
        final int otherC = ints[i];
        if (otherC == c) {
            return false;
        }
        // 如果是斜对角,比如对方是 r0 c2 我是 r1 c3
        // 或者我是r1 c1 row - i 是行数差  other c - c 为列数差
        if (row - i == Math.abs(otherC - c)) {
            return false;
        }
    }
    return true;
}

  那么如何计算出所有的八皇后方案呢？上面的代码是不行的，只能找到一种方案，要找到所有的方案就必须修改算法了。

所有方案算法

  如果要遍历所有的方案，很明显可以看出这是个树形结构，前N行构成一种方案，但是在N+1行时可能就有不止一种方案了，这样就形成了分支，所以整个方案就构成了一个树形结构了。所以先简单做一个树形结构，再对这个树形结构进行回溯法搜索。
  我用穷举法实现了，总共92种解法。首先是树的代码：

package com.trend;

import java.util.ArrayList;
import java.util.Collections;

/**
 * 方案树
 *
 * @author a simple coder
 * @since 1.0.0
 * created in 2023/5/31, 星期三
 */
public class SolutionTree {

    private Node root;

    public SolutionTree(int i) {
        Node node = new Node();
        node.setRow(0);
        node.setColumn(i);
        root = node;

    }

    public Node getRoot() {
        return root;
    }

    public void setRoot(Node root) {
        this.root = root;
    }

    public static class Node {

        private int column;
        private int row;
        private Node[] children;

        private Node parent;

        public int getColumn() {
            return column;
        }

        public void setColumn(int column) {
            this.column = column;
        }

        public int getRow() {
            return row;
        }

        public void setRow(int row) {
            this.row = row;
        }

        public Node[] getChildren() {
            return children;
        }

        public void setChildren(Node[] children) {
            this.children = children;
            for (Node node:children) {
                node.parent = this;
            }
        }

        public Node getParent() {
            return parent;
        }

        public void setParent(Node parent) {
            this.parent = parent;
        }

        public void remove(Node pop) {
            ArrayList<Node> nodes = new ArrayList<>();
            for (Node node: children) {
                if (node != pop) {
                    nodes.add(node);
                } else {
                    node.parent = null;
                }
            }
            this.children = nodes.toArray(new Node[0]);
        }

        @Override
        public String toString() {
            return "Node{" +
                    "column=" + column +
                    ", row=" + row +
                    '}';
        }

        public String path() {
            StringBuilder stringBuilder = new StringBuilder();
            for (SolutionTree.Node start = this; start != null; start = start.getParent()) {
                stringBuilder.append(start.column).append(">-");
            }
            return stringBuilder.reverse().toString();
        }

        public String latex(int size) {

            ArrayList<String> strings = new ArrayList<>();
            int i=size;
            for (SolutionTree.Node start = this; start != null; start = start.getParent()) {
                strings.add("Q"+(char)('a'+start.column)+(i--)+"");
            }
            Collections.reverse(strings);
            String x = String.join(",", strings);
            return  "\\chessboard[\n" +
                    "\tstyle=8x8,\n" +
                    "\tsetpieces={"+x+"},\n" +
                    "\tpadding=1ex,\n" +
                    "\t]";
        }
    }
}

  然后是逻辑代码：

package com.trend;

import java.util.*;

/**
 * 八皇后
 *
 * @author a simple coder
 * @since 1.0.0
 * created in 2023/5/31, 星期三
 */
public class EightQueens {

    public static final int SIZE = 8;

    public static void main(String[] args) {
        // 用一个数组来显示
        // 初始化8种方案
        int size = 0;
        for (int i = 0; i < SIZE; i++) {
            SolutionTree solutionTree = getSolutionTree(i);

            ArrayDeque<SolutionTree.Node> nodes = new ArrayDeque<>();
            nodes.add(solutionTree.getRoot());
            while (!nodes.isEmpty()) {
                SolutionTree.Node pop = nodes.pop();
                SolutionTree.Node[] children = pop.getChildren();
                if (children != null) for (SolutionTree.Node n : children) {
                    nodes.add(n);
                }
                if (pop.getRow() == SIZE - 1) {
                    System.out.println(pop.latex(SIZE));
                    size++;
                }
            }
        }
        System.out.println(size);

    }

    private static SolutionTree getSolutionTree(int start) {
        SolutionTree solutionTree = new SolutionTree(start);
        SolutionTree.Node root = solutionTree.getRoot();
        ArrayDeque<SolutionTree.Node> nodes = new ArrayDeque<>();
        nodes.add(root);
        while (!nodes.isEmpty()) {
            SolutionTree.Node pop = nodes.pop();
            List<Integer> positions = findPositions(pop);
            if (pop.getRow() == SIZE - 1) {
                continue;
            }
            if (positions.isEmpty()) {
                // 删除当前节点
                if (pop.getParent() != null) pop.getParent().remove(pop);
            } else {
                SolutionTree.Node[] children = new SolutionTree.Node[positions.size()];
                int i = 0;
                for (int position : positions) {
                    SolutionTree.Node node = new SolutionTree.Node();
                    node.setRow(pop.getRow() + 1);
                    node.setColumn(position);
                    children[i++] = node;
                    nodes.push(node);
                }
                pop.setChildren(children);
            }
        }
        return solutionTree;
    }


    /**
     * 找第row行的合法位置
     *
     * @param node 解决方案树的节点
     * @return
     */
    private static List<Integer> findPositions(SolutionTree.Node node) {
        // 本节点的所在行
        ArrayList<Integer> integers = new ArrayList<>();
        // begin at next column
        final int column = 0;
        for (int c = column; c < SIZE; c++) {
            if (valid(node, c)) {
                integers.add(c);
            }
        }
        return integers;
    }

    /**
     * 验证是否有效
     *
     * @param node   结点
     * @param row    第几行
     * @param column 第几列
     * @return 是否有效
     */
    private static boolean valid(SolutionTree.Node node, int column) {
        // 在第几行上
        // 循环啊
        int row = node.getRow() + 1;
        for (SolutionTree.Node start = node; start != null; start = start.getParent()) {

            // 如果同一列
            final int otherC = start.getColumn();
            if (otherC == column) {
                return false;
            }

            // 如果是斜对角,比如对方是 r0 c2 我是 r1 c3
            // 或者我是r1 c1 row - i 是行数差  other c - c 为列数差
            if (row - start.getRow() == Math.abs(otherC - column)) {
                return false;
            }
        }
        return true;
    }


}

  最终结果里我取了四个，大概就是这样子：