中文信息处理(六)—— 神经语言模型与词表示(word2vec)
文章目录
-
- 1. 基于神经网络语言模型
-
- 1.1 几种语言模型对比
- 1.2 神经网络语言模型 NNLM
-
- 第一层(输入层)
- 第二层(隐藏层)
- 第三层(输出层)
- 1.3 小结
- 2. word2vec
-
- 2.2.1 CBOW
-
- 基于层次softmax的CBOW
- 参数估计
- 参数优化
- 2.2.2 Skip-gram
-
- 负采样
- 2.2.3 gensim中的word2vec
- 2.2.4 Word2vec 参数选择(经验性结论)
1. 基于神经网络语言模型
The Neural History of NLP
| Time | The Neural History of NLP |
|---|---|
| 2001 | Neural language models |
| 2008 | Multi-task learning |
| 2013 | Word embeddings |
| 2013 | Neural networks for NLP |
| 2014 | Sequence-to-sequence models |
| 2015 | Attention |
| 2015 | Memory-based networks |
| 2018 | Pretrained language models |
这些模型后面的文章大部分都会提到
神经网络词向量表示技术通过神经网络技术对上下文,以及上下文与目标词之间的关系进行建模。由于神经网络较为灵活,这类方法的最大优势在于可以表示复杂的上下文
1.1 几种语言模型对比
语言模型
P ( s ) = P ( w 1 ) × P ( w 2 ∣ w 1 ) × ⋯ × P ( w 1 ∣ w 1 ∣ . w 1 − w m ∣ = ∏ 1 = 1 m ∣ P ( w 1 ∣ w 1 ∣ − 1 ) \left. \begin{array} { l } { P ( s ) = P ( w _ { 1 } ) \times P ( w _ { 2 } | w _ { 1 } ) \times \cdots \times P ( w _ { 1 } | w _ { 1 } | . w _ { 1 } - w _ { m } | } \\ { = \prod _ { 1 = 1 } ^ { m } | P ( w _ { 1 } | w _ { 1 } | _ { - 1 } ) } \end{array} \right. P(s)=P(w1)×P(w2∣w1)×⋯×P(w1∣w1∣.w1−wm∣=∏1=1m∣P(w1∣w1∣−1)
N-gram 语言模型
P ( s ) = ∏ t P ( w t ∣ w t − n + 1 ⋯ , w t − 1 ) P ( s ) = \prod _ { t } P ( w _ { t } | w _ { t - n + 1 } \cdots , w _ { t - 1 } ) P(s)=t∏P(wt∣wt−n+1⋯,wt−1)
神经网络语言模型 NNLM
P ( s ) = ∏ t P ( w t ∣ w t − n + 1 ⋯ , w t − 1 ) P ( s ) = \prod _ { t } P ( w _ { t } | w _ { t - n + 1 } \cdots , w _ { t - 1 } ) P(s)=t∏P(wt∣wt−n+1⋯,wt−1)
1.2 神经网络语言模型 NNLM
对于整个模型而言,输入为条件部分的整个词序列: w i − ( n − 1 ) ; : : : ; w i − 1 , w i w_{i-(n-1)}; : : : ;w_{i-1},w_i wi−(n−1);:::;wi−1,wi
输出为目标词的分布(词向量)
第一层(输入层)
将词在高维空间映射为单词的词向量
这个模型首先将词典中的单词映射到一个给定维度k的高维空间,这个映射就是图中的参数矩阵C(该矩阵行数等于词典中的单词数量,列数等于给定的高维空间的维度k)。单词在高维空间的映射就是单词的词向量表达 。
将 C ( w t − n − 1 ) … C ( w t − 2 , C ( w t − 1 ) C(w_{t-n-1})…C(w_{t-2},C(w_{t-1}) C(wt−n−1)…C(wt−2,C(wt−1)这n-1个向量受委相接,形成一个 ( n − 1 ) k (n-1)k (n−1)k维的向量 X X X
第二层(隐藏层)
与一般神经网络相同,直接使用线性函数 X W + b XW+b XW+b计算得到。
在此之后,使用 tanh 作为激活函数。将每个单词对应的上下文映射到词典全部单词对应
的条件概率分布空间中。
h 1 = tanh ( X W h 1 + b 1 ) (1) h_1=\tanh ( X W _ { h 1 } + b _ { 1 } ) \tag{1} h1=tanh(XWh1+b1)(1)
第三层(输出层)
每个节点yi表示下一个词为i的未归一化 log概率。使用softmax激活函数将输出值y归一化成概率。
y = tanh ( X W h 1 + b 1 ) U + X W r + b r (2) y = \tanh ( X W _ { h 1 } + b _ { 1 } ) U + X W _ { r } + b _ { r } \tag{2} y=tanh(XWh1+b1)U+XWr+br(2)
注意到,此式相当于进行了一次拼接,将输入的 X X X直接加到输出(图中的虚线),所以直连边就是从输入层直接到输出层的一个线性变换。
不经过中间的隐藏层,为的是防止隐藏层将一些重要的特征去掉。但是大量的实验表明,如果没有直连边,可以语言模型反而性能更好;有直连边,则加快了速度(减少一半的迭代次数)。因此在后续工作中,很少有使用输入层到输出层直连边的工作。
1.3 小结
对于整个语料而言,语言模型需要最大化:
∑ w i − ( n − 1 ) : E D log P ( w i − ( n − 1 ) x − 1 ) ⋯ w i − 1 (3) \sum _ { w _ { i } - ( n - 1 ) : E D } \log P ( w _ { i - ( n - 1 ) } x - 1 ) \cdots w _ { i - 1 } \tag{3} wi−(n−1):ED∑logP(wi−(n−1)x−1)⋯wi−1(3)
使用梯度上升法对θ进行优化 。优化结束之后,就得到语言模型(1)式。
此时的参数C即为该最优模型下的词向量表示
2. word2vec
word2vec 在2013年被提出,论文原文被引用次数超过了10000次。
- CBOW:用上下文预测中间的词
- Skip-gram::用中间的词预测上下文
2.2.1 CBOW
- 输入层:上下文单词的onehot
- 所有onehot分别乘以共享的lookup矩阵E {V*N矩阵,N为设定词向量维度,随机初始化}
- 所得的向量相加求平均作为隐层向量(没有隐藏层)
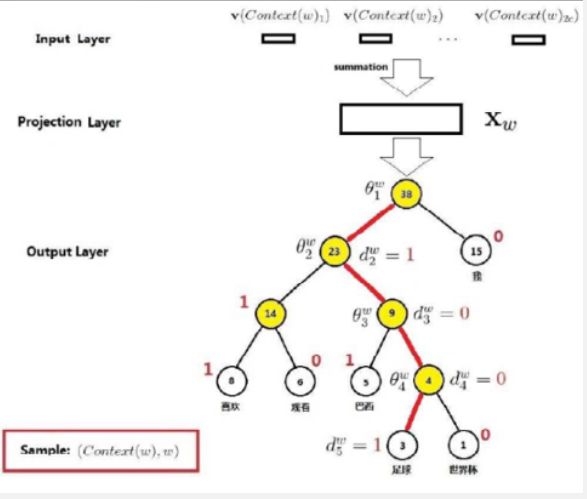
基于层次softmax的CBOW
使用Huffman编码减少编码长度,一百万个词,只需要22层树,运算量大幅度下降
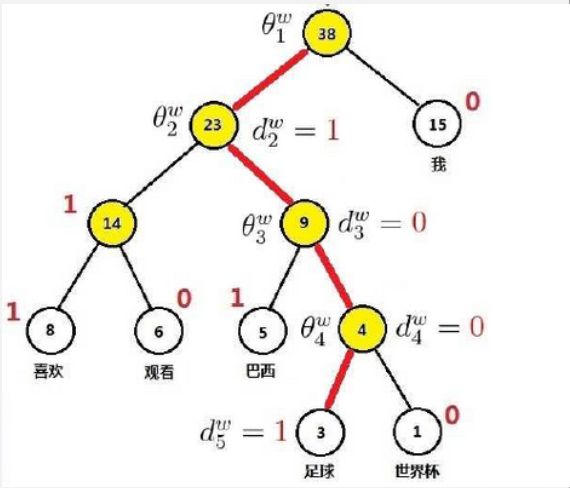
分别用字符 d 1 , d 2 … d n d_1,d_2…d_n d1,d2…dn作为叶子结点(叶节点个数为 N N N),各字符的使用频率 w 1 , w 2 , … , w n w_1, w_2, …, w_n w1,w2,…,wn作为叶子结点上的权,构造赫夫曼树。约定,W2V中规定权值大的设为左子节点标记为1,右子节点标记为0 (与Huffman树的常见标记反着),则从根到每个叶子结点路径上的二进制数字组成的序列就是该叶子结点中字符的编码。
输出层:对应一棵Huffuman树,它以词典中的词为叶节点,以词出现的次数为叶节点的权重来构建;每个非叶节点对应一个二分类器。
每个二分类器是一个逻辑回归分类器,概率表示为:
P ( d j w ∣ θ j − 1 w x w ) = [ Q ( θ j − 1 w T i v T ⋅ x i v j ) ] 1 − d w × [ 1 − G ( θ j − T w T w ) d (4) P ( d _ { j } ^ { w } | \theta _ { j - 1 } ^ { w } x _ { w } ) = [ Q ( \theta _ { j - 1 } ^ { w } T _ { i v } ^ { T } \cdot x _ { i v j } ) ] ^ { 1 - d ^ { w } } \times [ 1 - G ( \theta _ { j - T } ^ { w } T _ { w } ) ^ { d} \tag{4} P(djw∣θj−1wxw)=[Q(θj−1wTivT⋅xivj)]1−dw×[1−G(θj−TwTw)d(4)
那么,对于目标单词w的条件概率为:
P ( w ∣ context ( w ) ) = ∏ j = 2 k P ( d j w ∣ j − 1 w x w ) (5) P ( w | \operatorname { context } ( w ) ) = \prod _ { j = 2 } ^ { k } P ( d _ { j } ^ { w } | _ { j - 1 } ^ { w } x _ { w } ) \tag{5} P(w∣context(w))=j=2∏kP(djw∣j−1wxw)(5)
分类时,分到左边负类时,乘号左边起作用
参数估计
参数估计采用极大似然的思想,即找到一组参数,使得根据上下文context(w)预测为目标词w的“整体概率”最大
参数优化
W2V采用随机梯度上升法,对每个样本(context(w),w),就对所有的参数进行更新。独立地优化路径上每个二分类器的L(w, j),让每个L(w, j)同时往梯度上升的方向更新,逐步逼近整体最优 。
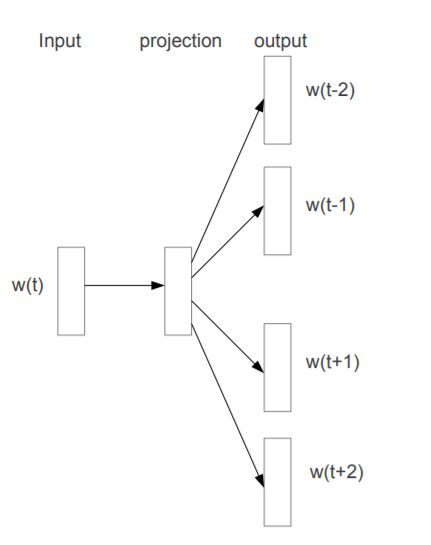
2.2.2 Skip-gram
Skip-Gram模型与CBOW相反。输入是特定的一个词的词向量,而输出是特定词对应的上下文词向量(即概率排前N的词)。
∑ w ∈ c log p ( C o n t e x t ( w ) ∣ w ) (6) \sum _ { w∈c } \log p (Contex t ( w ) | w ) \tag{6} w∈c∑logp(Context(w)∣w)(6)
∑ w ∈ V ∑ w c ∈ c o n t e x t ( w ) log P ( w c ∣ w ) (7) \sum _ { w∈V } \sum _ { w_c∈context( w ) } \log P ( w_c|w ) \tag{7} w∈V∑wc∈context(w)∑logP(wc∣w)(7)
p ( w O ∣ w I ) = exp ( v w O ′ ⊤ v w I ) ∑ w = 1 W exp ( v w ′ ⊤ v w I ) (8) p\left(w_{O} \mid w_{I}\right)=\frac{\exp \left(v_{w_{O}}^{\prime}{ }^{\top} v_{w_{I}}\right)}{\sum_{w=1}^{W} \exp \left(v_{w}^{\prime}{ }^{\top} v_{w_{I}}\right)} \tag{8} p(wO∣wI)=∑w=1Wexp(vw′⊤vwI)exp(vwO′⊤vwI)(8)
负采样
Skip-gram模型通常采用了基于负采样的方法进行优化 。
注意,在Word2Vec 实际实现中,并不是对上下文中的每一个词都进行了n 次负采样,而是仅进行了|context(w)| 次负采样操作
2.2.3 gensim中的word2vec
import gensim as gm
from gensim.models import word2vec
sens = word2vec.LineSentence("file.txt")
# one line = one sentence. Words must be already preprocessed and separated by
whitespace.
# sens:句子,min_count:词频小于设定值的词扔掉,window:一次取的词数,size:词向量的维度,sg:使用CBOW/Skip,hs:若为1采用树优化,worker:CPU并行数量,iter:最大迭代次数
model = gm.models.Word2Vec(sens, min_count=0, window=5,
size=128, sg=0, hs=0, negative=5, workers=8, iter=200)
# sg ({0, 1}, optional) 1 for skip-gram; 0 for CBOW.
# hs ({0, 1}, optional) If 1, hierarchical softmax will be used for model training. If
# 0, and negative is non-zero, negative sampling will be used.
# 也可以保存为txt
model.wv.save_word2vec_format("WV.model_128.bin",binary=True)
# 使用和输出
model =gm.models.KeyedVectors.load_word2vec_format("WV.model.bin", binary=True)
vector = model.word_vec['computer']
for w in model.vocab:
print(model.word_vec(w))
2.2.4 Word2vec 参数选择(经验性结论)
根据Lai S, Liu K, He S, et al. How to generate a good word embedding[J]. IEEE Intelligent Systems, 2016, 31(6): 5-14.
- 根据具体任务,选一个领域相似的语料,在这个条件下,语料越大越好
- 语料小(小于一亿词,约 500MB 的文本文件)的时候用 Skipgram 模型,语料大的时候用 CBOW 模型
- 设置迭代次数为三五十次,维度至少选50