Computer Graphics From Scratch - Chapter 1
下面是该章前面的链接:
Computer Graphics From Scratch-《从零开始的计算机图形学》简介
Chapter 1
- Introductory Concepts-介绍性概念
- 一、画布
-
- 1.1. 坐标系
- 二、颜色模型
-
- 2.1. [减色]色彩模型
- 2.2. 加色模型
- 2.3. 忘记细节
- 三、颜色深度和表示
- 四、颜色处理
- 五、场景
- 六、概括
Introductory Concepts-介绍性概念
光线追踪器和光栅器采用非常不同的方法将 3D 场景渲染到 2D 屏幕上。但是,这两种方法都有一些共同的基本概念。
在本章中,我们将探索画布,我们将在其上渲染图像的抽象表面; 我们将用来引用画布上像素的坐标系; 如何表示和操纵颜色; 以及如何描述 3D 场景以便我们的渲染器可以使用它。
一、画布
在本书中,我们将在画布上绘制东西:一个可以单独着色的矩形像素阵列。 这幅画布是显示在屏幕上还是印在纸上与我们的目的无关。我们的目标是在 2D 画布上表示 3D 场景,因此我们将专注于渲染到这个抽象的矩形像素阵列。
我们将使用一个非常简单的函数来构建本书中的所有内容,它将颜色分配给画布上的像素:
canvas.PutPixel(x, y, color)
此方法具有三个参数:x 坐标、y 坐标和颜色。 现在让我们关注坐标。
1.1. 坐标系
画布有一个宽度和一个高度,以像素为单位,我们称之为 Cw 和 Ch。 我们需要一个坐标系来引用它的像素。 对于大多数电脑屏幕来说,原点在左上角; x 向屏幕右侧增加,y 向底部增加,如图 1-1 所示。

图 1-1:大多数计算机屏幕使用的坐标系
由于视频内存的组织方式,这个坐标系对于计算机来说非常自然,但对于人类来说,它并不是最自然的。 相反,3D 图形程序员倾向于使用通常用于在纸上绘制图形的坐标系:原点在中心,x 向右增加,向左减少,而 y 向顶部增加,向下减少,如 在图 1-2 中。
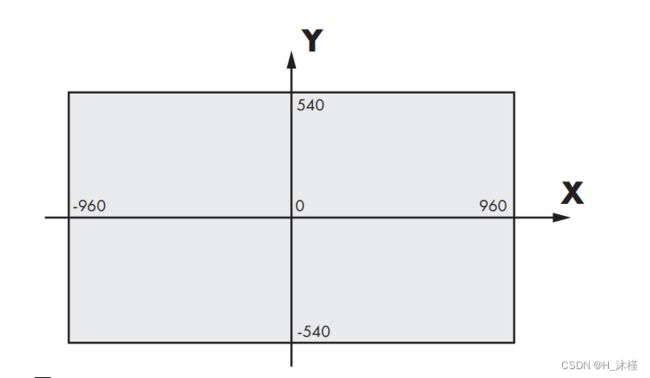
图 1-2:我们将用于画布的坐标系
使用这个坐标系,x坐标的范围是 [ − C w / 2 , C w / 2 ) [-Cw/2,Cw/2) [−Cw/2,Cw/2)
y坐标的范围是 [ − C h / 2 , C h / 2 ) [- Ch/2,Ch /2) [−Ch/2,Ch/2)
让我们假设对这些范围之外的坐标使用 PutPixel 函数什么都不做。
在我们的示例中,画布将绘制在屏幕上,因此我们需要从一个坐标系转换到另一个坐标系。 为此,我们需要改变坐标系的中心并反转 Y 轴的方向 【图1-1中的坐标系转换为图1-2】。 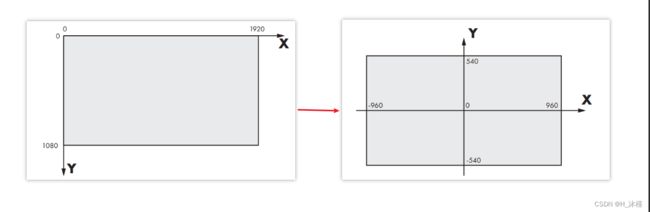
得到的转换方程是:
S x = C w / 2 + C x , S y = C h / 2 − C y Sx = Cw/2 + Cx, Sy = Ch/2 - Cy Sx=Cw/2+Cx,Sy=Ch/2−Cy
我们将假设 PutPixel 自动进行此转换;
从这一点开始,我们可以认为画布的坐标原点位于中心,x 向右增加,y 向屏幕顶部增加。
让我们看一下 PutPixel 的剩余参数:颜色。
二、颜色模型
颜色如何运作的理论很吸引人,但它超出了本书的范围。 以下是与我们相关的方面的简化版本。
当光线照射到我们的眼睛时,它会刺激眼睛后面的感光细胞。 这些会产生大脑信号它取决于入射光波的长度。 我们将这些大脑信号的主观体验称为颜色。
我们通常看不到可见范围之外的波长。 波长和频率成反比(波击中的频率越高,波峰之间的距离越小)。 这就是为什么红外线(波长超过 740 纳米,对应于低于 405 太赫兹 [THz] 的频率)是无害的,但紫外线(波长小于 380 纳米,对应于高于 790 太赫兹的频率)会灼伤您的皮肤。
可以想象的每种颜色都可以描述为这些颜色的不同组合。 “白色”是所有颜色的总和,而“黑色”是没有任何颜色。 通过描述颜色的确切波长来描述颜色是不切实际的; 幸运的是,几乎所有颜色都可以创建为三种颜色的线性组合,我们称之为原色。
2.1. [减色]色彩模型
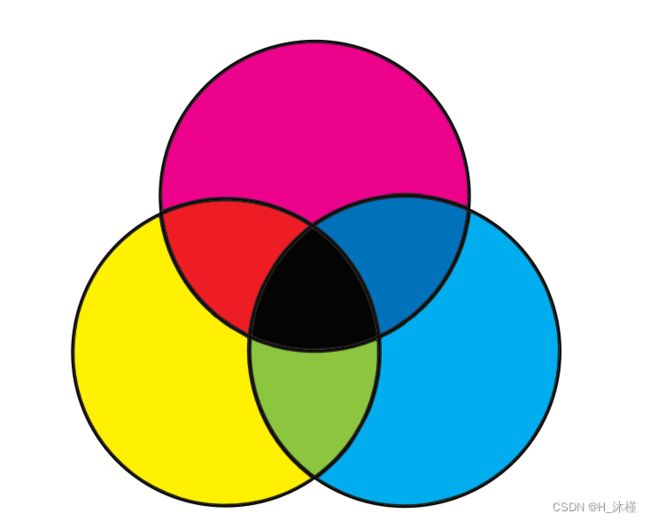
减色模型是您在蹒跚学步时用蜡笔所做的那件事的一个花哨的名字。 你拿一张白纸和红色、蓝色和黄色的蜡笔。 你画了一个黄色的圆圈,然后一个蓝色的圆圈覆盖它,你会得到绿色! 黄色和红色——橙色! 红色和蓝色——紫色! 将这三者混合在一起——有点黑暗! 幼儿园是不是很神奇? 图 1-3 显示了减色模型的原色,以及混合它们产生的颜色。
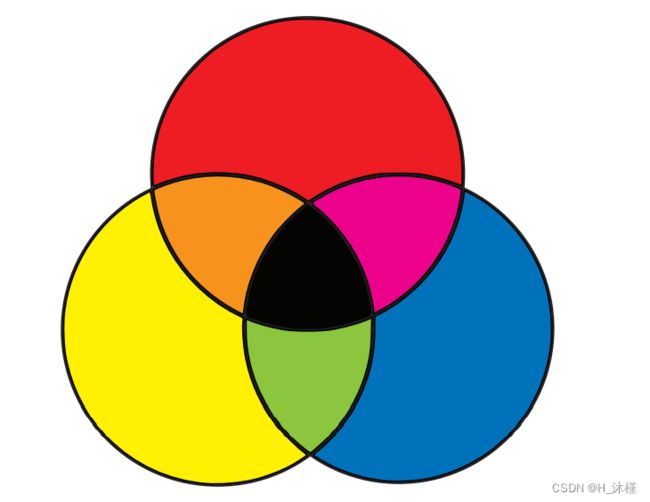
图 1-3:减色原色及其组合
在RYB(或减色)色彩模板中,红、黄、蓝是原色。
物体具有不同的颜色,因为它们以不同的方式吸收和反射光。 让我们从白光开始,比如阳光(阳光不是很白,但对于我们的目的来说已经足够接近了)。 白光包含各种波长的光。 当它撞击物体时,物体的表面会吸收一些波长并反射其他波长,具体取决于材料。 一些反射光然后照射到我们的眼睛上,我们的大脑将其转换为颜色。 什么颜色? 被表面反射的波长的总和。
那么蜡笔到底是怎么回事? 你从纸上反射的白光开始。 由于它是一张白纸,它反射了它接收到的大部分光线。 当你用“黄色”蜡笔画画时,你添加了一层材料,它吸收一些波长但让其他波长通过它。 它们被纸反射,再次穿过黄色层,撞到你的眼睛,你的大脑将这种特定的波长组合解释为“黄色”。 黄色层的作用是从原始白光中减去一堆波长。
您可以将每个彩色圆圈视为一个过滤器:当您绘制一个与黄色圆圈重叠的蓝色圆圈时,您会从原始光中过滤掉更多波长,因此映入您眼帘的是任何未被过滤的波长 蓝色或黄色圆圈,您的大脑将其视为“绿色”。
总之,我们从所有波长开始,减去一些原色以创建任何其他颜色。 这种颜色模型得名于我们通过减去波长来创建颜色的事实。
不过,这个模型并不完全正确。 减色模型中的实际原色不是教给幼儿和艺术学生的蓝色、红色和黄色,而是青色、洋红色和黄色。 此外,混合三种原色会产生一种不太黑的有点暗的颜色,因此添加纯黑色作为第四种“原色”。 因为 B 用于表示蓝色,黑色用 K 表示,因此我们得到 CMYK 颜色模型(图 1-4)。
您可以直接在彩色打印机的墨盒上看到这种颜色模型的证据,或者有时以廉价印刷的传单的形式出现,其中不同的颜色相互之间略有偏移。
图 1-4:打印机使用的四种减色原色
2.2. 加色模型
减色模型只是故事的一半。 如果您曾经近距离或用放大镜观看过屏幕(或者,说实话,不小心在屏幕上打了个喷嚏),您可能已经看到过彩色的小点:它们是红色、绿色和蓝色。
电脑屏幕与纸相反。 纸不发光; 它只是反射了部分照射到它的光。 另一方面,屏幕是黑色的,但它们确实会自行发光。 对于纸张,我们从白光开始,减去我们不想要的波长; 有了屏幕,我们从没有光开始,然后添加我们想要的波长。
我的理解是:不透明物体的颜色是由它们所反射的光所决定的。 在自然光中含有波长不同的各种色光,不同的物体吸收和反射不同种类的色光。 如果一个物体只能反射红光,而将红光以外的色光全部吸收,那么它就呈现红色。 如果它能反射所有颜色的光则呈现白色,如果它将几乎所有颜色的光都吸收了则呈现黑色。
为此需要不同的原色。
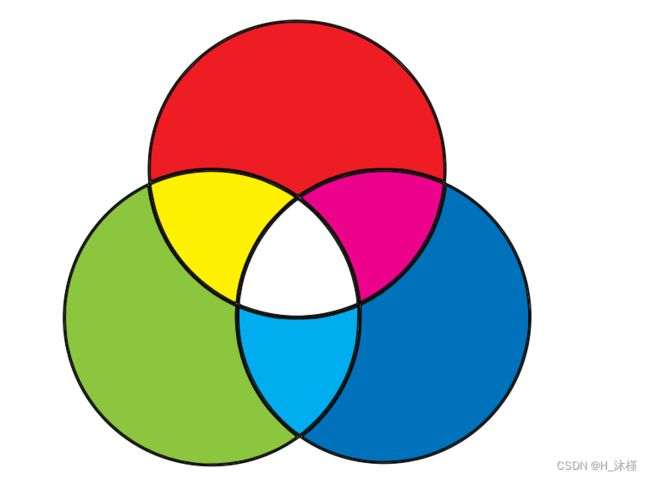
大多数颜色可以通过在黑色表面上添加不同数量的红色、绿色和蓝色来创建。 这是 RGB 颜色模型,一种加色模型,如图 1-5 所示。
加色原色的组合比其成分浅,而减色原色的组合更暗; 所有加法原色加起来为白色,而所有减色原色加起来为黑色。
图 1-5:加法原色及其组合
2.3. 忘记细节
既然你知道了这一切,你就可以选择性地忘记大部分细节,专注于对我们的工作重要的事情.
大多数颜色可以用 RGB 或 CMYK(或任何许多其他颜色模型),并且可以从一种颜色空间转换为另一种颜色空间。 因为我们专注于在屏幕上渲染事物,所以我们在本书的其余部分使用 RGB 颜色模型。
如上所述,物体吸收到达它们的部分光并反射其余部分。 哪些波长被吸收,哪些被反射,这就是我们所感知的表面的“颜色”。 从现在开始,我们将简单地将颜色视为表面的属性,而忽略光波长。
三、颜色深度和表示
显示器通过混合不同数量的红色、绿色和蓝色来创建颜色。 他们通过向它们提供不同的电压来以不同的强度照亮它们表面上的微小彩色点来做到这一点。
我们可以得到多少种不同的强度? 尽管电压是连续的,但我们将使用使用离散值(即数量有限)的计算机来处理颜色。 我们可以表示的红色、绿色和蓝色的色调越多,我们能够产生的颜色就越多。
你现在看到的大多数图像都使用每种原色 8 位,在这种情况下我们称之为颜色通道。 使用每个通道 8 位给我们每个像素 24 位,总共 224 种不同的颜色(大约 1670 万)。附:1 byte = 8 bit
这绝不是唯一可能的格式。 不久前,为了节省内存,流行15位和16位格式,在15位的情况下每个通道分配5位,红色5位,绿色6位,蓝色5位。 位大小写(称为 R5G6B5 或 565 格式)。 绿色得到了额外的一点,因为我们的眼睛对绿色的变化比对红色或蓝色的变化更敏感。
使用 16 位,我们得到 2^16 种颜色(大约 65,000 种)。 这意味着您在 24 位模式下每 256 种颜色获得一种颜色。 虽然 65,000 种颜色已经足够了,但对于颜色变化非常缓慢的图像,您将能够看到非常微妙的“阶梯”,这些“阶梯”在 1670 万种颜色中是不可见的,其中有足够的位来表示中间的颜色。 对于一些特殊的应用程序,例如电影的颜色分级,最好在每个通道使用更多的比特来表示更多的颜色细节。
我们将使用 3 个字节来表示一种颜色,每个字节保存一个 8 位颜色通道的值,从 0 到 255。我们将颜色表示为 (R, G, B),例如 (255, 0 , 0) 代表纯红色; (255, 255, 255) 代表白色; (255, 0, 128) 表示红紫色。
四、颜色处理
我们将使用一些操作来操纵颜色。 如果您了解一些线性代数,您可以将颜色视为 3D 颜色空间中的向量。 如果没有,请不要担心,我们将介绍我们现在将使用的基本操作。
我们可以通过将每个颜色通道乘以一个常数来修改颜色的强度:
k ( R , G , B ) = ( k R , k G , k B ) k(R, G, B) = (kR, kG, kB) k(R,G,B)=(kR,kG,kB)
例如,(32, 0, 128) 的亮度是 (16, 0, 64) 的两倍。
我们可以通过分别添加它们的颜色通道来将两种颜色添加在一起:
( R 1 , G 1 , B 1 ) + ( R 2 , G 2 , B 2 ) = ( R 1 + R 2 , G 1 + G 2 , B 1 + B 2 ) (R1, G1, B1) + (R2, G2, B2) = (R1 + R2, G1 + G2, B1 + B2) (R1,G1,B1)+(R2,G2,B2)=(R1+R2,G1+G2,B1+B2)
例如,如果我们想组合红色 (255, 0, 0) 和绿色 (0, 255, 0),我们将它们逐个通道相加并得到 (255, 255, 0),即黄色。
这些操作可能会产生无效值; 例如,将 (192, 64, 32) 的强度加倍会产生超出我们颜色范围的 R 值。 我们将任何大于 255 的值视为 255,将任何小于 0 的值视为 0; 我们称这个为 [0-255] 范围内的值。 这或多或少等同于您在现实生活中拍摄曝光不足或过度曝光的照片时发生的情况:您会得到全黑或全白的区域。
这就是我们关于颜色和 PutPixel 的入门知识的总结。 在我们进入下一章之前,让我们花一点时间探索如何表示我们将要渲染的 3D 对象。
五、场景
到目前为止,我们已经介绍了画布,我们可以在其上为像素着色的抽象表面。 现在我们通过引入另一个抽象来将注意力转向我们感兴趣的对象:场景。
场景是您可能对渲染感兴趣的一组对象。 它可以代表任何东西,从漂浮在空旷的无限空间中的单个球体(我们将从那里开始)到脾气暴躁的食人魔鼻子内部的极其详细的模型。
我们需要一个坐标系来讨论场景中的对象。 我们不能使用与画布相同的坐标系,原因有两个。 首先,画布是 2D,而场景是 3D。 其次,画布和场景使用不同的单位:画布使用像素,场景使用现实世界的单位(例如英制或公制)。
轴的选择是任意的,所以我们会选择一些对我们的目的有用的东西。 我们会说 Y 是向上的,X 和 Z 是水平的,并且所有三个轴都相互垂直。 将平面 XZ 视为“地板”,而 XY 和 YZ 是方形房间中的垂直“墙”。 这与我们为画布选择的坐标系一致,其中 Y 向上,X 水平。 图 1-6 显示了它的外观。
图 1-6:我们将用于场景的坐标系
场景单元的选择有些随意; 这取决于你的场景代表什么。 如果您正在模拟一个茶杯,“1”的测量值可能意味着 1 英寸,或者如果您正在模拟太阳系,它可能意味着 1 个天文单位。 只要我们始终如一地使用我们选择的单位,它们是什么都没有关系,所以我们从现在开始可以放心地忽略它们。
六、概括
在本章中,我们介绍了画布,一种表示我们可以在其上绘制的矩形表面的抽象,以及我们将在其上构建其他所有东西的一个方法:PutPixel。 我们还选择了一个坐标系来引用画布上的像素,并描述了一种表示这些像素颜色的方法。 最后,我们介绍了场景的概念,并选择了在场景中使用的坐标系。
奠定了这些基础之后,就该开始在它们之上构建光线追踪器和光栅化器了。