【MVS+DepthFilter】video-based real-time multi view stereo

1.SVO 半直接视觉里程计
2. SVO2系列之深度滤波DepthFilter
3. SVO（SVO: fast semi-direct monocular visual odometry）
4. svo_note
5. MVS+DepthFilter: video-based real-time multi view stereo
6. 作者George Vogiatzis主页

0. Abstract

本文介绍一种新颖的基于视频流的多视角立体重建算法，适用于手持相机进行实时交互式 3D 建模。该算法的关键思想是一种基于像素的概率深度估计方案，可以随着每个新帧来更新后验深度分布。目前的实现能够每秒更新 1500 万个深度分布。我们将所提出的方法与最先进的实时 MVS 方法进行评估，并显示了在精度方面的改进。

1. Introduction

近年来，双目和多视角立体（MVS）研究已经达到了一定的成熟水平，可以轻松地对各种场景进行高质量的重建结果 [23, 26]。然而，将 MVS 方法应用于视频流的可能性却受到了较少的关注。视频流的基于实时 MVS 系统是静止图像系统的有趣替代方案的原因有几个。对于小规模重建，视频采集可能比获取静态图片更快速、更用户友好，例如快速原型制作或工业建模。同样，对于非常大的场景重建，例如城市范围的 3D 模型，需要大量数据，视频可以提供一种价格合理、易于使用的捕获海量数据的方式。由于大规模重建算法非常需要数据，因此使用它们的两种主要范式是视频 [6, 22] 或社区照片收集 [1, 21, 24]。照片收集具有不断更新的巨大优势。主要缺点是目前只能用于旅游地点，如罗马的斗兽场或杜布罗夫尼克市，而手持相机可以随时用于重建任何感兴趣的场景。从算法的角度来看，视频具有几个与静态图像捕获有所不同的特点。

首先，与静态图像相比，数据质量通常较低，包括图像分辨率、运动模糊或压缩伪影等问题。其次，数据量比静态图像序列大几个数量级。大多数表现最佳的多视角立体视觉（MVS）技术在处理相对较小的视频序列时无法处理内存和计算时间方面的问题。然而，庞大的数据量也是优势之一，因为它解决了许多由重复纹理、无纹理区域或遮挡引起的 MVS 中固有的不确定性。这与通过计算昂贵的规则化来解决 MVS 中的不确定性的传统方法形成对比。最后，连续帧之间的基线很小，这意味着图像流仅限于相邻帧之间的几个像素。因此，寻找对应关系更容易，因为需要搜索的图像位置更少。

在本文中，我们提出一种算法，利用视频输入的优势，同时又能够应对它所面临的挑战。我们描述的系统在任何时刻都维护一个大型候选 3D 特征集合（约 250,000 个）。它具有它们的 3D 位置的估计值，并随着每个新进来的帧而改进。当对这个估计值的置信度足够高时，候选 3D 特征就会被整合成一个 3D 点，并离开候选池，同时引入一个新的特征。这种策略的关键要求是：

顺序更新方案以在获取视频帧时获得中间 3D 估计值，
精度度量以确定 3D 估计值的准确性，
异常值拒绝方案可靠地拒绝由于遮挡、缺乏纹理等原因在 MVS 中出现的异常值，
计算效率高，内存占用低。
一种满足前三个要求的优雅框架是概率推断 [16]。在本文中，我们提出了一种新颖的**参数化贝叶斯近似方法**，符合上述所有要求，包括计算速度极快，内存占用极低（每个 3D 特征使用 9 个浮点数来模拟位置，加上 25 字节的参考图像补丁patch）。

本文的主要贡献包括：

针对遮挡鲁棒的概率一致性方法 [13] 的概率处理，
对完整的概率推断问题进行参数化近似，从而使实时贝叶斯 MVS 问题可行，
展示了一种基于视频的 MVS 系统，能够在处理视频输入时实时（60Hz）工作，并提供中间重建结果作为用户反馈。

2. Previous work

本文主要涉及多视角重建（MVS）领域的文献，同时也与实时姿态和场景重建相关。我们首先引用[23]中的MVS评估结果。从评估中表现最好的算法中可以分为两个主要趋势：区域生长方法[8、11、12、20]和鲁棒性强的光度一致性方法[3、5、10、13、18、27]。表现最优秀的区域生长方法[8]结合了基于光度一致性的块匹配、扩展和过滤等步骤来重建感兴趣的场景。这种方法成功的原因是基于**平面的光度一致性在低纹理区域或稀疏数据集上效果非常好**。然而，在视频环境下很难将补丁生长步骤转化到该领域。这是因为当一个补丁被优化并且必须在其附近生成新的补丁时，摄像头已经移动到了其他区域。因此，算法必须将之前的图像保留在内存中，这在每秒30-60帧的长序列中是不可行的。或者，系统必须等到摄像机重新访问补丁，这使得它难以在驾车场景中使用（例如，汽车上安装的MVS系统重建城市的部分区域）。

鲁棒性强的光度一致性方法提供了一个非常简单的流程，使用像密集立体和三维分割等成熟算法。然而，它们依赖于一个更简单的基于窗口的光度一致性，对稀疏图像和缺乏纹理的情况不够鲁棒。在这个群体中表现**最好的算法[13]通过直方图投票估计深度局部极大值。然而，在实时视频环境中，使用直方图进行深度估计存在以下困难**：(a) 随着新帧的获取和直方图更新，不清楚如何测量当前深度估计的置信度。(b) 估计精度取决于条带大小。© 直方图往往需要占用大量内存。我们的方法受到这个第二组方法的启发，并提出了面向遮挡鲁棒性的光度一致性的概率解释。我们推导出对后深度分布的参数近似，克服了直方图方法的困难：(a) 概率框架为计算的估计提供了置信度度量，同时(b) 估计不是量化的。最后，© 我们**对深度后验概率的表示具有较低的内存占用。

我们的工作也与实时城市重建方法[6、22]相关。虽然[6]假设建筑物的形状模型非常简单，但[22]的方法可以用于重建一般的三维场景。与他们的方法相比，主要区别在于对摄像机运动的鲁棒性和精度改进。他们算法的核心是每0.5秒产生一个密集立体深度图，使用该时间段内捕获的帧。然后将深度图与先前生成的结构在3D中融合，解决可能出现的任何不一致性。这个系统在车载摄像头上效果非常好，因为摄像机的运动是平滑且速度变化缓慢的。如果摄像机的基线太小（车停下来）或太大（车速太快），该系统将丢失这些帧。这使得他们的算法不太适合手持交互式MVS，而我们的目标是这个领域，其中摄像机运动通常不平稳。相比之下，我们的表达方式与摄像机运动类型无关。只有在达到一定的置信度和3D精度时才会生成几何体的每个部分。这意味着具有良好焦点和足够基线的给定部分可以在几个十分之一秒内生成，而其他部分可能需要更长时间，例如被遮挡的区域或摄像机运动不稳定的区域。

本文还与视觉SLAM [7]具有类似的地方，我们都是顺序更新一组3D特征。主要区别在于，我们的目标是最大化3D特征的产生，并假设摄像机姿态估计已知，因此可以利用极线几何。最后，一些文献[2、4、9、14、25]中也提出了面向概率MVS的方法。然而，虽然这些方法明确地对遮挡进行建模，但我们的方法假设不同像素深度之间具有概率独立性，并将遮挡隐含地建模为另一种噪声源。这个独立性假设是使实时MVS问题可处理的关键因素，我们相信我们的实验结果在实践中证明了这一点。

3. Probabilistic depth sensor

假设p是已校准的图像I的像素，具有位姿和内部相机参数。对于特定深度值Z，可以获得相应的3D点x（Z），该点位于沿着p的光学线从I开始Z个单位的距离处（参见图1）。
设I’是从附近视点获取的另一个已校准图像，W和W’分别表示以3D点x（Z）在I和I’上的投影为中心的两个正方形补丁。我们可以使用归一化交叉相关（NCC）在3D位置x（Z）处评估照片一致性[19]。 图2显示了沿着深度的单个像素的NCC分数以及这些曲线的局部最大值的直方图，其中包括60个相邻图像的最大值。
(简述：左图是该特征点在一幅图像上面的匹配，随着Z的变化，对应在极线上的不同投影点位置。该特征点图块经过仿射变化之后，与不同的投影点位置的图块进行NCC匹配，获取不同的匹配分数，然后记录极大值点，落在哪个Z值区间。从Zmin到Zmax分了50段区间。右图是把60幅图像这样的数组累加，把极大值点累加，记录在每个Z值区间出现的极大值的频数。)

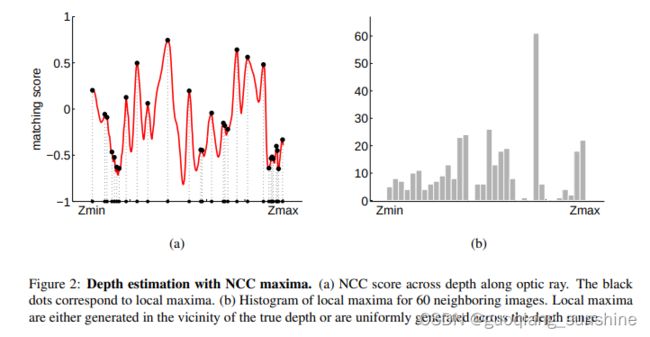
图2：NCC最大值深度估计。（a）沿视觉光线的深度NCC得分。黑点对应于局部最大值。（b）60个相邻图像的局部最大值直方图。局部最大值要么在真实深度附近生成，要么在整个深度范围内均匀生成。

我们观察到，直方图集中在单个模式上，对应于真实深度，并且具有均匀成分，对应于遮挡、图像扭曲、重复纹理等因素。这种情况表明概率分布是好测量和坏测量模型之间混合的结果。好测量模型将几乎所有的概率质量都放置在正确的深度位置周围，而坏测量模型在所有可能的深度位置均匀分布其质量。接下来的章节将详细解释这一点。
简述：一幅图像中的像素点为中心产生一个patch，在另一幅图像对应的极线上搜索patch，使用NCC（NormalizedCrossCorrelation）来分析两个patch间的相似程度，在深度[X(min),X(max)]区间内进行搜索匹配，这个区间内NCC的计算结果会产生一系列局部极值。把上述计算过程看作是一个深度传感器的计算过程，其输出结果为一系列NCC的局部极值对应点的深度信息。但是它们是有噪声的数据。一幅图像对应另外n幅图像，可以看作为n个深度传感器，把得到点的深度信息的问题看作是有噪声的多传感器数据融合的问题，使用**GaussianUniform mixturemodel来对这一问题进行建模，假设好的测量值符合正态分布，噪声符合均匀分布，好的测量值的比例为pi，使用贝叶斯方法不断更新这个模型，让点的深度（也就是正态分布中的均值参数）和好的测量值的比例pi收敛到真实值**。

（简述：这种方法比较准确，但是需要记录大量的数据。比如上面（a），单是一幅图上，从Zmin到Zmax就分了50段，于是要用50个元素的数组来记录每段有无极大值。然后把60幅图像的数组都合并起来得到（b）。而且，即便能知道累加后最高的那个直方图对应的深度值，但不能知道根据所有的测量结果所推算出来的深度值，也不知道那个特征点对应的外点（假地图点）的概率。）

实际实现的时候一个seed对应与图像中一个像素，这个像素是想要求得其深度信息的点。
一个seed还关联五个参数，其中四个参数是模型中的参数，分别是好的测量值和坏的测量值的个数，深度估计中高斯分布的均值和方差。最后一个参数是以这个像素点为中心的一个正方形patch，计算这个patch和其他图像中的对应极线上的patch的NCC值，此处因为计算量的关系不会搜索整个极线，只会搜索以目前模型中高斯分布的均值（深度）对应的极线上的像素点为中心的一个固定范围。

每次新进一帧，依照这样的过程：
1.产生新的seed（seed的数目固定，上次迭代结束时会去掉一些seed）
2.对每个seed进行更新：在此帧上进行相关seed的对极搜索；检测极线上点对应patch与seed中的patch的NCC分数的局部极大值；用这些局部最大值更新seed中的四个参数
3.去掉那些好的测量值的个数低于阈值的，如果好的测量值的个数高于阈值而且方差低于一个阈值，把这个seed对应的点的三位坐标算出来并加到地图中。

我们将局部最大值x1，…，xN视为来自深度传感器的一组嘈杂测量。我们将传感器建模为一个混合分布，将良好的测量模型与坏的测量模型混合在一起，这是强健传感器融合问题中常见的情况（例如[16]第21章）。我们的传感器可以以概率$\pi$和$1-\pi$产生两种类型的测量：
（1）围绕正确深度Z的正态分布的好测量；
（2）从区间$[Z_{min}，Z_{max}]$中均匀选择的异常值测量。限制Zmin和Zmax可以通过对场景几何形状的某些先验知识进行确定。感兴趣的对象保证完全包含在$[Z_{min}，Z_{max}]$之间。以下高斯+均匀混合模型描述了给定正确深度位置$Z$和内点概率$\pi$的第$n$个测量的概率分布。

$p(x_n|Z,\pi )=\pi N(x_n|Z,{\tau }^2)+(1-\pi )U(x_n|Z_{min},Z_{max})(1)$
其中，$\mathcal{N}$表示正态分布，$\mathcal{U}$表示均匀分布，$Z_{\min }$和$Z_{\max }$表示先验知识确定的深度范围的下限和上限，${\tau }_n$是第$n$个测量的噪声方差。
好的测量方差${\tau }_n^2$可以通过产生该测量的$I$帧和$I^{\prime }$帧相机的相对位置来获得。这是因为我们假设当在$I^{\prime }$中投影时，测量$x_n$具有一个像素的固定方差。然后，我们将这个方差反向投影到三维空间中，以计算测量的距离单位的方差。

3.1 贝叶斯推断

式（1）中引入的似然函数是典型的混合模型，因此可以在最大似然框架下使用期望最大化算法从数据$x1,...,xN$中估计其参数。然而，重要的是要对我们的深度估计有一个置信度度量，因为它可以用来在收集足够的测量时通知系统，并检测估计是否失败。最大似然方法无法提供这种度量。此外，在我们的实验中，期望最大化算法在相当多的情况下陷入了局部最优解。因此，我们选择了贝叶斯方法，其中我们定义了深度和内点比率的先验分布，然后计算给定所有测量的后验分布。估计的深度是该后验分布的最大值，其形状（通过二阶矩）确定了我们估计的置信度**。（简述：引入贝叶斯方法,建立深度和内点比率的先验分布，通过更新多次测量，更新给定所有测量的后验分布，得到估计的置信度）

假设所有测量$x1，...，xN$是独立的，后验分布具有以下形式：

$p(Z,\pi |x1,...,xN)\propto p(Z,\pi ){\prod }_{n}p(x_n|Z,\pi )(2)$

其中，$p(Z,\pi )$是深度和内点比率的先验分布，${\prod }_{n}p(x_n|Z,\pi )$ 是似然函数（式（1）中的表达式）。该公式表示给定**所有测量值$x_1,...,x_N$时深度$Z$和内点比率$\pi$的后验概率密度函数。
（后验分布=先验 * 似然）
下图参考《视觉SLAM十四讲》13.2.3的《高斯分布的深度滤波器》。这里的都是指概率密度。${\tau }_n$是匹配点在极线上的一个像素的扰动，造成的对应点在深度上的变化。

图3第一行展示了在收集测量值时 $p(Z,\pi |x_1...x_n)$ 的演变过程。假设先验是均匀的，并且使用密集的二维直方图对分布进行建模。后验收敛于正确的深度$Z$和内点比率 $\pi$ 的值。在第5节描述的实验中，我们展示了这种概率形式优于[13,27]中使用的直方图投票方法，并在表1中进行了总结。

图3：后验分布的非参数化与参数化建模。
第一行展示了以二维直方图的形式进行非参数化建模的后验分布。四列代表四个时间实例（5、10、20和100次更新后,简述：随着观测的增加，后燕概率收敛的过程）。
第二行展示了我们参数化的高斯×Beta近似的演变过程。尽管我们的模型无法捕捉真实后验分布的多峰性质，但几次迭代后，它收敛于相同的点估计值。简述：实验证明这个是一个凸优化问题，收敛在局部最值上。
第三行显示系统在每个时间实例中所看到的测量值的直方图。最后三行显示了少数几种情况，其中参数化模型无法跟随非参数化模型。当发生这种情况时，可以检测到，因为参数化后验预测非常低的内点比率。因此，我们可以安全地将其丢弃。x轴表示所有图像沿光学射线的深度。

然而，由于内存和计算限制，为每个像素建立完整的2D直方图来建模后验不切实际。我们的系统同时保持着250,000个种子。一个合理的2D直方图应该至少用500个值来量化深度和100个值来量化内点比率。为了将这些直方图保留在内存中，我们需要存储125亿个浮点数（非常复杂!）。此外，即使使用GPU实现，也无法实时更新完整的2D直方图。我们的方法是使用参数近似来逼近后验分布，下面将对此进行概述。

3.2 参数化后验的近似

当种子对应于纹理良好、未遮挡的像素时，深度观测的直方图具有单一的模式（见图5a）。这促使我们使用单峰参数后验的方法。深度后验（4）的一个较好的近似是将深度的高斯分布与内点比率的Beta分布相乘。在补充材料中，我们提供了该形式的变分论证。特别地，我们展示了它与真实后验之间的Kullback Leibler散度最小，而其他可能的近似分布则共享弱因子分解属性。因此，我们将Eq. (2)的后验近似定义为：
$$q(Z,\pi |a_n,b_n,{\mu }_n,{\sigma }_n):=Beta(\pi |a_n,b_n)N(Z|{\mu }_n,{\sigma }_n^2)（3）$$

其中，$Beta(\pi |a_n,b_n)$表示Beta分布的概率密度函数，$N(Z|{\mu }_n,{\sigma }_n^2)$表示正态分布的概率密度函数。$a_n$和$b_n$可以被看作是种子在其生命周期内发生了多少个内点和外点的概率计数器。另外两个参数${\mu }_n$和${\sigma }^2$表示我们高斯深度估计的均值和方差。现在，如果$q（Z，\pi |a_{n-1}，b_{n-1}，{\mu }_{n-1}，{\sigma }_{n-1}^2）$是n - 1次测量后的真实后验，观察到$x_n$后的新后验将具有以下形式：
$C\times p(x_n|Z,\pi )q(Z,\pi |a_{n-1},b_{n-1},{\mu }_{n-1},{\sigma }_{n-1}^2)（4）$

其中，$p(x_n|Z,\pi )$表示给定隐变量Z和π时，$x_n$的似然函数；$q(Z,\pi |a_{n-1},b_{n-1},{\mu }_{n-1},{\sigma }_{n-1}^2)$表示给定先验超参数$a_{n-1},b_{n-1},{\mu }_{n-1},{\sigma }_{n-1}^2$时，隐变量Z和π的后验分布。C是一个归一化常数。

因此，该分布不再具有高斯×Beta的形式，但我们可以使用矩匹配来近似它。因此，我们定义新参数$a_n{b}_n{\mu }_n{\sigma }_n^2$，使得（4）中的乘积和我们对真实后验$q（Z，\pi |a_n，b_n，{\mu }_n，{\sigma }_n^2）$的近似在Z和π的一阶和二阶矩上相同。这个更新可以通过解析计算得到，但我们将读者引导到补充材料中查看实际的公式。图3的第二行和第五行展示了参数化后验随着贝叶斯更新而演变的情况。即使我们的近似是单峰的，而真实后验不是，它几乎总能收敛到相同的Z和π的值。在极少数无法收敛的情况下（图3的第五行），该分布会给予非常低的内点比率很高的概率。当发生这种情况时，我们可以确信估计已经失败，我们可以忽略结果。

图4展示了具有参数化近似的这种贝叶斯更新的典型演变。Z和π的估计值（图4a和b）收敛于正确的值，可以通过将测量直方图与边缘化的测量后验 $p（x|x_1，...，x_n）$叠加在一起来看出（图4c）。

图4：参数更新演化: 前两个图显示了深度估计Z和内点概率π的演化。我们显示平均值±两倍标准差。第三个图显示了测量直方图，同时叠加了测量后验概率$p（x|x_1，...，x_n）$。均值和离群值水平都被正确捕获了。

重要的是要注意，估计问题的成功或失败也取决于参考块(patch)W的观测质量，在传感器深度后验的演变过程中保持不变。如果该块纹理良好并在随后的帧中可见，则通常可以成功估计。另一方面，如果像素区域没有纹理或在随后的帧中被遮挡，则估计将失败。
重要的是，这些失败情况可以被检测出来，因为估计的内点比率非常低。这些情况在图5 b和5 c中显示。

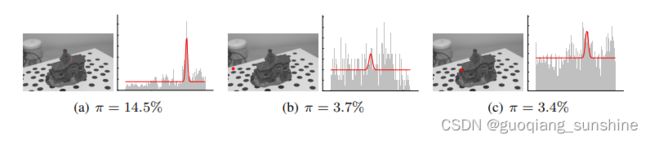
图5：三种像素传感器类型。这些图显示了三种像素传感器的测量直方图和叠加的测量后验概率p(x|x1,…,xm)。在（a）中，像素是物体上纹理明显的点。在（b）中，像素对应于完全没有纹理的白色点。在（c）中，像素对应于将在接下来的几帧中被遮挡的点。估计的内点比率在三种情况下都显示出来。两个病态案例，（b）和（c），可以从它们的低内点比率中识别出来。

4. System details

本文的目标之一是评估基于视频的多视角立体算法的可行性和可用性。在本节中，我们描述了一个基于前面描述的思想的实时重建系统的实现。该系统是一个基于CUDA的混合CPU/GPU实现。它可以在Intel XEON 2.33GHz和NVIDIA GTX 260上每秒更新250,000个种子60次。我们还在装有NVIDIA GTX 280M芯片组的双核笔记本电脑上实现了便携式版本。可移植版本每秒更新250,000个种子30次。

4.1 相机姿态估计

近年来，视觉SLAM技术取得了重大进展。最新研究参考文献可见[7,17]。这些方法可以从刚性场景的视频序列中的点和线特征中跟踪相机的6自由度运动。然而，在本文中，我们的目标是独立于基于SLAM的相机跟踪器中的任何不准确性评估密集的3D结构估计。为了实现这一目标，我们选择了一种简单但非常准确的基于模板的相机跟踪方法，使用[28]。这种技术包括每帧捆绑调整阶段，可以获得小于0.05像素的重投影误差。

4.2. 种子的演化

该系统执行视频序列中各个像素深度的顺序推理。一个种子对应于一个特定的像素p，我们的目标是估计其深度。。由于存储和计算限制，我们可以在整个过程中维护一定数量的固定种子。每个种子都与一组参数值$（a_n、b_n、{\mu }_n、{\sigma }_n^2、W）$相关联。种子生命周期中发展的前四个参数描述了我们根据公式（3）对前n次观测得出的后验概率。对于每个种子，我们还在参考图像$I$上种子像素位置周围存储一个参考图像块W。该块保持不变，并用于与目标图像进行比较并获取深度测量值。创建种子时，我们设置$a_0=10$和$b_0=10$。这对应于以0.5为中心和标准偏差约为0.1的内点比率先验。深度参数${\mu }_n$和${\sigma }_n^2$被设置为使得先验概率质量的99％在某个预设的$Z_{min}$和$Z_{max}$之间。这些参数的设置定义了一个包含感兴趣物体的边界体积。

在种子的生命周期内，我们通过评估存储块$W$和当前帧$I^{\prime }$上极线上的块$W^{\prime }$之间的NCC来获得深度测量值（参见图1）。理想情况下，我们希望在NCC得分的整个极线上搜索局部最大值，但这在普通硬件上不可行。相反，我们利用小的帧间运动，仅在距离先前均值$µ_n$投影处$w$像素半径内进行搜索。这违反了等式（2）的独立性假设，因为先前的测量现在将决定新测量的搜索区域。尽管如此，在实践中这种近似方法效果很好。在真实深度超出极线搜索窗口的情况下，种子将产生错误的深度测量。我们依靠内点比率估计来检测来自该种子的测量是否为异常值。然后，该种子将被丢弃，如下一节所述。在本文中展示的实验中，对于我们的200万像素摄像机，w设置为3像素。在未检测到局部极大值的情况下，通过设置$b_{n+1}：=b_n+1$对种子进行惩罚。这具有观察到已知为异常值的深度测量的效果。

Alg.1算法：一种基于视频输入的多视角立体匹配（MVS）方法，用于估计场景的三维结构。该算法维护一组“种子点”，最初是根据视频的第一帧生成的，并随着新帧的处理而不断优化。

该算法对于每个新帧如下进行处理：

1. 如果系统中的种子点数量少于M，则在当前帧上生成新的种子点。
2. 对于每个种子点：
   a. 投影种子点到当前帧以获取光线方向。
   b. 在投影光线周围的搜索窗口内查找具有最高归一化互相关（NCC）得分的像素位置。
   c. 使用检测到的像素位置处的NCC得分更新种子点的后验深度分布。
3. 删除任何具有少于指定阈值ηoutlier的内点比率的种子点。
4. 将任何剩余的内点比率高于指定阈值${\eta }_{inlier}$且后验方差${\sigma }_n(<ϵ)$ 较小的种子点转换为三维点，并从种子点列表中删除它们。

该算法通过时间迭代地优化种子点的深度估计，舍弃不可靠的种子点并将可靠的种子点转换为三维点。维护足够覆盖场景的种子点数量和删除不可靠种子点之间的平衡由最大种子点数M和内点比率阈值${\eta }_{outlier}$和${\eta }_{inlier}$控制。

4.3 种子修剪

在前面描述的种子演化步骤之后，有三种可能的结果：
• 种子已收敛到一个良好的估计值，因此将其从种子列表中移除，并在当前后验均值${\mu }_n$处生成3d点。
• 由于存在过多的异常值，种子未能收敛。然后从列表中删除该种子。
• 种子还没有被充分收敛，因此它将存活到下一个演化步骤。
为了确定适当的结果，我们使用深度后验方差σ²n和估计的内点概率π。我们采用以下标准：

1. 如果根据当前的后验分布$q（Z，\pi |a_n，b_n，{\mu }_n，{\sigma }^{2}n）$，内点比例$\pi$小于99%的${\eta }_{outlier}$，则我们可以得出结论认为深度估计失败。这通常是在种子初始化在焦点之外的图像补丁上，或者后续图像中没有足够的纹理匹配时发生的情况。
2. 如果我们的后验均值内点比例大于${\eta }_{inlier}$且深度方差${\sigma }_n<ϵ$，则我们假设深度估计成功。
3. 在所有其他情况下，我们让种子进一步演化。
   在我们所有的实验中，阈值参数都被固定为${\eta }_{outlier}$= 0.05，${\eta }_{inlier}$ = 0.1。方差阈值$ϵ$设置为$Z_{max}-Z_{min}\ast 1/10000$。生成的3D点被收集到一个八叉树结构中，并以实时Z-buffer shading着色的方式进行图形渲染。Alg.1提供了我们方法的摘要。

补充：Z-buffer shading 是一种计算机图形学中的渲染技术，其基本原理是在三维场景中确定每个像素与相机之间的距离（即深度值）并将其存储在一个称为 Z-buffer 的缓冲区中。当完成深度值的计算后，便可以用它来决定哪些像素应该被渲染，以及哪些像素应该被遮挡。

在进行 Z-buffer shading 时，首先需要定义场景中的所有物体及其位置和大小。然后，在绘制每个像素之前，都会检查其深度值与 Z-buffer 中已有的值进行比较。如果该像素的深度值小于或等于 Z-buffer 中已有的深度值，则说明该像素不会被遮挡，可以被渲染出来；否则，该像素将被遮挡，并且不会被渲染。

5. Evaluation

图6：与实际情况的比较。我们的算法在一个玩具房屋的600帧视频序列上与[22]进行了比较。(a)房屋的实际模型。(b)[22]的结果。©我们在整个600帧上的结果。(d)我们方法在每20帧上运行的结果(总共30个输入图像)。与[22]相比，我们的结果更加详细，但是特别是在30帧的情况下，不够完整。这是因为我们的方法缺乏任何空间正则化，而且[22]生成网格，而我们的结果是3D点云。这些结果的完整性-精度曲线可以在图7中找到。

图7：实际情况实验的准确性和完整性曲线。(a)展示了我们算法在一个房屋视频序列的30帧和600帧上的准确性结果。该图显示了在给定距离d下，重建模型中有多少部分在实际模型的d范围内。(b)测量完整性。即在距离d范围内，实际模型有多少部分在重建模型的d范围内。我们的结果更加准确，但是稍微不够完整。这是因为我们的方法没有执行正则化并返回未网格化的点云。

5. Conclusion

本文介绍了一种基于独立像素深度估计的视频多视角重建（MVS）方法。我们在极线上寻找相关性得分的局部最大值，并在概率框架内融合这些候选三维位置。我们的实现处理每秒60帧的2兆像素视频，能够在提供用户在线反馈的同时准确重建小物体。我们的方法经过与地面真值的验证，发现可以产生精确的重建结果，并且随着输入数据量的减少而逐渐降低精度。
本文的目的之一是展示基于视频的实时MVS系统的可用性，这些系统通过中间结果提供在线反馈。为达到这个目的，我们展示了如何在几秒钟内获取各种物体的3D模型。另一个目的是评估视频数据在没有任何正则化的情况下解决MVS中的歧义的能力。我们的结果显示，与有正则化的方法相比，我们的方法在精度上有所提高，但在完整性方面有所降低。
我们认为，基于视频的MVS系统在快速获取采集时间的情况下，具有重建大规模模型的巨大潜力。这是因为它们提供的物体覆盖范围比静态照片更密集，而在线反馈有助于避免昂贵的返回场景。在未来的工作中，我们打算在户外部署我们的方法，并将其应用于大规模场景的重建。

6. reference

https://publications.aston.ac.uk/id/eprint/19671/1/hernandez_imavis2011.pdf
https://www.cnblogs.com/ilekoaiq/p/8228324.html