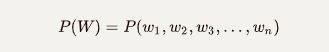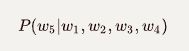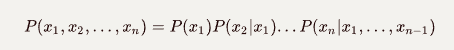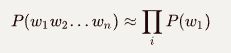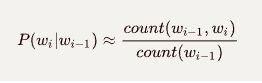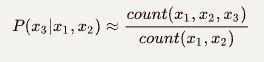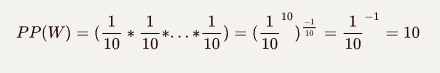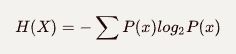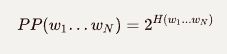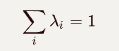NLP语言模型(LMs)在实际数据中的应用
语言模型(LM)的作用是估计不同语句在对话中出现的概率,并且LM适用于许多不同的自然语言处理应用程序(NLP)。 例如,聊天机器人的对话系统。
在此文中,我们将首先正式定义LM,然后演示如何使用实际数据计算它们。 所有显示的方法在Kaggle notebook中有完整的代码展示。
一、语言模型(LM)的定义
概率语言建模的目标是计算单词序列的语句出现的概率:
或者预测下一个词出现的概率:
实现上述功能的模型称之为语言模型(LM)
计算概率的一般方法
条件概率的定义
假设A和B表示两个事件并且P(B)≠0,给定B的条件下,A概率为:
链式规则的定义
一般情况下,链式规则的公式如下:
链式规则用于计算单词序列的语句中的联合概率:
举例来说:
这需要有大量的计算工作,并且不能通过计数和除以条件的方式来完成比如:
一般来说使用这种方法是不可行的,因为有很多可能的句子需要计算,并且存在非常稀疏的数据使得结果不可靠。
马尔科夫假设的方法
马尔科夫特征的定义
如果随机过程的未来状态的条件概率分布(以过去和现在状态为条件)仅取决于前k个状态,而不取决于其之前的所有状态,则称随机过程具有马尔可夫特征。 具有此特征的过程称为Markov过程。
换句话说,只需要给出前k个词,可以估计下一个词的概率。
例如 if k=1
if k=2
马尔科夫假设的一般公式为当k=i时
N-gram 模型
基于Markov假设,我们可以正式定义N-gram模型,其中k = N-1如:
这个公式的最简单版本是Unigram模型(k=0)和Bigram模型(k=1)
Unigram 模型 (N=1,k=0):
Bigram 模型 (N=2,k=1)
N-gram该模型还可以被扩展到Trigrams(3-gram), 4-grams, 5-grams等。这是一种不充分的语言模型,因为句子通常具有长距离依赖性。 例如,句子的主语可能在开始的位置,而我们要预测的下一个单词出现在10个单词以后。
估计Bigram的概率使用最大似然估计的方法
一个简单的例子:
给定一个语料库包含3个句子,我们要计算以字母“I”开头的句子的概率:
其中 表示句子的开始符号和结束符号
因此我们有:
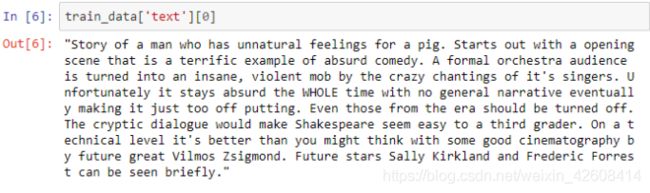
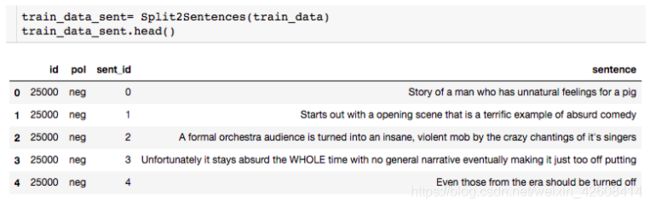
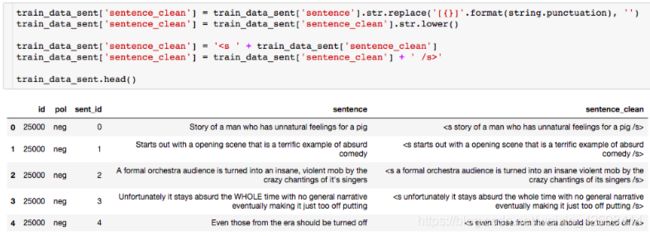
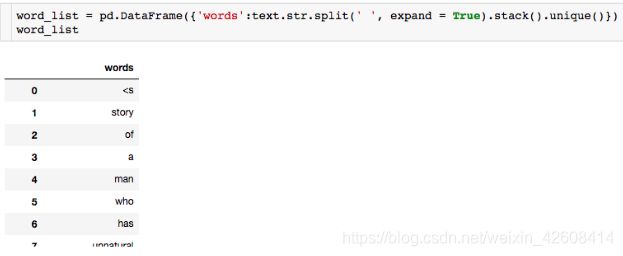
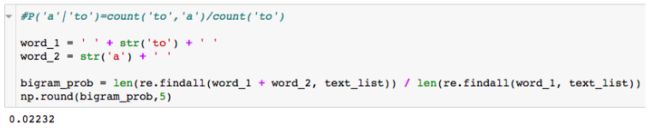
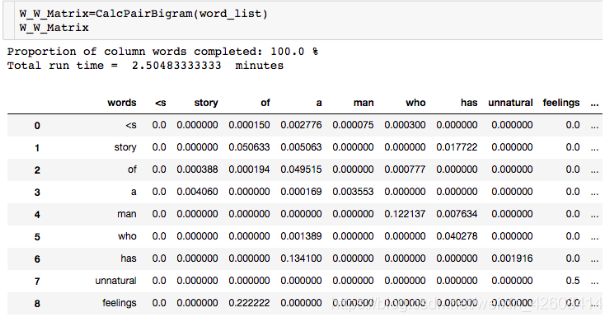
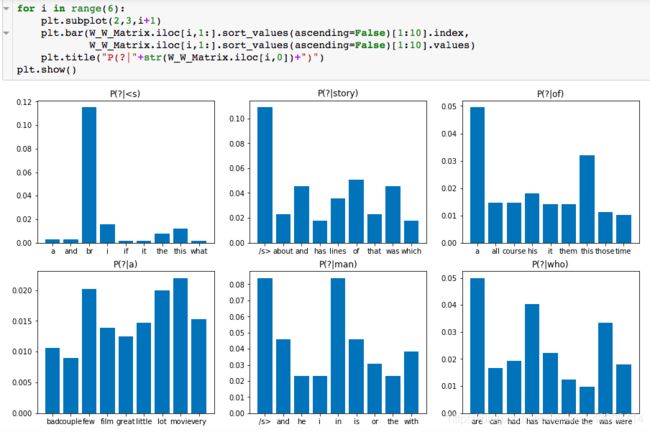
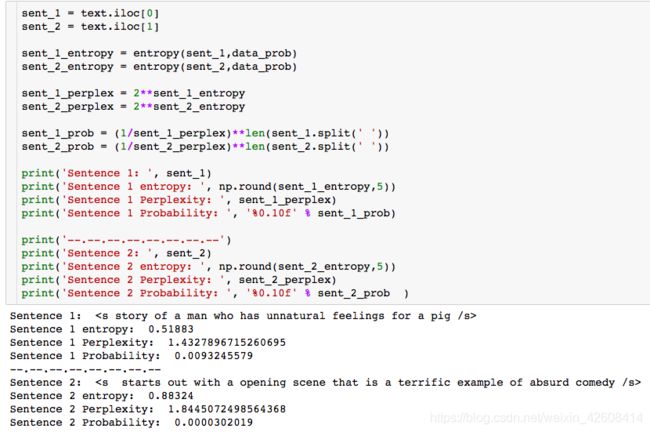
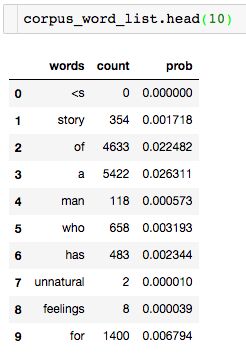
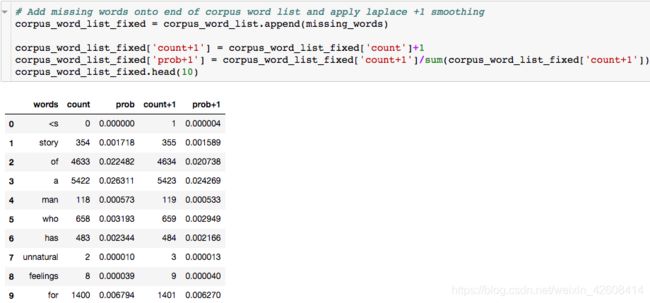
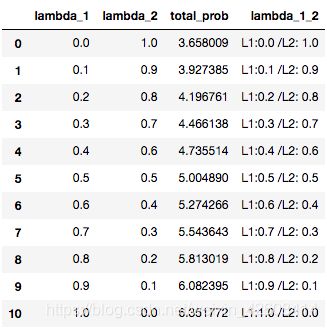
很明显,在我们的语料库中 在本次演示中,我们将使用斯坦福大学提供的IMDB大型电影评论数据集。 数据包含评论者给出的评级、正负倾向以及完整评论。 例如,这里的第一个负面评论如下: 我们注意到到每条评论都是由若干个单独的句子(由句号分隔)所组成,接下来我们要做的是分句:将所有评论中的句子拆分出来形成一个新的数据集: 接下来要做的工作是数据清洗:删除标点符号,字母小写化,加入句子开始符结束符. 接着要做的是数据整理:将所有句子合成为一个巨大字符串 然后是最关键的一步:创建此词汇表 有了词汇表以后,我们可以计算出每个词的词频和概率: 到此为止,数据的预处理工作基本完成。 由于这是最容易计算的,我们可以找到每个单词出现的概率,用它来计算整个句子发生的概率,如: 我们还可以使用另一种常用的计算方法是采用对数概率: 之所以要使用对数概率的方法是因为使用加法比使用乘法速度更快。 例如,对于unigram模型,我们可以计算以下单词的概率。 unigram模型可能不准确,因此我们引入了bigram模型。 使用这个模型稍微复杂一些,首先我们要从单词的同现矩阵中找出单词每个单词的同现单词(两个单词同时出现) 。 然后通过前一个单词的计数并对计数进行归一化,如下面的等式所示: 例如,如果我们想要改进先前的P(a | to)的计算,我们首先计算 (to,a) 的同时出现次数并将其除以 (to) 的出现次数: 另外,我们还可将原来的单词 to 改成 has: 如上所述,为了正确使用bigram模型,我们需要计算所有“单词对”的同现概率矩阵。 有了这同现概率矩阵,我们可以找到最有可能跟随当前词的其他词。 然而,如果语料库很大,这也需要非常长的时间。 有了同现概率矩阵,我们可以找到一些关于跟随给定单词的最可能的其他单词的例子: 从上图可知跟随 有些词可能会有很多可能的跟随词,但有的词如“unnatural”只有一个跟随词,这可能是由于生活中很少有词语跟随“unnatural”一起出现吧。 可以利用以下公式将N-gram模型扩到Trigram: 例如: 通过上述计算我们发现“to a movie”比“to a film”更为常用! 由于训练LM的语料库会影响预测的输出结果。 因此,我们需要引入一种方法来评估经过训练的LMs的表现。 受过最好训练的LM能够在没有见过的测试集中正确预测下一个句子中的下一个单词。 这可能非常耗时,因此构建多个LM进行比较可能需要数小时才能计算出来。 因此,我们引入了内在评估方法:perplexity(复杂度)的。 简而言之,perplexity是衡量概率分布或概率模型预测样本的好坏程度。 perplexity是衡量语言模型好坏的指标,它是由单词数量normalize的测试集的逆概率,更具体地说,可以通过以下等式定义: 例如 假设一个句子由随机数字[0-9]组成,如何计算这个句子的perplexity? 假设该模型为每个数字赋予相等的概率(即P = 1/10) 在信息理论中,随机变量X的熵(表示为 H(X))是期望对数概率: 熵是用来衡量不确定性指标,换句话说,熵是系统可能的状态数。 示例:抛一枚质地不均为的硬币的熵计算: 假设硬币正/反面朝上的概率定义为: 那么我们可以计算出它的熵: 通过改变硬币的概率,我们可以得到所有熵的分布: Perplexity(复杂度) 和 Entropy(熵)的关系 这个式子可以这样理解,Perplexity越小,P(wi)则越大,我们期望的句子出现的概率就越高。 可以通过Perplexity(复杂度) and Entropy(熵)的关系计算出整个句子的概率,过程如下: 1. 计算句子的熵 2. 计算句子的perplexity 3. 计算整个句子的概率 完整代码过程如下: 由上述计算结果可知Perplexity越高,句子的出现的概率越低。 由于LM的输出结果依赖于基于训练集的语料库,因此如果训练集的语料库与测试数据集类似,则N-gram可以很好地工作,但是我们在训练中存在过拟合的风险。 与任何机器学习方法一样,我们希望模型在新的数据集上工作良好。更难的是我们如何处理那些没有出现在训练集的语料库中但是却出现在测试数据集中的单词。 为了处理那些在测试集中出现但在训练集的语料库中未出现的单词,我们可以引入Laplace +1 的平滑操作。 为此,我们只需为每个未出现在语料库中的单词的计数+1。 首先我们抽取原始训练集中的90%的数据作为新的语料库,同时将剩下的10%的数据作为测试集,并计算词频和概率 然后我们找出那么在测试集中出现,但在新的语料库中未出现的单词,并将这些单词合并到新的语料库中去,并将这些单词的计数有原来的0置为1,然后再计数这些单词的概率。 最后我们可以看到在使用Laplace +1平滑之前和之后单词计数的分布情况: 这略微改变了概率分布,并且经常用于文本分类和未出现单词数量不大的情况下。 但是,这通常不用于n-gram模型,因为还有一些更复杂的方法。 Laplace +1平滑用于文本分类和未出现单词数量不大的情况。 然而,它通常不用于n-gram模型,对于n-gram模型来说还有的一些更好的平滑方法: 我们已经介绍了前三个LM(unigram,bigram和trigram)但哪个最好用? Trigrams通常比bigrams有更好的预测结果,而bigrams比unigrams有更好的预测结果,但随着复杂性的增加,计算时间变得越来越长。 此外,随着单词数量N的增加,预测下一个单词的数量会减少(如10-gram中预测下一个单词比bigram模型少得多)。 除非有好的证据表明使用trigrams(或更高的n模型)会得到更好的预测结果,那么请使用trigrams(或更高的n模型),否则请使用bigrams(或其他更简单的n-gram模型). 在插值法中,我们使用混合n-gram模型。 简单插值法: 其中 一个简单的例子 例如有以下语料库: 我们使用基于Bigram和Unigram的混合n-gram模型,设λ1=1/2, λ2=1/2,求P(Sam | am)的概率(注意:计算时需要包括 可以使用如下公式: P(w2 | w1) = λ1×P(w2 | w1)+P(w2) 因此我们有: 其中: 最后我们得到: 我们应用如下公式: P(w2 | w1) = λ1×P(w2 | w1)+P(w2) 并且使用之前从IMDB数据集定义的语料库,我们将其中的一小部分(10%)作为“保留”集。并运用上述公式计算保留集的同现概率矩阵,并累加其中的所有概率值得到一个总概率: 最后尝试各种可能的λ1和 λ2的组合(注:λ1+λ2=1),并且找到总概率最大的那一组λ1和λ2: 很显然λ1=1, λ2=0的组合使得总概率最大。因此,此例中的最佳λ组合的值为:λ1=1,λ2=0 我希望这能为您提供语言模型的正确介绍,代码可以帮助您学习。 二、如何实际数据中运用语言模型
数据来源和预处理
Unigram模型的实际应用
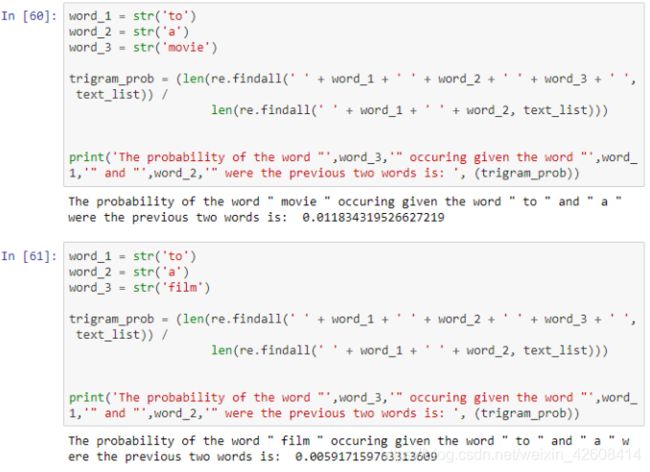
Bigram模型的实际应用
Trigram(3-gram) 模型
三、训练和测试语言模型
Perplexity(复杂度) 定义
信息论中的熵(Entropy)
语言模型中的熵
![]()
四、拟合语言模型的挑战
处理未出现在训练集中的单词:Laplace +1 平滑(Smoothing)
更多的平滑方法
五、如何选择适用的语言模型
退避法(Back-off Method)
插值法
基于IMDB数据集的例子