【滤波专题-第7篇】“类EMD”算法分解后要怎样使用（3）——EMD降噪方法及MATLAB代码实现

使用EMD分解（以及其他“类EMD”分解方法，以下为了简便统称EMD）做信号降噪，是EMD的一个比较重要的应用方向。EMD可以将复杂的信号分解为一系列的固有模态函数（IMFs），每一个IMF都包含了信号的一部分频率信息。在信号降噪的过程中，如何选择和筛选IMFs是关键步骤之一。在本文中，我将介绍EMD降噪的基本步骤以及几种常见的IMFs筛选策略。

一、EMD降噪的通用步骤

EMD降噪的过程可以分为三个基本步骤：EMD分解，IMFs筛选和信号重构。

1. EMD分解：在这一步中，我们使用EMD或者类EMD的方法将复杂的信号分解为一系列的固有模态函数（IMFs）。每一个IMF都包含了信号的一部分频率信息。这就像是将一束光通过棱镜分解为各种颜色一样，每种颜色都代表了一种频率。
2. IMFs筛选：在这一步中，我们根据某种策略来筛选IMFs。这个策略可以基于频率、相关系数、峭度等。筛选的目的是要去掉那些包含噪声的IMFs，而保留那些包含有用信息的IMFs。这就像是从各种颜色中选择我们想要的颜色，而过滤掉我们不想要的颜色。
3. 信号重构：在这一步中，我们将筛选后的IMFs进行叠加，得到降噪后的信号。这就像是将选择的颜色混合在一起，得到我们想要的图像。

二、IMFs筛选策略

下边我将详细介绍几种IMFs筛选的策略：

2.1 根据频谱的直接筛选方法

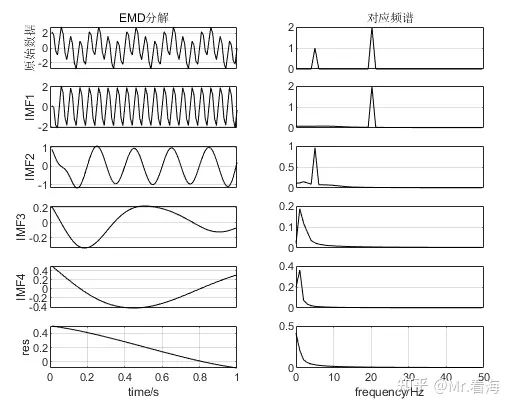
就像之前文章讲到的，EMD方法能将信号分解成若干阶内涵模态分量（IMF分解），并按照频率从高到低进行排列，就像下图（类EMD画图代码可以在这里找到）：

所以我们只要参照各个IMF分量的频谱，选取希望保留的频段重构就可以实现滤波，比如上图中，对IMF1和IMF2两个分量进行重构就基本可以实现5Hz和20Hz的主成分的提取和噪声滤除了。（IMF分量重构方法可以参考这里：“类EMD”算法分解后要怎样使用（2）——高频、低频、趋势项分量判别与重构，及MATLAB代码实现）

上述这种滤波方法需要研究者清晰地知道自己所需的信号频段，不过很多时候我们自己也不知道有用信号的频率范围，这样就需要使用一些辅助手段，比如用某些参数对各分量进行评价，通过设置阈值或者人为判断的方式进行筛选。

2.2 根据相关系数的筛选方法

相关系数是一种衡量两个信号相似性的方法，其值在-1到1之间。相关系数的绝对值越大，两个信号的相似性越高。如果相关系数为正，那么两个信号在相同的方向变化；如果相关系数为负，那么两个信号在相反的方向变化。具体可以看下这里：衡量数据“像不像”——协方差与相关系数 - 知乎 (zhihu.com)

当你使用相关系数来选择IMF时，你可以选择与原始信号高度相关的IMF，因为它们往往包含了信号的主要信息。

选择相关系数阈值的方法是一个权衡过程。阈值过高可能会导致滤除过多的信号信息；阈值过低可能会导致滤除的噪声不足。因此，我们需要根据我们的具体应用和数据的特性，适当地选择阈值。有论文认为，阈值设置为0.5较为合适。[1]

然而，需要注意的是，虽然相关系数是一种有用的工具，但它也有一些限制。例如，它只能衡量两个信号的线性相关性，不能衡量它们的非线性相关性。此外，如果你的信号含有噪声，那么相关系数可能会被噪声影响。

2.3 根据峭度的筛选方法

峭度是一种衡量信号极值分布的指标。一般来说，如果一个IMF的峭度值较大，那么这个IMF可能包含了较多的尖峰或者重尾分布，这些通常与噪声有关。因此，我们可以计算每个IMF的峭度，并据此进行筛选。

具体来说，我们可以设定一个峭度阈值，然后筛选出峭度低于阈值的IMFs。这样，我们就可以将那些可能含有噪声的IMFs去除，从而实现降噪。

正态分布的峭度等于3，峭度小于3时分布的曲线会较“平”，大于3时分布的曲线较“陡”。图片来源：https://www.cnblogs.com/yanshw/p/15963449.html

2.4 一种自适应降噪方法

在论文《基于EEMD的振动信号自适应降噪方法》[2]中，提出了根据白噪声经经验模式分解后其固有模式函数分量的能量密度与其平均周期的乘积为一常量这一特点，设计了自动选择IMF分量重构信号的算法。

具体的步骤可以概括如下：

1. 执行EEMD分解：对含噪声的信号进行EEMD分解，得到K个IMF分量。当然，此处也可以根据需要换成其他分解算法。
2. 计算每个IMF的能量密度与平均周期之积：首先，需要计算每个IMF的能量密度和平均周期。然后，将能量密度与平均周期相乘，得到每个IMF的能量密度与平均周期之积。
3. 计算系数RPi：计算每个IMF的系数RPi，当RPi的值大于等于1时，说明当前IMF的能量密度与平均周期之积相对于前一个IMF的这个值有显著的增加。
4. 筛选IMF分量：当RPi的值大于等于1时，我们认为前面的IMF分量主要包含噪声，因此将其去除。然后，使用剩下的IMF分量重构信号，以实现对原始噪声信号的降噪。

该方法不需要像前几种方法那样还要人为设置阈值，使用起来相对方便一些，但是同时灵活性就相对较低一些了。

2.5 上述方法各自的特点

下表中是上述4个方法的一些主要特点。在使用这些方法时，研究者需要考虑其优势和局限性，以确定是否适合研究的需求。

方法	特点
根据频谱的直接筛选方法	直观而简单：这种筛选方法直接依赖于信号的频谱信息（比如信号的频率分布和频率强度），对于频段的筛选一目了然。 需要频率信息：对于这种筛选方法，研究者需要清楚地知道他们所需要的信号频段。如果研究者不确定有用信号的频率范围，这种方法可能就不适用。 灵活性高：这种筛选方法允许研究者根据他们的需求选择任何特定的频段。
根据相关系数的筛选方法	关注相似性：通过比较IMFs与原始信号的相关系数，识别出包含主要信息的IMFs。 需要设置阈值：在使用相关系数进行筛选时，我们需要设置一个阈值，只有当IMF与原始信号的相关系数超过这个阈值时，我们才认为该IMF包含有用的信息。 只能衡量线性相关性：相关系数只能衡量两个信号的线性相关性，不能衡量他们的非线性相关性。如果信号的相关性是非线性的，那么使用相关系数可能会导致一些信息的丢失。
根据峭度的筛选方法	关注峭度：较大的峭度值通常表示信号有更多的尖峰或重尾分布，这些通常与噪声有关。通过计算每个IMF的峭度，我们可以识别出可能包含噪声的IMFs。 需要设置阈值：在使用峭度进行筛选时，我们需要设置一个峭度阈值，只有当IMF的峭度低于这个阈值时，我们才认为该IMF包含有用的信息。 对高频噪声敏感：峭度在某种程度上对高频噪声较为敏感，因此这种筛选方法在处理含有高频噪声的信号时可能更为有效。
一种自适应降噪方法	自动化筛选：与需要人为设定阈值的筛选方法相比，自适应降噪方法可以自动地选择IMFs分量，这减少了人为干预的需求，使得处理过程更加便捷。 灵活性较低：虽然自适应降噪方法可以自动地进行IMFs筛选，但是它的灵活性较低，可能会得到不理想的效果并无法介入干预。

三、MATLAB案例实现

上边讲到了四种筛选方法，我们现在逐一使用MATLAB进行实现，并初步对比一下滤波效果。

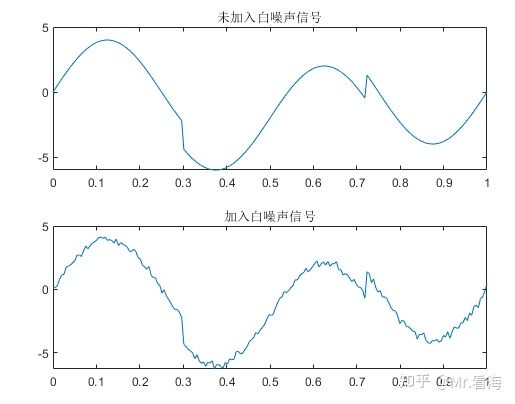
首先我们仿真生成一段信号，并向其中加入白噪声。x为未加入白噪声的纯净信号，sig为加入白噪声后的信号，代码如下：

%% 1.生成仿真信号，x为无噪声信号，sig为添加噪声后的信号
rng(123); %设置随机种子，保证每次生成噪声的一致性
N = 200;
t = linspace(0,1,N);
x = 4*sin(4*pi*t);
x = x - sign(t-0.3) - sign(0.72-t);
sig = x + 0.2*randn(size(t));
figure('Color','w');subplot(2,1,1);plot(t,x);title('未加入白噪声信号')
subplot(2,1,2);plot(t,sig);title('加入白噪声信号')

3.1 基于频谱分析的筛选方法

按照上边讲到的方法，我们首先对信号进行EMD分解，得到一系列IMF分量及其频谱。在之前的文章中，我们提供了快速绘制该图像的函数。此时只需要下边这行代码，就可以画出想要的图像。

%% 2. 对信号进行EMD分解
imfs = pEMDandFFT(sig,1);

此时绘制的图像如下。

然后，我们对每个IMF分量进行频谱分析，经初步分析认为IMF1主要包含噪声信号，所以对IMF2-IMF5以及res进行重构，即将这些IMF分量叠加，得到滤波后的信号。以下是在MATLAB中实现这种方法的代码：

%% 3. 根据频率的直接筛选方法
indices = [2, 3, 4 , 5 , 6];  % 假设我们想要保留的是前两个IMF，需要注意res等同于最后一个IMF，在此例子中，res即IMF5，如果要保留第1、2个IMF和res，可以写成：indices = [1, 2 ,5];
filtered_imfs = imfs(indices, :);
filtered_signal1 = sum(filtered_imfs, 1);

这样就可以得到滤波后的数据filtered_signal1。

我们来画图看一下滤波效果：

%% 4.画滤波前后对比图
% 需要注意，只有在知道纯净信号（即未添加噪声信号）时才能进行指标评价
% 对于真实采样信号，无法获取其纯净信号值的，无法进行该步骤，需删除本小节代码
ori = x;  %无噪声信号
fil = filtered_signal1;  %滤波后信号
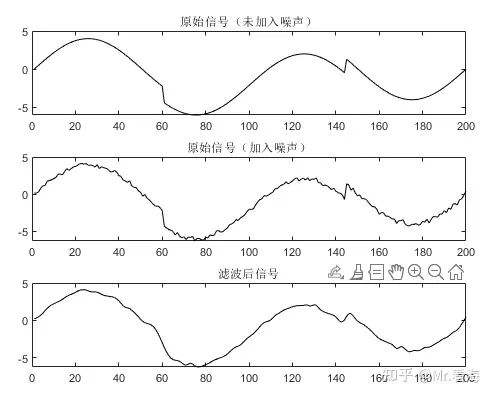
figure('color','w')
subplot(311);plot(x,'k');title('原始信号（未加入噪声）')
subplot(312);plot(sig,'k');title('原始信号（加入噪声）')
subplot(313);plot(fil,'k');title('滤波后信号')
% 注意，对于不知道纯净信号的情况，无法绘制“未加入噪声”的信号图像
% 此时需要将上述4行代码删除，并使用下述3行代码：
% figure('color','w')
% subplot(211);plot(sig,'k');title('原始信号')
% subplot(212);plot(s,'k');title('滤波后信号')

基于频谱分析的筛选方法

结合我们之前讲过的计算一下滤波效果评价指标。计算SNR、MSE和NCC这三个指标值，计算方法也同样进行了封装，就像这样调用就行：

%% 4.进行滤波指标评价
% 需要注意，只有在知道纯净信号（即未添加噪声信号）时才能进行指标评价
% 对于真实采样信号，无法获取其纯净信号值的，无法进行该步骤，需删除本小节代码
[SNR,MSE,NCC] = FilterEffectEvaluation(ori,fil);
% 对滤波效果进行评估
% 目前包含的评估指标有：信噪比SNR，均方差MSE，波形相似系数NCC
% 输入：
% ori：无噪声的原始数据，一维序列
% fil：滤波后的数据，一维序列
disp(['滤波后的SNR、MSE和NCC值分别为：',num2str(SNR),'、',num2str(MSE),'、',num2str(NCC)]);

计算得出滤波后的SNR、MSE和NCC值分别为：25.2919、0.028059、0.99852

这个效果还是可以的，下面我们再计算一下另外几种滤波方法的结果。

3.2 基于相关系数的筛选方法

分析的数据保持不变，使用下述代码可以实现滤波：

%% 3.调用filCorrelation实现滤波
threshold_corr = 0.4;  % 设置相关系数阈值
[filtered_signal2,correlation_values] = filCorrelation(sig, imfs, threshold_corr);
% filCorrelation 基于相关系数进行IMF筛选，用以滤波
%
% 输入:
% original_signal - 原始信号，一维行向量
% imfs - EMD分解得到的IMF分量，每一行对应一个IMF分量
% threshold_corr - 相关系数阈值，用于筛选IMF分量
%
% 输出:
% filtered_signal - 滤波后的信号，一维行向量
% correlation_values - 每个IMF分量的相关系数值，一维行向量

其中的filCorrelation为笔者封装的函数，对于该函数只需要输入待滤波信号sig，模态分解后的分量imf以及相关系数阈值threshold_corr即可，运行程序可以计算出每个分量与sig的相关系数，上边的案例中我将阈值设置成了0.4，此时筛选出的IMF分量为IMF3和IMF4。运行结果如下：

程序执行完之后在MATLAB工作区打印的结果

基于相关系数的筛选方法

选择相关系数阈值是一个平衡的过程，需要根据具体的应用和数据特性来选择。如果阈值设置得过高，可能会滤掉太多的有效信号信息；而阈值设置得过低，则可能无法充分滤除噪声。有研究建议，设置0.5作为一个初始的相关系数阈值，但最终的决定应根据具体情况来调整。

3.3 基于峭度的筛选方法

基于峭度的筛选方法使用下述代码可以实现滤波：

%% 3.调用filKurtosis实现滤波
threshold_kurtosis = 4;  % 设置峭度阈值
[filtered_signal3, kurtosis_values] = filKurtosis(imfs, threshold_kurtosis);
% filKurtosis 基于峭度进行IMF筛选，用以滤波
%
% 输入:
% imfs - EMD分解得到的IMF分量，每一行对应一个IMF分量
% threshold_kurtosis - 峭度阈值，用于筛选IMF分量
%
% 输出:
% filtered_signal - 滤波后的信号，一维行向量
% kurtosis_values - 每个IMF分量的峭度值，一维行向量

其中的filKurtosis为笔者封装的函数，对于该函数只需要输入模态分解后的分量imf以及峭度阈值threshold_kurtosis即可，运行程序可以计算出每个分量的峭度值，上边的案例中我将阈值设置成了4，此时筛选出的IMF分量为IMF3-IMF5以及res。运行结果如下：

程序执行完之后在MATLAB工作区打印的结果

基于峭度的筛选方法

选择峭度阈值时，通常需要参考你的数据特性和具体应用。峭度值较大的IMF一般对应的是含有尖峰或者重尾分布的信号，这样的信号通常与噪声有关。因此，我们通常希望筛选掉这些高峭度的IMF，从而实现对信号的降噪。具体阈值的设定需要对数据进行多次试验观察。可以先设定一个初始值，然后逐步微调，观察滤波效果的变化。通常可以从峭度值的平均值或者中位数作为参考起点。

需要注意的是，峭度阈值的选择需要综合考虑信号的特性和噪声的特性。例如，如果噪声的峭度特别高，可能需要设定较高的阈值才能有效地去除噪声。同时，如果你的信号本身的峭度就较高，那么过低的阈值可能会把有用的信号误删。

3.4 基于自适应降噪方法

上边三种方法都涉及到某些参数的调试，有些同学可能不知道该怎么入手，此时就可以使用基于自适应降噪方法了，基于自适应降噪方法可以使用下述代码可以实现滤波：

%% 3.调用filAdaptive实现滤波
[filtered_signal4, RPi_values] = filAdaptive(imfs);
% filAdaptive 自适应降噪方法
% 参考论文：陈仁祥,汤宝平,马婧华.基于EEMD的振动信号自适应降噪方法[J].振动与冲击,2012,31(15):82-86.DOI:10.13465/j.cnki.jvs.2012.15.015.
%
% 输入:
% imfs - EMD分解得到的IMF分量，每一行对应一个IMF分量
%
% 输出:
% filtered_signal - 滤波后的信号，一维行向量
% RPi_values - 每个IMF分量的RPi值，一维行向量

其中的filAdaptive为笔者封装的函数，对于该函数只需要输入模态分解后的分量imf就行，运行程序可以计算出每个分量的PRi值（具体参数含义详见参考论文），此时筛选出的IMF分量为IMF3-IMF5以及res。运行结果如下：

程序执行完之后在MATLAB工作区打印的结果

基于自适应降噪的筛选方法

这个运行结果和峭度方法相同，不过这是对于本例子的巧合，不是所有信号都会这样哦。

这里有两点注意事项提醒大家：

第一。上边代码中涉及到的封装函数的入口参数imfs，在本例子中是使用的emd分解得到的分量，这里是可以替换成其他的“类EMD”分解方法，比如EEMD、VMD等等，关于这些分解方法在本专栏中都有专篇论述，这里有文章目录：Mr.看海：目录——信号处理有关的那些东东

第二。SNR、NCC和MSE指标，都是需要知道“纯净信号”才能计算的，对于只知道真实含噪信号，不知道纯净信号的情况，是没办法计算这三个指标的。我在之前的文章里进行过详细的说明：Mr.看海：【滤波专题-第4篇】滤波器滤波效果的评价指标（信噪比SNR、均方误差MSE、波形相似参数NCC）

四、关于获取上述MATLAB代码

上述的代码提到了三个新封装的滤波函数，分别用于实现基于相关系数筛选、基于峭度筛选、自适应筛选的IMF分量筛选，从而实现滤波。同学们差不多只需要导入自己要分析的数据，然后直接调用函数就可以了，更多的时间精力可以放在写论文和改进算法上。

我将上述提到的所有代码和案例文件都进行了打包，需要的同学可以下边链接获取：

类EMD滤波算法（相关系数、峭度、自适应等方法） | 工具箱文档

【EMD专题】相关文章：

2.1 Mr.看海：这篇文章能让你明白经验模态分解（EMD）——基础理论篇

2.2 Mr.看海：这篇文章能让你明白经验模态分解（EMD）——IMF的物理含义

2.3 Mr.看海：这篇文章能让你明白经验模态分解（EMD）——EMD在MATLAB中的实现方法

2.4 Mr.看海：希尔伯特-黄变换（HHT）的前世今生——一个从瞬时频率讲起的故事

2.5 Mr.看海：希尔伯特谱、边际谱、包络谱、瞬时频率/幅值/相位——Hilbert分析衍生方法及MATLAB实现

2.6 Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第一篇）——EEMD

2.7 Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第二篇）——CEEMD

2.8 Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第三篇）——CEEMDAN

2.9 Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第四篇）——VMD

2.10 Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第五篇）——ICEEMDAN

2.11 Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第六篇）——LMD

2.12 Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第七篇）——EWT

2.13 Mr.看海：“类EMD”算法分解后要怎样使用（1）——内涵模态分量IMF的方差贡献率、平均周期、相关系数的计算及MATLAB代码实现

2.14 Mr.看海：“类EMD”算法分解后要怎样使用（2）——高频、低频、趋势项分量判别与重构，及MATLAB代码实现

【滤波降噪专题】相关文章：

4.1 Mr.看海：【滤波专题-第1篇】数字滤波器15分钟入门！——这可能是最简单的FIR有限冲激响应滤波讲解

4.2 Mr.看海：【滤波专题-第2篇】数字滤波器15分钟入门！——这可能是最简单的IIR无限冲激响应滤波讲解

4.3 Mr.看海：【滤波专题-第3篇】IIR无限冲激响应和FIR有限冲激响应数字滤波器有什么区别？

4.4 Mr.看海：【滤波专题-第4篇】滤波器滤波效果的评价指标（信噪比SNR、均方误差MSE、波形相似参数NCC）

4.5 Mr.看海：【滤波专题-第5篇】FIR、IIR滤波器设计及MATLAB实现

4.6 Mr.看海：【滤波专题-第6篇】小波阈值去噪方法看这一篇就明白了~（附MATLAB实现）

参考

1. ^[1]陈仁祥,汤宝平,吕中亮.基于相关系数的EEMD转子振动信号降噪方法[J].振动.测试与诊断,2012,32(04):542-546+685.DOI:10.16450/j.cnki.issn.1004-6801.2012.04.005.
2. ^[1]陈仁祥,汤宝平,马婧华.基于EEMD的振动信号自适应降噪方法[J].振动与冲击,2012,31(15):82-86.DOI:10.13465/j.cnki.jvs.2012.15.015.