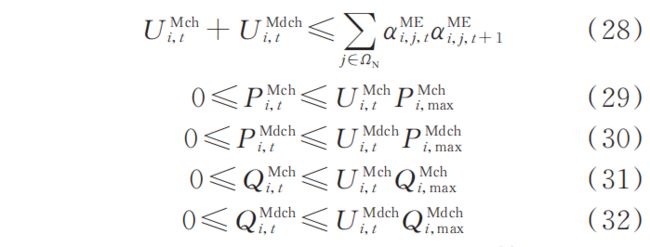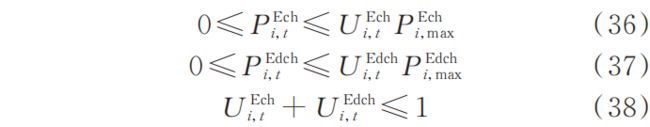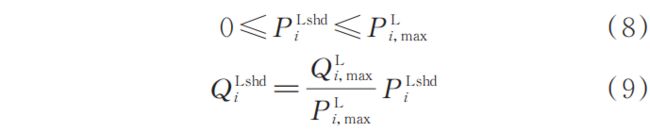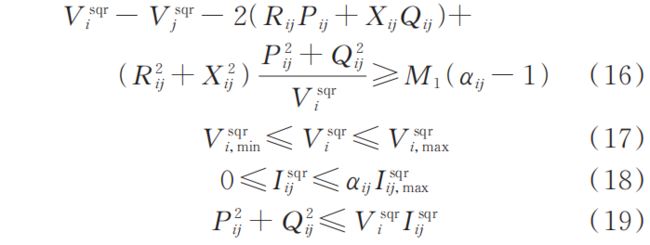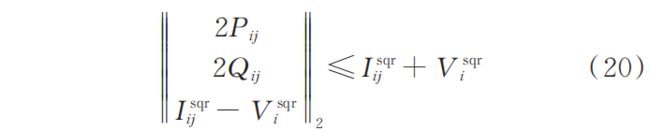(文章复现)面向配电网韧性提升的移动储能预布局与动态调度策略(2)-灾后调度matlab代码

参考文献：

[1]王月汉,刘文霞,姚齐,万海洋,何剑,熊雪君.面向配电网韧性提升的移动储能预布局与动态调度策略[J].电力系统自动化,2022,46(15):37-45.

1.基本原理

1. 1 目标函数

        在灾害发生后，配电网失去主网供电，设故障的持续时间可根据灾害强度和抢修资源数量做出预测。以故障持续时间内负荷削减功率加权值最小为目标，建立多源协同的灾后恢复优化模型，通过动态调度移动储能、电动汽车与柴油发电机，最大限度提升配电网韧性，目标函数如下：

1. 2 约束条件

1. 2. 1 移动储能的时空动态调度约束

        在电网-交通网融合系统中，移动储能的调度状态由其充放电状态和交通运输状态共同决定，具有时空耦合特性。考虑移动储能i在节点j与节点 k 间的交通通行时间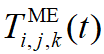与安装配置时间，建立移动储能的时空动态调度模型，设运输过程不消耗电能，其时空动态调度如图2所示。

        由于交通网络容易受到实时路况、突发事件影响，在不同灾害时段与路况影响下移动储能在相同道路的实际通行时间可能存在差异[21]。为了保证灾害场景下应急移动储能设备通行的可靠性，本文考虑冰雪等全覆盖型灾害对交通状况的影响，通过交通融合系数来反映移动储能的实际车速与等效通行距离之间的空间调度关系[17] 。

1. 2. 2 电动汽车充放电约束

        假设电动汽车充电桩与电动汽车均满足“车网互动”条件，即可向电网输电。在灾害发生后，接入充电桩的电动汽车可通过电池放电向负荷提供电能，其充放电功率和荷电状态需要满足以下约束：

1. 2. 3 其他约束

        在灾后恢复阶段,各时刻的负荷削减功率、分布式电源出力与配电网运行仍需要满足相应约束,约束条件形式与灾前预布局阶段相同﹐见式(8)—式(20)。

2 模型求解

        灾后恢复优化模型为混合整数二阶锥规划问题，可利用商业求解器 Gurobi 求解。

3.编程思路分析

3.1参数和变量定义

表1 相关参数

 表2 决策变量

 

3.2编程思路

        根据对文献内容的解读，可以设计下面的编程思路：

步骤1：输入所需数据

        部分数据和灾前移动储能预配置阶段的相同，继续用就行其他的数据可在原文提供的附录中获取，这部分主要的问题和难点如下：

        获取各节点的距离矩阵。原文中给出的假设是交通网拓扑与电网相同，相邻电气节点间的道路距离为 2 km。但是，在文章的背景中，由于考虑了配电网重构，配电网拓扑结构可能会不断变化，交通网不可能随着电网拓扑变化。所以假设交通网和初始配电网拓扑相同。另外，需要用到的距离矩阵是所有节点两两之间的距离，目前已知的是相邻节点的距离，需要采用图论算法进行求解。

        步骤2：定义决策变量

        这一步比较简单，按照表2，初始化决策变量即可。要注意的是每个决策变量的维度以及类型(sdpvar还是binvar)不要出错。

        需要注意一点，由于文中共有两个移动储能车，33个节点，11个时段，如果采用常规变量定义方式，alpha_ME将是一个2×33×11的三维变量，这么处理会大大降低程序运行速率。为了方便起见，将定义两个33×11的二维变量，alpha_ME1和alpha_ME2，就可以避免使用三维决策变量。

        步骤3：定义目标函数和约束条件，尝试求解确定性优化问题

        按照原文中给定的公式，写出相应的目标函数与约束条件即可。但文中涉及的优化问题是一个多时段的混合整数二阶锥优化，如果采用常规的思维，在写约束条件时经常会用到三层以上的循环，大大拖慢程序运行速度，可以采用一些小技巧避免多层循环的使用，提高程序效率。

        1.以约束条件(26)为例说明如何避免多重循环的使用。式(26)只写了t的取值范围，如果把其他下标的取值范围都标上，式(26)就变成了下面这样：

        按常规思维来看，需要写成5层循环的形式，matlab代码如下：

for t = 1:NT
    for i = 1:NME
        for j = 1:NB
            for k = 1:NB
                for dt = 1:min([floor(T_ME(j,k,t)),NT-t])
                    Constraints = [Constraints , alpha_ME(i,j,t) + alpha_ME(i,k,t+dt) <= 1];
                end
            end
        end
    end
end

        首先，在定义决策变量时，就已经把两个移动储能的决策变量分开表示，可以减小一层循环，另外，可以将j,k两层循环写成一组数对，方法如下：

j_index = zeros(1,33*33);
k_index = zeros(1,33*33);
it = 1;
for j = 1:33
    for k = 1:33
        j_index(it) = j;
        k_index(it) = k;
        it = it + 1;
    end
end

        其中j_index和k_index都是1089(33×33)维的数据，把这两个变量提前存在工作区，使用时读取出来，就可以把5层循环减小到2层循环，如下所示：

for t = 1:NT
    for dt = 1:min([floor(T_ME(j_index(k),k_index(k),t)),NT-t])
        % 式26
        Constraints = [Constraints , alpha_ME1(j_index,t) + alpha_ME1(k_index,t+dt) <= 1 , alpha_ME2(j_index,t) + alpha_ME2(k_index,t+dt) <= 1];
    end
end

        经过这样处理，运行时间从原本的0.383611秒减小到0.001126秒，提升的效率达到了99.71%。我只是以约束条件(26)为例进行说明，当优化问题非常复杂时，减少循环语句的使用对程序运行效率的提升是非常惊人的。

        2.另外再强调一点，配电网最优潮流最容易踩坑的地方就是标幺值转换上。之前有朋友拿自己写的代码问我，说感觉公式模型都是按照参考文献打的，但一用求解器就是“Infeasible problem”，拿给我一看，参数中有的数值用的是实际值，有的数值用的是标幺值，非常混乱，我把参数统一修改为标幺值就可以正常运行了。建议在编程时都转换为标幺值求解。

        这一步是最难的部分，需要有耐心，反复调试。为了避免在大段约束条件中寻找错误，建议是每加上一条约束条件，便调试一下模型是否可解，如果可解，再加入下一个约束条件，否则需要反复调试，找到问题所在。

        步骤4：输出计算结果

        原文中将移动储能的预布局和优化调度拆成两阶段优化策略，第二阶段为多源协同的灾后恢复优化模型，是一个混合整数二阶锥规划模型(MISOCP)。这份代码复现了第二阶段多源协同的灾后恢复优化模型的结果，第一阶段的结果可以查看我之前的博客。

4.完整Matlab代码

        完整的matlab代码可以从这个链接获取：

两阶段鲁棒韧性提升策略

5.运行结果分析

5.1表2 移动储能的动态调度结果

 

5.2 图B3 灾害发生后光伏机组的预测出力 

5.3 图4 各时段负荷功率和恢复比例 

5.4 图B4 移动储能有功功率输出与接入位置的关系

5.5 图B5 移动储能荷电状态与接入位置的关系 

5.6 图B6 灾后恢复阶段柴油发电机有功功率输出