数据结构初阶(3)(链表:链表的基本概念、链表的类型、单向不带头非循环链表的实现、链表的相关OJ练习、链表的优缺点 )
接上次博客:和数组处理有关的一些OJ题;ArrayList 实现简单的洗牌算法(JAVA)(ArrayList)_di-Dora的博客-CSDN博客
目录
链表的基本概念
链表的类型
单向、不带头、非循环链表的实现
遍历链表并打印节点值:
在链表头部插入节点:
在链表尾部插入节点:
得到单链表的长度 :
查找是否包含关键字key是否在单链表当中:
删除第一次出现关键字为key的节点 (两种实现方式):
删除所有值为key的节点:
指定任意位置插入数据:
清空链表:
OJ练习
链表的优缺点
数组是一块连续的内存,逻辑上和物理内存上都是连续的;
链表是在逻辑上是连续的,但是在物理内存上是不连续的。
链表的基本概念
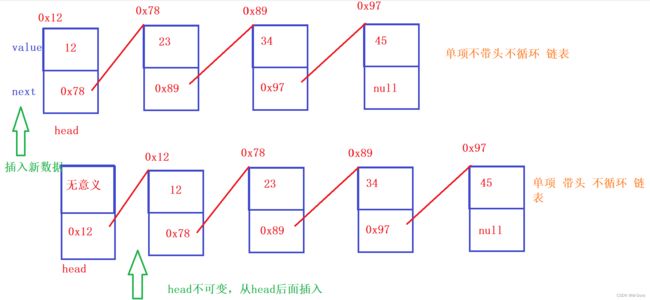
链表是一种常见的数据结构,它由一系列节点组成,每个节点包含两部分:数据元素 (value) 和指向下一个节点的指针 ( next 域 )。通过这些节点的连接,可以形成一个链式结构。
链表的基本概念如下:
1、节点(Node):链表的基本单元,包含数据元素和指针。数据元素可以是任意类型的数据,指针指向下一个节点。每个节点都是一个对象。最后一个节点的 next 域是 null 。
2、头节点(Head):链表的第一个节点,用于标识链表的起始位置。通常使用一个指针变量来指向头节点。
3、尾节点(Tail):链表的最后一个节点,其指针指向空(NULL),表示链表的结束。
4、链表长度(Length):链表中节点的数量,可以通过遍历链表来计算。
5、空链表(Empty List):不包含任何节点的链表。
6、单向链表(Singly Linked List):每个节点只有一个指针,指向下一个节点。最后一个节点的指针指向空。
7、双向链表(Doubly Linked List):每个节点有两个指针,一个指向前一个节点,一个指向下一个节点。头节点的前一个指针和尾节点的后一个指针都指向空。
注意:
1.链式结构在逻辑上是连续的,但是在物理上不一定连续;
2.现实中的节点一般都是从堆上申请出来的;
3.从堆上申请的空间,是按照一定的策略来分配的,两次申请的空间可能连续,也可能不连续。
链表的类型
链表的组合方式有多种,可以根据以下两个方面来区分和计算组合的种类:
1、单向链表和双向链表:
根据节点的指针数量,链表可以分为单向链表和双向链表。
单向链表每个节点只有一个指针,指向下一个节点;
而双向链表每个节点有两个指针,分别指向前一个节点和后一个节点。
2、是否带头节点:
带头节点的链表在第一个节点之前有一个额外的头节点,用于标识链表的起始位置。(head的value是无意义的,如果想从最开头插入数据时,head是不可变的,从head后面插入)
而不带头节点的链表则直接以第一个节点作为链表的起始位置。(head是有value的,如果想从最开头插入数据时,head是可变的,变成新插入的数据)
3、是否循环:
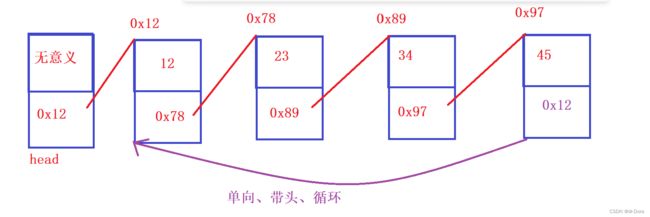
循环链表是在链表的尾部节点和头部节点之间形成一个循环连接,使得链表的最后一个节点指向头部节点。
综合考虑上述两个方面,我们可以得到链表的组合方式共有8种:
单向、不带头节点、非循环链表(重点)
单向、不带头节点、循环链表
单向、带头节点、非循环链表
单向、带头节点、循环链表
双向、不带头节点、非循环链表(重点)
双向、不带头节点、循环链表
双向、带头节点、非循环链表
双向、带头节点、循环链表
每种组合方式都有自己的特点和应用场景,我们可以根据具体需求选择合适的链表类型。
单向、不带头、非循环链表的实现
我们可以先来实现一个最简易的链表,即手动创建一个单向链表:
public class MySingleList {
static class ListNode {
public int val; // 节点的值域
public ListNode next; // 下一个节点的地址
public ListNode(int val) {
this.val = val;
}
}
public ListNode head; // 表示当前链表的头节点
//我们先来写一个最笨的方法:手动创建链表节点
public void createlist() {
// 创建链表节点
head = new MySingleList.ListNode(-1);
MySingleList.ListNode node1 = new MySingleList.ListNode(12);
MySingleList.ListNode node2 = new MySingleList.ListNode(23);
MySingleList.ListNode node3 = new MySingleList.ListNode(34);
MySingleList.ListNode node4 = new MySingleList.ListNode(45);
MySingleList.ListNode node5 = new MySingleList.ListNode(56);
// 构建链表关系
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
this.head = node1;//head 是一个指向第一个节点的引用
}
}public class Test {
public static void main(String[] args) {
MySingleList list = new MySingleList();
list.createlist();
System.out.println(list);
System.out.println("12345");
}
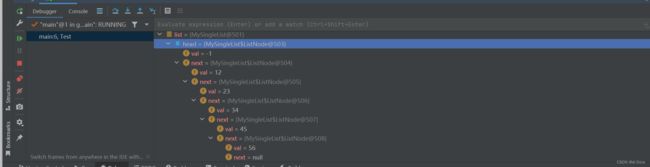
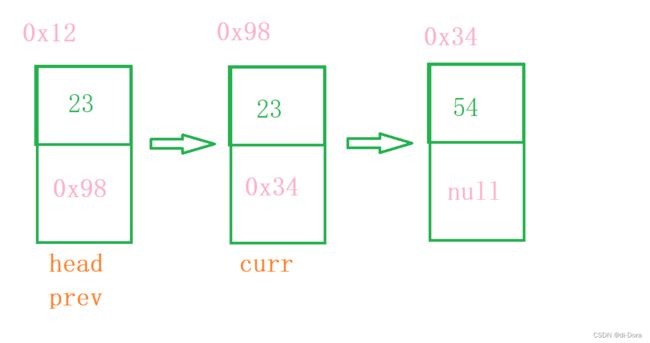
}通过这个代码,我们可以直观地观察到链表的大致结构:
好了,现在我们就正式开始实现一个完整的单向链表了:
首先我们还是先给出链表的基本代码:
我们先要有一个引用 head 指向第一个节点,它是“节点”类型,就如同 Person person = new Person; 一样。
链表的头节点,是链表的成员变量、链表的属性,而不是一个节点类的成员变量。
public class MySingleList {
static class ListNode {
public int val; // 节点的值域
public ListNode next; // 下一个节点的地址
public ListNode(int val) {
this.val = val;
}
}
public ListNode head; // 表示当前链表的头节点
// 在链表头部插入节点
public void insertAtHead(int val)
// 在链表尾部插入节点
public void insertAtTail(int val)
//得到单链表的长度
public int size()
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key)
//删除第一次出现关键字为key的节点
public void deleteNode(int key)
// 删除所有值为key的节点
public void removeAllKey(int key)
//任意位置插入,第一个数据节点为0号下标
public void insertAtIndex(int index, int val)
// 遍历链表并打印节点值
public void display()
// 清空链表
public void clear()
}以上都是我们需要实现的方法。
先来实现第一个:
遍历链表并打印节点值:
// 遍历链表并打印节点值
public void display() {
//不可以让head本身移动,否则将遗失head的位置
ListNode curr = head;
while (curr != null) {
System.out.print(curr.val + " ");
curr = curr.next; //引用向后移动一位
}
System.out.println();
}
这里我们要注意:curr 是一个引用!!!
curr = null 代表的是已经遍历了整个链表。
在链表头部插入节点:
// 在链表头部插入节点
//一般建议,再插入的时候,先绑定后面的节点信息
//就算链表中一个代码都没有,也不影响我们插入节点
//以头插法插入,数据是倒序的
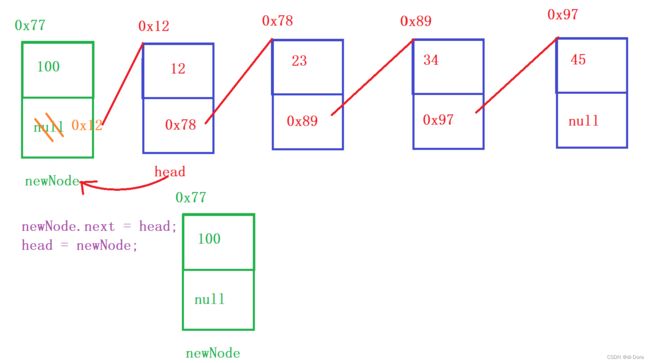
public void insertAtHead(int val) {
ListNode newNode = new ListNode(val);
newNode.next = head;
head = newNode;
} public static void main(String[] args) {
MySingleList list = new MySingleList();
//list.createlist();
list.insertAtHead(12);
list.insertAtHead(23);
list.insertAtHead(34);
list.insertAtHead(45);
list.insertAtHead(56);
list.display();
}注意:以头插法插入,数据是倒序的:
在链表尾部插入节点:
// 在链表尾部插入节点
public void insertAtTail(int val) {
ListNode newNode = new ListNode(val);
//cur = null 代表把链表的每一个节点都遍历完了
//cur.next = null 代表cur现在是最后一个节的位置
//一定要写,否则会报:空指针异常
//如果head等于null,curr也就等于null,就不存在curr.next
if (head == null) {
head = newNode;
} else {
ListNode curr = head;
while (curr.next != null) {
curr = curr.next;
}
curr.next = newNode;
}
}
注意区分:
curr = null 表示当前节点 curr 引用已经指向了链表的末尾,即已经遍历完了链表的所有节点。在这种情况下,可以用来判断是否已经遍历到了链表的末尾。
curr.next = null 表示当前节点 curr 的下一个节点指针指向 null,即当前节点 curr 是链表中的最后一个节点。这通常用于在遍历链表时进行判断,以确定是否已经到达了链表的末尾节点。
得到单链表的长度 :
//得到单链表的长度
public int size() {
int length = 0;
ListNode curr = head;
while (curr != null) {
length++;
curr = curr.next;
}
return length;
}查找是否包含关键字key是否在单链表当中:
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key) {
ListNode curr = head;
while (curr != null) {
if (curr.val == key) {
return true;
}
curr = curr.next;
}
return false;
}删除第一次出现关键字为key的节点 (两种实现方式):
找到你要删除的节点的前驱,用 del = curr.next;进行删除:curr.next = del.next;
//删除第一次出现关键字为key的节点
//找到指定删除的节点的前一个节点,即找到key的前驱
public void deleteNode(int key) {
if (head == null) {
System.out.println("当前链表无数据");
return;
}
//单独删除头节点
if (head.val == key) {
head = head.next;
return;
}
ListNode curr = head;
//如果 curr.next = null ,表示已经没有下一个节点了
while (curr.next != null) {
if (curr.next.val == key) {
curr.next = curr.next.next;
return;
}
//curr 后移,继续往后寻找
curr = curr.next;
}
}
//删除第一次出现关键字为key的节点 -------第2种方法
public void remove(int key){
if(head == null) {
System.out.println("当前链表无数据");
return;
}
//单独删除头节点
if(head.val == key) {
head = head.next;
return;
}
ListNode cur = searchPrev(key);
if(cur == null) {
System.out.println("没有你要删除的数字");
return;
}
ListNode del = cur.next;
cur.next = del.next;
}
private ListNode searchPrev(int key) {
ListNode cur = head;
while (cur.next != null) {
if(cur.next.val == key) {
return cur;
}
cur = cur.next;
}
return null;
}删除所有值为key的节点:
删除所有值为key的节点?那我们遍历链表直到找不到key不就好了?
不可以想得那么简单!我们需要快速的一次性删除!
我们需要定义两个引用:
curr:代表当前需要删除的节点;prev:代表要删除节点的前驱。
如果头节点的 val 就是 key 怎么办?
我们先来看看第一种写法:
public void removeAllKey(int key) {
if(head==null){
return;
}
ListNode prev = head;
ListNode curr = head.next;
while (curr != null) {
if (curr.val == key) {
prev.next = curr.next;
} else {
prev = curr;
}
curr = curr.next;
}
//删除头节点
if(head.val==key){
head=head.next;
}
}可不可以把我们最后的
//删除头节点
if(head.val==key){
head=head.next;
}放到前面呢?
如果将删除头节点的代码放到前面,可能会导致以下问题:
如果我们将删除头节点的代码放到循环的前面,那么在进入循环之前,我们会执行删除头节点的操作。这意味着我们将删除链表的头节点,并将指针 head 指向下一个节点。此时,prev 和 curr 指针都指向了同一个节点,即原链表的第二个节点。
然后,循环开始执行,根据通常的逻辑,我们应该检查当前节点 curr 的值是否等于目标值 key,并相应地删除节点。然而,在这种情况下,由于 prev 和 curr 指向相同的节点,将 prev 和 curr 都指向下一个节点,而不检查该节点的值是否等于 key。
这样就会导致我们跳过了一个节点,下一次循环中的 curr 实际上已经指向了原链表中的第三个节点,而不是第二个节点。因此,我们没有对当前节点进行值的检查,可能会导致跳过了一个需要删除的节点。
这种错误的结果是因为删除头节点的操作被放置在了循环之前,导致循环内的删除操作出现了逻辑错误。正确的做法是在循环中进行节点的删除操作,并根据节点的值进行判断和处理,而不是提前删除头节点。
因此,将删除头节点的代码放到前面会导致以上问题。为了确保算法正确地删除所有的值等于 key 的节点,需要将删除头节点的代码放在循环之后,这样我们可以正确地处理链表中的所有节点。
那还有没有别的方法?
我们来看看第二种写法:
// 删除所有值为key的节点
public void removeAllKey(int key) {
ListNode dummy = new ListNode(0); // 创建一个虚拟头节点,方便处理头节点的情况
dummy.next = head;
ListNode prev = dummy;
ListNode curr = head;
while (curr != null) {
if (curr.val == key) {
prev.next = curr.next;
} else {
prev = curr;
}
//prev不可以移动!可能下一个节点仍为key!
curr = curr.next;
}
head = dummy.next;
}这段代码采用了虚拟头节点的方式来简化对头节点的处理:
首先,代码创建了一个名为 dummy 的虚拟头节点,并将其指向原链表的头节点,即 dummy.next = head。这样做是为了在处理头节点时能够与其他节点一样进行相同的操作。
然后,定义了两个指针 prev 和 curr,初始时 prev 指向虚拟头节点 dummy,curr 指向原链表的头节点 head。
接下来,进入了一个循环,循环条件是 curr 不为 null,即遍历链表直到 curr 为最后一个节点。
在循环内部,首先判断当前节点 curr 的值是否等于目标值 key。如果相等,表示需要删除该节点。此时,将 prev.next 指向 curr.next,即将 prev 的下一个节点指向 curr 的下一个节点,实现了删除当前节点的操作。
如果当前节点的值不等于目标值 key,则将 prev 移动到当前节点 curr 的位置,即 prev = curr。这样做是为了保持 prev 始终指向当前节点的前一个节点,方便在需要删除节点时修改链表的连接关系。
无论当前节点的值是否等于目标值 key,最后都将 curr 指向下一个节点,即 curr = curr.next,继续遍历下一个节点。
循环结束后,原链表中所有值为 key 的节点都已经被删除,此时需要更新头节点的指向。将 head 指向虚拟头节点的下一个节点,即 head = dummy.next,完成了删除操作。
总之,该方法使用虚拟头节点来简化对头节点的处理,通过遍历链表,找到需要删除的节点,并修改节点间的连接关系,最终实现了删除链表中所有值为 key 的节点的功能。
指定任意位置插入数据:
定义一个引用 curr,让它走到即将插入位置的前一个位置,这样我们可以同时访问到插入位置前和插入位置后的节点。先把 curr.next 赋值给newNode.next ,即新插入节点的指向原来位于插入位置的节点,再把 curr.next 变成 newNode 的值。
往 0 位置插入,相当于头插法,往结尾插入,相当于尾插法。
//任意位置插入,第一个数据节点为0号下标
public void insertAtIndex(int index, int val) {
if (index < 0 || index > size()) {
throw new IndexOutOfBoundsException("Invalid index: " + index);
}
if (index == 0) {
insertAtHead(val);
return;
}
if(index==size()){
insertAtTail(val);
return;
}
ListNode newNode = new ListNode(val);
ListNode curr = head;
int count = 0;//定义一个计数器
while (curr != null && count < index - 1) {
curr = curr.next;
count++;
}
if (curr == null) {
throw new IndexOutOfBoundsException("Invalid index: " + index);
}
newNode.next = curr.next;
curr.next = newNode;
}或者,你也可以单独封装出去一个方法:
private ListNode findIndexSubOne(int index){
ListNode curr=head;
while (index-1!=0){
curr=curr.next;
index--;
}
return curr;
}清空链表:
// 清空链表
public void clear() {
head = null;
}最后可以测试了看看:
public class Test {
public static void main(String[] args) {
MySingleList list = new MySingleList();
//list.createlist();
list.insertAtHead(12);
list.insertAtHead(23);
list.insertAtHead(34);
list.insertAtHead(45);
list.insertAtHead(56);
list.display();
list.insertAtTail(666);
list.display();
list.deleteNode(12);
list.display();
list.insertAtTail(23);
list.insertAtTail(34);
list.insertAtTail(45);
list.insertAtTail(23);
list.display();
list.removeAllKey(23);
list.display();
list.insertAtIndex(2,99999);
list.display();
list.insertAtIndex(5,188);
list.display();
int lengh=list.size();
System.out.println(lengh);
}
}现在我们以及了解了链表大致方法的底层逻辑了,为了巩固知识,接下来,我们一起做一些OJ练习吧。
OJ练习
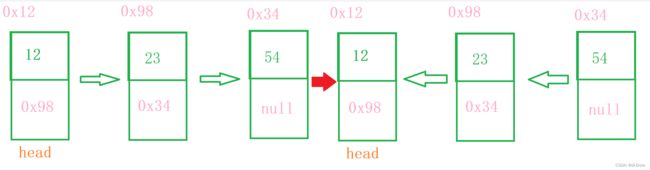
1、给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
这是一个笔试面试里面经常考察的问题,所以蛮重要的。
使用头插法:
(1)、迭代:
class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
class Solution {
public ListNode reverseList1(ListNode head) {
if(head == null) return null;
if(head.next == null) return head;
//cur从第二个节点开始
ListNode cur = head.next;
//先将第一个节点next 置为空,因为它一定是最后一个节点
head.next = null;
while(cur != null) {
//记录下来 当前需要翻转的节点的下一个节点
ListNode curNext = cur.next;
cur.next = head;
head = cur; // 将 cur 设置为新的头节点
cur = curNext;
}
return head;
}
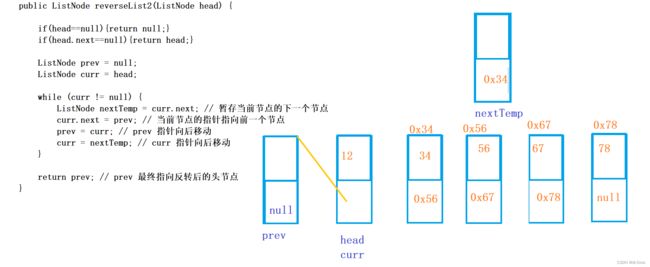
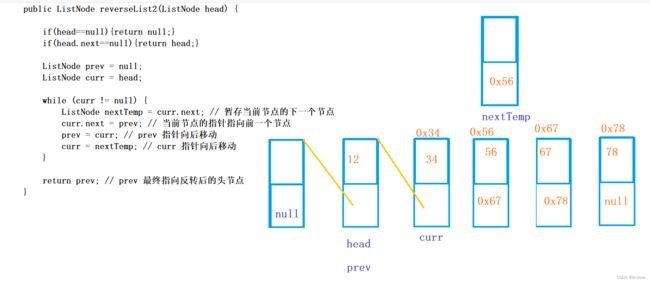
public ListNode reverseList2(ListNode head) {
if(head==null){return null;}
if(head.next==null){return head;}
ListNode prev = null;
ListNode curr = head;
while (curr != null) {
ListNode nextTemp = curr.next; // 暂存当前节点的下一个节点
curr.next = prev; // 当前节点的指针指向前一个节点
prev = curr; // prev 指针向后移动
curr = nextTemp; // curr 指针向后移动
}
return prev; // prev 最终指向反转后的头节点
}
}第一种方法中,使用了两个指针 cur 和 curNext,以及一个变量 head 来记录头节点。在每次迭代中,将当前节点 cur 的 next 指针指向前一个节点 head,然后更新 head 为 cur,最后将 cur 更新为下一个节点 curNext。最终返回 head 作为反转后的链表头节点。
第二种方法中,使用了两个指针 prev 和 curr,分别表示当前节点的前一个节点和当前节点。
- 首先进行特殊情况的处理。如果链表为空或只有一个节点,直接返回链表本身。
- 初始化两个指针 prev 和 curr,分别指向前一个节点和当前节点,初始时 prev 为null,curr 指向链表的头节点。
- 进入循环,循环条件为 curr 不为null。
- 在循环内部,首先暂存当前节点 curr 的下一个节点,将其保存在 nextTemp 中,以防断开链表。
- 将当前节点 curr 的指针指向前一个节点 prev,实现反转操作。
- 更新 prev 指针为当前节点 curr,将其向后移动。
- 更新 curr 指针为暂存的下一个节点 nextTemp,将其向后移动。
- 循环结束后,链表的所有节点都被反转,并且 prev 指向了反转后的头节点。
- 返回 prev,即为反转后的链表的头节点。
大概如下图:相当于创建了一个节点作为最后的尾巴,反正是无意义的:
(2)、递归:
public ListNode reverseList(ListNode head) {
// 递归终止条件:如果链表为空或只有一个节点,则直接返回该节点
if (head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next); // 递归反转后续链表
head.next.next = head; // 将当前节点的下一个节点的指针指向当前节点,实现反转
head.next = null; // 将当前节点的指针指向 null,避免形成环
return newHead; // 返回反转后的头节点
}这两种方法都可以实现链表的反转。迭代方法通过维护两个指针 prev 和 curr 来逐个反转节点的指针指向,直至遍历完整个链表。递归方法则通过递归调用先反转后续链表,再修改当前节点和后续节点的指针指向来实现反转。最后,两种方法都返回反转后的头节点。
2、给你单链表的头结点 head,请你找出并返回链表的中间结点。如果有两个中间结点,则返回第二个中间结点。
要找出链表的中间节点,我们可以使用“快慢指针”的思想:
定义两个指针,一个慢指针 slow 和一个快指针 fast,初始时都指向链表的头节点 head。
快指针 fast 每次移动两步,慢指针 slow 每次移动一步。当快指针到达链表末尾时,慢指针恰好到达链表的中间位置。
public ListNode middleNode(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}在每次迭代中,快指针 fast 先向后移动两步,如果链表长度为奇数,则慢指针 slow 恰好指向中间节点;如果链表长度为偶数,则慢指针 slow 指向中间两个节点的后一个节点。
最终,返回慢指针 slow 所指向的节点作为链表的中间节点。
但是,请注意,上述代码假设链表的头节点不为 null,并且没有循环或环形结构。如果链表可能存在环,请先检查是否有环再应用上述算法。
还有,我们这个地方:
while (fast != null && fast.next != null)不可以写成:
while (fast.next != null && fast != null )因为,当 fast 为 null 时,如果我们先判断 fast.next != null,会出现 NullPointerException。因为当 fast 为 null 时,无法继续访问 fast.next,会抛出异常。
3、输入一个链表,输出该链表中倒数第k个结点。
要输出链表中倒数第k个节点,我们还是可以使用双指针的方法:
要找到链表中倒数第 k 个节点,可以使用双指针法。定义两个指针,一个指针 fast 和一个指针 slow,初始时都指向链表的头节点 head。
首先,将 fast 指针向前移动 k-1 步,使得 fast 指针和 slow 指针之间相隔 k-1 个节点。然后,同时移动 fast 和 slow 指针,直到 fast 指针到达链表的末尾。此时,slow 指针指向的节点就是倒数第 k 个节点。
如果链表的长度小于 k,即链表节点数不足 k 个,则无法找到倒数第 k 个节点,返回 null。
public ListNode FindKthToTail(ListNode head, int k) {
if (head == null || k <= 0) {
return null;
}
ListNode fast = head;
ListNode slow = head;
// 将 fast 指针向前移动 k-1 步
for (int i = 0; i < k - 1; i++) {
if (fast.next != null) {
fast = fast.next;
} else {
// 如果链表长度小于 k,返回 null
return null;
}
}
// 同时移动 fast 和 slow 指针
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}在代码中,首先进行一些边界条件的判断,如果链表为空或者 k 的值小于等于 0,直接返回 null。
然后,使用快指针 fast 先向前移动 k-1 步。在移动过程中需要注意判断是否已经到达链表末尾,如果到达末尾但还没有移动 k-1 步,则链表长度不足 k,返回 null。
接下来,使用快指针 fast 和慢指针 slow 同时移动,直到 fast 指针到达链表末尾。此时,slow 指针指向的节点就是倒数第 k 个节点。
最后,返回 slow 指针指向的节点作为结果。
需要注意的是,在处理边界情况时要进行额外的判断,例如链表长度小于 k 或链表长度等于 k 的情况。
4、将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
这也是一道经典题型!
(1)、迭代法:
- 创建一个新的虚拟头节点 dummy,以及一个指针 curr 指向 dummy。
- 在每次迭代中,比较两个链表的当前节点 list1 和 list2 的值,将较小值的节点接到 curr 的后面,并将对应链表的指针向后移动一位。
- 最终,当其中一个链表到达末尾时,将另一个链表的剩余部分直接接到 curr 的后面。
- 返回 dummy.next,即为合并后的链表头节点。
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode dummy = new ListNode(0); // 创建虚拟头节点
ListNode curr = dummy; // 当前节点指针
while (list1 != null && list2 != null) {
if (list1.val <= list2.val) {
curr.next = list1;
list1 = list1.next;
} else {
curr.next = list2;
list2 = list2.next;
}
curr = curr.next;
}
// 将剩余的链表部分直接接到 curr 的后面
if (list1 != null) {
curr.next = list1;
}
if (list2 != null) {
curr.next = list2;
}
return dummy.next; // 返回合并后的链表头节点
}(2)、递归法:
- 递归地比较两个链表的当前节点 list1 和 list2 的值,选择较小值的节点作为合并后的链表的当前节点,并将其 next 指针指向递归调用的结果。
- 递归终止条件是当其中一个链表为空时,直接返回另一个链表。
- 返回合并后的链表头节点。
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if (list1 == null) {
return list2;
}
if (list2 == null) {
return list1;
}
if (list1.val <= list2.val) {
list1.next = mergeTwoLists(list1.next, list2);
return list1;
} else {
list2.next = mergeTwoLists(list1, list2.next);
return list2;
}
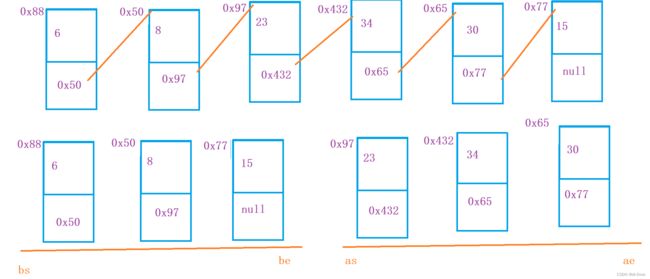
}5、现有一链表的头指针 ListNode* pHead,给一定值x,编写一段代码将所有小于x的结点排在其余结点之前,且不能改变原来的数据顺序,返回重新排列后的链表的头指针。
- 定义四个指针 bs、be、as、ae,分别表示小于 x 的节点链表的头指针、尾指针,以及大于等于 x 的节点链表的头指针、尾指针。
- 初始化当前节点指针 cur 为链表的头指针。
- 进入循环,遍历整个链表。
- 在循环中,根据当前节点的值与 x 的比较结果,将节点插入到对应的节点链表中。
- 如果当前节点的值小于 x,则将其插入小于 x 的节点链表中
public ListNode partition(ListNode pHead, int x) {
// write code here
ListNode bs = null;
ListNode be = null;
ListNode as = null;
ListNode ae = null;
ListNode cur = pHead;
//没有遍历完 整个链表
while(cur != null) {
if(cur.val < x) {
//第一次插入
if(bs == null) {
bs = be = cur;
}else {
be.next = cur;
be = be.next;
}
}else {
//第一次插入
if(as == null) {
as = ae = cur;
}else {
ae.next = cur;
ae = ae.next;
}
}
cur = cur.next;
}
//第一个段 没有数据
if(bs == null) {
return as;
}
be.next = as;
//防止 最大的数据 不是最后一个
//注意看我们的图片,如果不改的话,形成环
if(as!=null) {
ae.next = null;
}
return bs;
}或者使用两个指针来实现(其实两个方法是几乎一毛一样的):
(1)、创建两个新的链表,smallerHead 和 greaterHead,分别代表小于 x 的节点和大于等于 x 的节点的链表。同时创建两个尾节点指针 smallerTail 和 greaterTail,初始时它们都指向对应链表的头节点。
(2)、遍历原始链表 pHead:
- 如果当前节点的值小于 x,将其插入到 smallerTail 的后面,并将 smallerTail 指向新插入的节点,更新 smallerTail。
- 如果当前节点的值大于等于 x,将其插入到 greaterTail 的后面,并将 greaterTail 指向新插入的节点,更新 greaterTail。
(3)、遍历完原始链表后,将 smallerHead 的尾节点 smallerTail 连接到 greaterHead 的头节点之后,形成新的链表。
(4)、将 greaterTail 的尾节点的 next 指针设置为 null,确保新链表的尾节点的 next 为 null。
返回新链表的头节点 smallerHead.next,即小于 x 的节点排在前面的链表的头节点。
public class Partition {
public ListNode partition(ListNode pHead, int x) {
ListNode smallerHead = new ListNode(0); // 用于存储小于 x 的节点的链表
ListNode greaterHead = new ListNode(0); // 用于存储大于等于 x 的节点的链表
ListNode smallerTail = smallerHead; // smallerTail 指向 smallerHead 的尾节点
ListNode greaterTail = greaterHead; // greaterTail 指向 greaterHead 的尾节点
while (pHead != null) {
if (pHead.val < x) {
smallerTail.next = pHead;
smallerTail = smallerTail.next;
} else {
greaterTail.next = pHead;
greaterTail = greaterTail.next;
}
pHead = pHead.next;
}
// 将两个链表连接起来
smallerTail.next = greaterHead.next;
greaterTail.next = null; // 确保最后一个节点的 next 为 null
return smallerHead.next; // 返回新链表的头指针
}
}
6、对于一个链表,请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法,判断其是否为回文结构。给定一个链表的头指针A,请返回一个bool 值,代表其是否为回文结构。保证链表长度小于等于900。
比如:1->2->2->1
要判断一个链表是否为回文结构,我们还是可以使用快慢指针和链表反转的方法:
public boolean chkPalindrome(ListNode head) {
// 1. 找到中间位置
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
//2. 开始翻转
ListNode cur = slow.next;
while(cur != null) {
ListNode curNext = cur.next;//记录一下下一个节点
cur.next = slow;
slow = cur;
cur = curNext;
}
//3. 此时翻转完成,开始判断是否回文
while(head != slow) {
if(head.val != slow.val) {
return false;
}
//分奇偶讨论
// head 和 slow 还没有相遇,但是已经形成回文,再向后移动的话,就一起向后走了
if(head.next == slow) {
return true;
}
head = head.next;
slow = slow.next;
}
return true;
}或者写成这样(几乎和前面是一毛一样的,翻转的时候改了一下名字,稍有不同,加上了详细的步骤):
(1)、使用快慢指针找到链表的中间节点。
- 初始化快指针 fast 和慢指针 slow,均指向链表的头节点 A。
- 使用循环,每次将快指针 fast 向后移动两步,慢指针 slow 向后移动一步,直到快指针 fast 到达链表尾部或倒数第二个节点。
- 如果链表长度为奇数,快指针 fast 将指向链表的最后一个节点;如果链表长度为偶数,快指针 fast 将指向空节点。
- 此时慢指针 slow 指向链表的中间节点。
(2)、反转链表的后半部分。
- 从慢指针 slow 开始,将链表的后半部分进行反转。
- 使用三个指针 prev、curr、next,进行链表的反转操作。具体步骤如下:
- 初始化 prev 为 null,curr 为 slow,next 为 null。
- 使用循环,将 curr 的下一个节点保存到 next。
- 将 curr 的下一个节点指向 prev,实现链表的反转。
- 将 prev 移动到 curr,将 curr 移动到 next,继续进行下一轮反转操作。
- 当 curr 为 null 时,表示链表的后半部分已经反转完成。
(3)、判断链表是否为回文结构。
- 从头节点 A 和反转后的链表的头节点开始,逐个比较节点的值。
- 如果有任何节点的值不相等,则链表不是回文结构,返回 false。
- 如果所有节点的值都相等,链表是回文结构,返回 true。
public boolean chkPalindrome(ListNode A) { if (A == null || A.next == null) { return true; // 链表为空或只有一个节点时,视为回文结构 } ListNode fast = A; // 快指针 ListNode slow = A; // 慢指针 // 使用快慢指针找到链表的中间节点 while (fast != null && fast.next != null) { fast = fast.next.next; slow = slow.next; } // 反转链表的后半部分 ListNode prev = null; ListNode curr = slow; ListNode next = null; while (curr != null) { next = curr.next; curr.next = prev; prev = curr; curr = next; } // 比较链表的前半部分和反转后的后半部分 ListNode left = A; // 前半部分的头节点 ListNode right = prev; // 反转后的后半部分的头节点 while (left != null && right != null) { if (left.val != right.val) { return false; // 如果节点的值不相等,则链表不是回文结构 } left = left.next; right = right.next; } return true; // 所有节点的值都相等,链表是回文结构 }
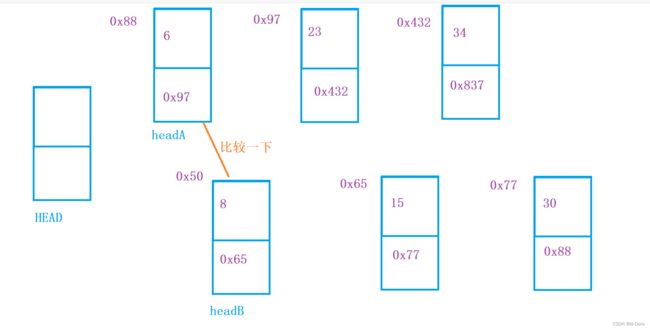
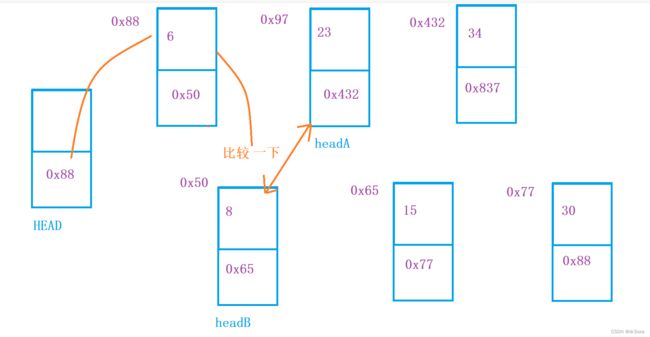
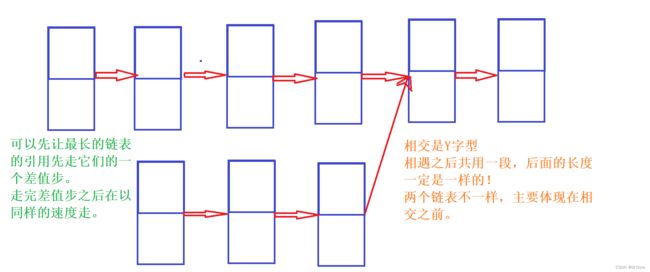
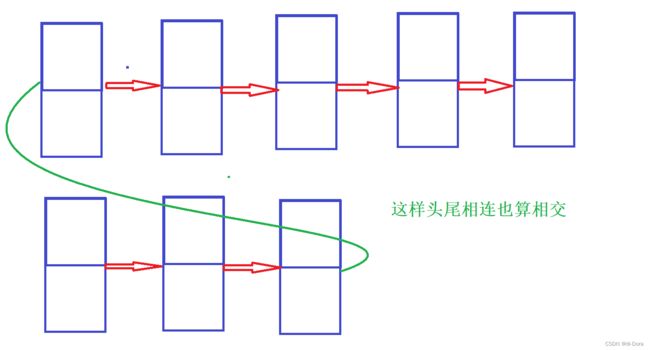
7、给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
真正的相交意味着什么?——不是 value 相同就可以了,而是形成了 Y 字型!!!
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
int lenA = getLength(headA);
int lenB = getLength(headB);
ListNode ptrA = headA;
ListNode ptrB = headB;
// 将较长的链表指针先向后移动|lenA - lenB|个位置
if (lenA > lenB) {
int diff = lenA - lenB;
while (diff > 0) {
ptrA = ptrA.next;
diff--;
}
} else if (lenB > lenA) {
int diff = lenB - lenA;
while (diff > 0) {
ptrB = ptrB.next;
diff--;
}
}
// 同时移动两个指针,寻找相交节点
while (ptrA != null && ptrB != null) {
if (ptrA == ptrB) {
return ptrA;
}
ptrA = ptrA.next;
ptrB = ptrB.next;
}
return null; // 没有相交节点,返回null
}
// 辅助函数,获取链表的长度
private int getLength(ListNode head) {
int length = 0;
ListNode ptr = head;
while (ptr != null) {
length++;
ptr = ptr.next;
}
return length;
}链表的优缺点
链表相比于数组具有以下特点和优势:
- 动态性:链表的长度可以根据需要动态地增长或缩小,不需要预先定义大小。
- 插入和删除操作效率高:由于链表的节点之间通过指针连接,插入和删除节点的操作只需要改变指针的指向,时间复杂度为O(1)。
- 空间利用效率高:链表节点在内存中分散存储,不需要连续的内存空间,可以更灵活地利用内存。
- 链表长度没有固定限制:链表的长度可以根据需要动态调整,不受固定大小的限制。
然而,链表也有一些缺点:
访问效率较低:链表中的节点不是连续存储的,访问特定位置的节点需要从头节点开始遍历,时间复杂度为O(n),其中n为链表长度。
额外的存储空间:链表中的每个节点都需要额外的指针来指向下一个节点(以及前一个节点,对于双向链表),因此需要额外的存储空间。
综上,链表适用于需要频繁插入和删除节点的场景,而不太关注访问效率。我们还是需要根据具体的应用场景和需求,选择合适的数据结构(如数组或链表),这是很重要的。