线性神经网络

线性神经网络

我们应该从线性神经网络开始，去逐步了解深度神经网络（深度学习）的各种复杂结构和底层原理。

1. 线性回归

用一个线性的模型来拟合数据与它们的标签之间的映射，用于回归问题。

1.1 构造线性模型：

$$y={\omega }^{T}x\text{\hspace{1em}(1-1)}$$

图1 线性回归与神经网络的关系

由(1-1)不难发现，线性回归其实就是单层线性神经网络。

1.2 最小二乘损失函数：

可以证明，让线性回归偏差的L2范数（均方误差）最小 等价于 对线性模型的极大似然估计…
$$L(\omega )=\sum _{i=1}^N||{\omega }^T{x}_i-y_i|{|}_2^2\text{\hspace{1em}(1-2)}$$

1.3 求解：

(1-2)是一个凸优化问题，而且比较简单，可以求得解析解。所以可以令求导=0的方式对其求解析解：
$$\omega =(X^{T}X{)}^{-1}{X}^{T}Y\text{\hspace{1em}(1-3)}$$
当然梯度下降应该能求出非常接近解析的效果…

1.4 预测：

求解出参数向量之后把x代入线性模型即可预测。

1.5 小节：

不难理解吧？最经典、古老、简单的模型了吧…

2. 线性分类

线性分类就要是把线性回归设法用于分类问题。相对于回归问题来说，变化有以下几点：

2.1 多输出

最直观的改动应该是一个输出变成多个了。我们期望用多个输出神经元来达到估计每个类别分布的目的。

图2 线性分类与神经网络的关系

2.2 输出层

搞清楚多输出的网络结构之后，输出层应该使用怎样的策略呢？对每个输出神经元应用(1-1)那样的前向传播方法来计算不可以吗？？其实不行：

因为对于分类问题，必须要使所有神经元的输出满足：

1. 均≥0
2. 和=1
3. 输出层的传递函数必须可导

对于以上3个特点，分类问题的输出层有着独特的设计——softmax激活函数：
$$y_j=\frac{e^{o_j}}{{\sum }_k^N{e}^{o^k}}\text{\hspace{1em}(2-1)}$$
(2-1)中，oj为输出层第j个【原输出】，经过这样的处理后yj为最终输出，可以保证以上三点。

softmax激活函数的具体工作方式如下图所示：

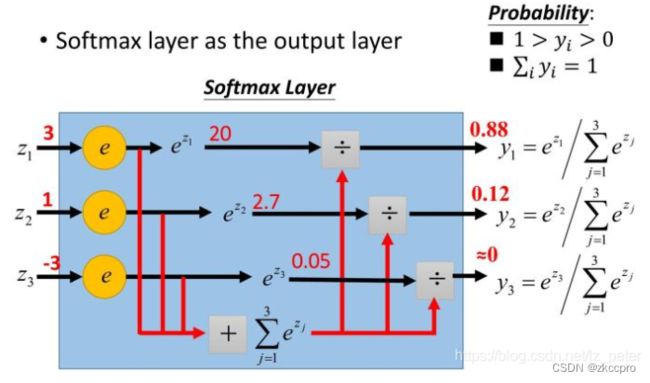
图3 由softmax激活函数连接到输出层示意

2.3 损失函数

这样搞了之后我们的损失函数采用交叉熵损失，这是由极大对数似然估计推导而来的损失函数，可以证明和MSE损失是等价的：
$$l(y,y)=-\sum _{j=1}^N{y}_{i}log{y}_i\text{\hspace{1em}(2-2)}$$
(2-2)中，y为独特编码的分类标签向量，yi为y的第i个分量。

3. 逻辑回归

逻辑回归这个名称容易造成误解。它并不是处理回归问题的，而是分类问题。经典的逻辑回归用来解决二分类问题。它需要预先估计分类数据点的分布，然后通过引入非线性函数（logistic/sigmoid）来估计把数据分为某类别的概率，输出的是概率分布函数P(y|x,θ)。

下面先以二分类举例推导：

3.1 估计数据边界（分类超平面是线性or非线性？）

一般假设它是线性的，即：
$$y={\theta }^{T}x\text{\hspace{1em}(3-1)}$$

3.2 构造预测函数：

其实就是只有两个类的softmax函数：
$$\begin{gathered} p(y=1|x,\theta )=h_{\theta }(x) \\ p(y=0|x,\theta )=1-h_{\theta }(x) \\ {h}_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}\text{\hspace{1em}(3-2)} \end{gathered}$$

3.3 构造损失函数：（极大似然估计）

$$\begin{gathered} l(x)=\sum _{i=1}^N{y}_{i}log{h}_{\theta }(x_i)+(1-y_i)log(1-h_{\theta }(x_i)) \\ J(\theta )=-\frac{l(\theta )}{m}\text{\hspace{1em}(3-3)} \end{gathered}$$

J(θ)就是极大似然函数的负对数，求J(θ)的最小值即可。