常见优化器详解
优化器
目前有两种主流优化器:随机梯度下降系(Stochastic Gradient Descent, SGD)和Adam系。
应该认识到的是,优化器并不是某类数学上的优化算法,而是梯度下降(一阶迭代法)的工程实现方案和包装。
1. 随机梯度下降系优化器
1.1 从完全梯度到随机梯度
这是最常用的一种优化器。它的思想非常巧妙。既保证了梯度下降的收敛性,又最大程度上保障了算法的时间复杂度。
先回顾一下经典的梯度下降算法公式:
θ t + 1 = θ t − α ∇ θ t L ( x , θ t ) T (1-1) θ_{t+1}=θ_t-α∇_{θ_t}L(x,θ_t )^T\tag{1-1} θt+1=θt−α∇θtL(x,θt)T(1-1)
其中,α为学习率,L(x,θ)为损失函数。注意,L可以理解为关于输入数据x和模型参数θ向量的二元函数。对于自变量θ而言,随着输入x的变化,L(θ)其实着不同的函数!(L(x1,θ)、L(x2,θ)…)
那么考虑到训练集肯定不止1个输入数据,你觉得(1-1)在实际迭代训练时应该如何计算?最简单的想法是:为了保证计算到的梯度是使用了所有训练样本的信息,梯度应该取所有样本的梯度平均值。因此,式(1-1)更新如下:
θ t + 1 = θ t − α N ∇ θ t ∑ i = 1 N L ( x i , θ t ) T (1-2) θ_{t+1}=θ_t-\frac{α}{N} ∇_{θ_t}\sum^{N}_{i=1} L(x_i,θ_t)^T\tag{1-2} θt+1=θt−Nα∇θti=1∑NL(xi,θt)T(1-2)
(1-2)就是梯度下降算法在训练时的实现。**式中N为训练集样本数量。可以保证每次更新参数时都利用了所有样本的数据。但如果训练集的规模是1k、1w、100w呢??如果优化器按(1-2)设计,训练的时间明显会随数据集规模增大而增长。即,式(1-2)是一个O(n)时间的算法(n为数据集规模)。。。这肯定是没法用的!
怎么办呢?人们发现:如果每次更新参数时的梯度仅随机挑数据集中一个样本的梯度**(随机梯度)** 和 每次更新参数把所有样本的梯度取平均(完全梯度),这两种梯度的期望是一样的!也就是说,当模型在训练集上迭代的次数足够多时,完全可以用随机梯度来代替完全梯度。
于是,我们的式(1-2)就可以变为:
θ t + 1 = θ t − α ∇ θ t L ( x i , θ t ) T , x ∈ [ 1 , N ] (1-3) θ_{t+1}=θ_t-α∇_{θ_t}L(x_i,θ_t )^T,x\in[1,N]\tag{1-3} θt+1=θt−α∇θtL(xi,θt)T,x∈[1,N](1-3)
(1-3)就是随机梯度下降法的实现。可见,当每次更新参数时,随机梯度下降在所有训练集中随机取一个样本计算梯度用来更新参数。随机梯度下降的时间复杂度是O(1)。
当然,有优点就有缺点。时间复杂度虽然降低了,但有三个问题:
- 并不一定快!
- 相比梯度下降更易受噪声数据影响。
- 对学习率的调整构成挑战。
下两节我们分别解释这三个问题,来引出随机梯度下降的两个改进实现。
1.2 批量随机梯度下降
第一点乍一看很难理解,为什么复杂度降低了实际运行还不一定快呢???这就需要你了解计算机工程的知识。
假设你的训练集规模是1w张图片,训练开始前你把他们都加载到了内存上,现在开始用梯度下降算法更新模型参数:
- CPU生成一个随机索引,需要计算索引图片的梯度,CPU向各级缓存寻址找这张图片。
- 发现缓存不命中,去内存里寻址。内存找到了图片并把图片给CPU各级缓存。
- CPU在缓存中计算该图像的梯度,更新参数。。。
- 重复步骤1-3 1w次,完成一次epoch。
这样列出来我们就不难发现随机梯度下降为什么不快了——时间浪费在步骤2。1w张图片进行1个epoch就要在内存中寻址1w次。换句话说,缓存命中率低。
那该怎么办?梯度下降一次计算所有数据的梯度时间复杂度高,随机梯度下降的缓存命中率又十分不佳…
没错,解决方案就是采取一种折中的方案,一次取一个batch的图片计算梯度平均,作为本次更新参数的依据:
θ t + 1 = θ t − α n ∇ θ t ∑ i = 1 n L ( x i , θ t ) T (1-4) θ_{t+1}=θ_t-\frac{α}{n} ∇_{θ_t}\sum^{n}_{i=1} L(x_i,θ_t)^T\tag{1-4} θt+1=θt−nα∇θti=1∑nL(xi,θt)T(1-4)
**(1-4)就是批量梯度下降的实现。**式中n为深度学习中重要的超参数之一:batch_size。按(1-4)进行计算,理论上说一次epoch的内存寻址次数至少是原来的1/batch_size,缓存不命中次数大大降低,提高了梯度计算速度。
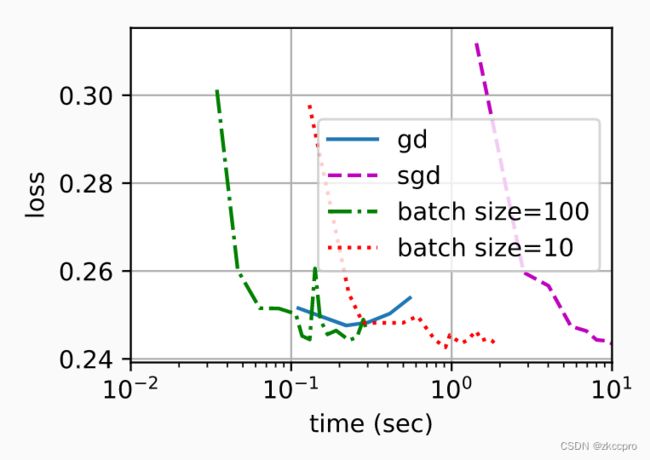
图1 目前为止三种梯度下降系算法的loss与达到时间对比
可见,sgd、b-sgd最终均可以和gd达到差不多的loss,这说明了随机梯度的方差确实和完全梯度一致(随机梯度是完全梯度的无偏估计)。但达到相同的loss,sgd甚至是最慢的。**而对于b-sgd,一定范围内,batch_size设置地越大,达到同样loss的时间越短。**这对我们选batch_size有一个很好的指示。
1.3 动量优化器
1.2节中的b-sgd方法可以解决很大一部分问题,不仅大大加快了训练速度,貌似也可以对噪声梯度有一定抑制作用。
但引入随机梯度后,学习率调整的问题对于一阶梯度 还无法解决,具体表现在两个方面:
- 对于同一参数的不同优化时期,优化效果不一致。
- 对于不同的参数,损失函数不同将导致优化效果不平衡。
先解释问题1:
在梯度下降算法中,由于每次更新几乎没有噪声梯度的干扰,训练结果可以自始至终向最优方向进发:

图2 gd方法在二元凸函数中的优化过程
但对于随机梯度下降:
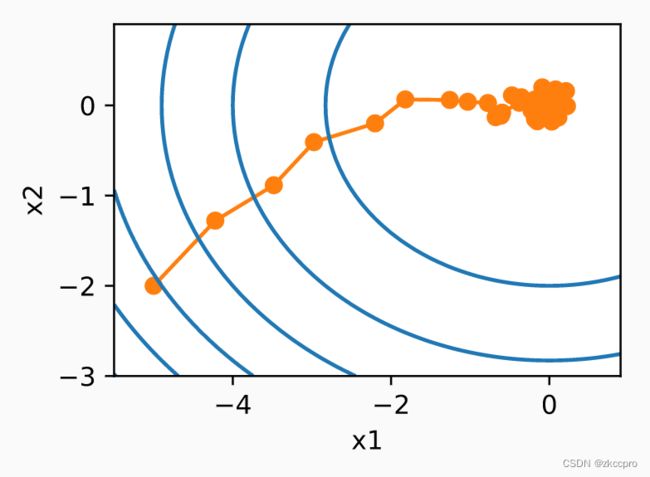
图3 sgd方法在二元凸函数中的优化过程
可见,在随机梯度的影响下,优化如此简单的凸函数有时还会往反方向走(越到优化后期这个趋势越明显)。这种现象也不难理解,优化后期随着梯度减小,任何一个小的扰动都有会放大参数更新方向的误差。不幸的是,就算引入batch的概念,这种扰动带来的影响还是不容忽视,这咋整呢???
现在广泛采用的方法是:动态调整学习率(lr_scheduler),越到后期给越小的lr,以削弱后期噪声梯度带来的影响。各个深度学习框架封装好的学习率调度器都提供很多种学习率调整方法,详见:(4条消息) 史上最全学习率调整策略lr_scheduler_cwpeng.cn的博客-CSDN博客_学习率调整(Pytorch)
接下来看问题2:对于不同的参数,损失函数不同将导致优化效果不平衡。
啥意思呢,对于参数向量θ来说,不同的分量很可能会有差别很大的梯度分布,比如简单的二元凸函数:
f ( x 1 , x 2 ) = 0.1 x 1 2 + 9 x 2 2 f(x_1, x_2)=0.1x_1^2+9x_2^2 f(x1,x2)=0.1x12+9x22
在它身上应用gd系算法的效果:

图4 不同参数间梯度分布的不平衡问题
可见,x2分量梯度非常大,而x1分量梯度则很小。于是,应用gd系算法的效果就是:x2参数很快就能达到收敛,找到最优解;而x1分量迭代了好多好多步仍然没找到最优解,进而拉低了整个训练的效果。咋整???
动量优化器对这种问题的解法就是采用【历史平均梯度(动量)】来代替原来的梯度:
v t = β v t − 1 + g t θ t + 1 = θ t − α v t (1-5) v_t=βv_{t-1}+g_{t} \\ θ_{t+1}=θ_t-αv_t\tag{1-5} vt=βvt−1+gtθt+1=θt−αvt(1-5)
(1-5)就是动量优化器的实现。
式中gt是之前任意一种计算梯度(完全梯度、随机梯度、批量梯度…)
vt就是动量
β为动量参数(简称动量)
把动量的递推公式展开写就会发现,动量近似于把过去累积的梯度求平均。
用历史平均梯度更新参数(参考图4),如果梯度较大且在最优点附近震荡(图4中x2),历史平均梯度则会相互抵消好多,可以正常收敛;而对于梯度较小的情况(图4中x1), 用历史梯度正好可以累积更大的梯度,让其加速收敛。总之,这是一种对各个参数不同梯度分布情况可以较好自适应的算法。

图5 使用动量优化器对于梯度不平衡问题的自适应效果
可见,用了动量之后,x1确实比图4收敛更快,从而总体达到更快的收敛效果。
1.4 小节
以上就是SGD优化器的全部内容了。**(1-5)式可以给产品级框架使用的SGD优化器一个完整的概述。**是否使用动量、动量参数取值、batch_size的取值、lr的取值、lr_scheduler的选取,都是便于插拔使用的。
from torch.optim import SGD
from torch.optim import lr_scheduler
optimizer = SGD(model.parameters(), lr=0.001, momentum=0.9)
scheduler=lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
2. Adam系优化器
SGD大部分情况下可以很好地解决大部分优化问题。Adam系优化器试图利用历史梯度信息对学习率做一些自适应的处理。
2.1 AdaGrad
AdaGrad认为,当前梯度大,说明当前处于优化早期阶段,此时模型获得的信息过少,不应该走的太快,应该对学习率做一个较大的惩罚;而梯度小时,说明优化已经进入后期,此时模型应该已经获得更多信息了,不应该对学习率做更大的惩罚了(但后期仍应该让lr处于下降的趋势)。
基于这种想法,他设计了如下的更新公式:
s t = s t − 1 + g t 2 θ t = θ t − 1 − α s t + ε . g t (2-1) s_t=s_{t-1}+g_t^2 \\ θ_{t}=θ_{t-1}-\frac{α}{\sqrt{s_t+\varepsilon}}. g_t\tag{2-1} st=st−1+gt2θt=θt−1−st+εα.gt(2-1)
**(2-1)就是AdaGrad的实现。**可以看到,随着优化进程进行,gt应该会逐渐变小,因此对学习率的惩罚【涨幅】会越来越小(学习率会一直下降,但下降得越来越慢)。
2.2 RMSProp
上面的AdaGrad有一个问题,就是在优化后期时,学习率由于持续受到惩罚,变得非常小,不咋动了…原因在于长时间积累的梯度过大。所以RMSProp对学习率惩罚st的积累做出约束:
s t = γ s t − 1 + ( 1 − γ ) g t 2 θ t = θ t − 1 − α s t + ε . g t (2-2) s_t=\gamma s_{t-1}+(1-\gamma)g_t^2 \\ θ_{t}=θ_{t-1}-\frac{α}{\sqrt{s_t+\varepsilon}}. g_t\tag{2-2} st=γst−1+(1−γ)gt2θt=θt−1−st+εα.gt(2-2)
**(2-2)就是RMSProp的实现。**γ一般取一个较大的值(0.9),这样每代叠加的惩罚就会比较小。到后期仍保持健康的学习率。
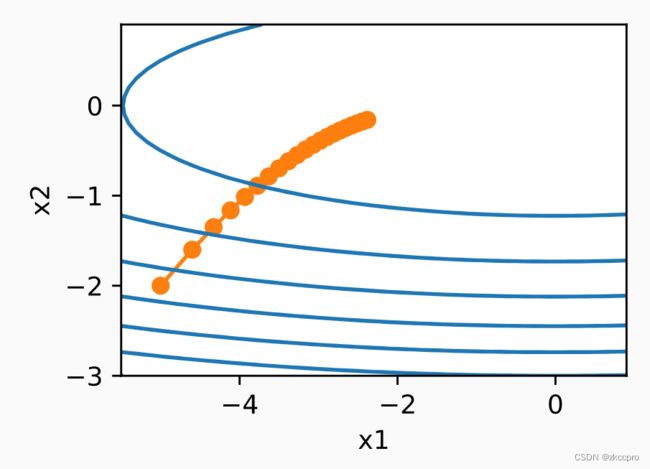
图6 AdaGrad在二元凸函数上的优化表现(α=0.4)

图7 RMSProp在二元凸函数上的优化表现(α=0.4,γ=0.9)
对比可见,在同样的学习率下,RMSProp在后期确实具有更大的学习率。
2.3 Adam
Adam是一种结合了前面几种(包括SGD中的一些)方法的一种综合实现,主要包括动量、自适应梯度惩罚:
v t = β 1 v t − 1 + ( 1 − β 1 ) g t s t = β 2 s t − 1 + ( 1 − β 2 ) g t 2 v t ^ = v t 1 − β 1 s t ^ = s t 1 − β 2 θ t = θ t − 1 − α v t ^ s t ^ + ε . g t (2-3) v_t=\beta_1 v_{t-1}+(1-\beta_1)g_t\\ s_t=\beta_2 s_{t-1}+(1-\beta_2)g_t^2 \\ \widehat{v_t}=\frac{v_t}{1-\beta_1}\\ \widehat{s_t}=\frac{s_t}{1-\beta_2}\\ θ_{t}=θ_{t-1}-\frac{α\widehat{v_t}}{\sqrt{\widehat{s_t}}+\varepsilon}. g_t\tag{2-3} vt=β1vt−1+(1−β1)gtst=β2st−1+(1−β2)gt2vt =1−β1vtst =1−β2stθt=θt−1−st +εαvt .gt(2-3)
**(2-3)就是Adam的实现。**看似有些复杂,不过仔细一看都很熟悉。第一行的动量在前面的基础上稍作系数上的改动,第二行的自适应梯度和RMSProp一样的,第三第四行是对vt和st的一个标准化,最后用【类似于】AdaGrad的方式对学习率做自适应惩罚。但是注意根号的范围,和AdaGrad的区别是不包括后面那个epsilon。
这样看,Adam的设计思想就比较清晰了,大致可以看成是引入动量的RMSProp。
2.4 小节
总得来说,Adam和SGD系的主要区别在于引入对学习率的自适应惩罚,可以根据历史梯度信息自适应调整(减小)学习率。
在使用时,SGD一般还需要引入lr_scheduler来调度学习率,但Adam自带学习率惩罚显然就没必要了,可见还是使用Adam更省心一些啊。(但我咋感觉还是SGD用得更多?)
最后要注意的是,使用Adam时,weight decay并不是传统意义上参数的L2范数正则。