二、线性神经网络
文章目录
- 前言
- 一、线性回归
-
- 1. 线性回归的基本元素
-
- 1.1 线性模型
- 1.2 损失函数
- 1.3 解析解
- 1.4 梯度下降
- 1.5 用模型进行预测
- 2. 正态分布与平方损失
- 3. 从线性回归到深度网络
- 二、线性回归的代码实现
-
- 1. 生成数据集
- 2. 读取数据集
-
- 2.1 手动实现读取数据集
- 2.2 简洁实现读取数据集
- 3. 初始化模型参数
-
- 3.1 手动初始化
- 3.2 简洁实现初始化
- 4. 定义模型
-
- 4.1 手动定义
- 4.2 简洁定义
- 5. 定义损失函数
-
- 5.1 手动定义
- 5.2 简洁定义
- 6. 定义优化算法
-
- 6.1 手动定义
- 6.2 简洁定义
- 7. 训练
-
- 7.1 手动训练
- 7.2 简洁训练
- 三、逻辑回归
-
- 3.1 二分类回归
-
- 3.1.1 二分类回归的大致流程
- 3.1.2 sigmoid函数
- 3.1.3 定义损失函数
- 3.1.4 手动代码实现
- 3.2 多分类回归
-
- 3.2.1 网络架构
- 3.2.2 大致流程
- 3.2.3 softmax函数
- 3.2.4 损失函数
- 3.2.5 避免softmax函数上溢以及对数下溢
- 3.2.6 softmax回归代码实现
- 总结
前言
在介绍深度神经网络之前,我们需要了解神经网络训练的基础知识。 本章我们将介绍神经网络的整个训练过程, 包括:定义简单的神经网络架构、数据处理、指定损失函数和如何训练模型。 为了更容易学习,我们将从经典算法————线性神经网络开始,介绍神经网络的基础知识。 经典统计学习技术中的线性回归和softmax回归可以视为线性神经网络, 这些知识将为其他部分中更复杂的技术奠定基础。
一、线性回归
1. 线性回归的基本元素
1.1 线性模型
这里先假设我们的模型是用来预测房屋价格的。设特征个数为2,分别为面积和房龄,目标是房屋价格,则可用下式表达:
p r i c e = w a r e a ⋅ a r e a + w a g e ⋅ a g e + b . \mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age} + b. price=warea⋅area+wage⋅age+b.
其中w可称为权重,用来衡量每个特征对预测值的影响程度,b称为偏置项(或偏移量、截距),偏置项可以提高模型的表达能力。
数学表达:
y ^ = w 1 x 1 + . . . + w d x d + b . \hat{y} = w_1 x_1 + ... + w_d x_d + b. y^=w1x1+...+wdxd+b.
其中 y ^ \hat{y} y^ 表示预测值,w表示权重,x表示特征值,b表示偏置项。
上式向量表示:
y ^ = w ⊤ x + b . \hat{y} = \mathbf{w}^\top \mathbf{x} + b. y^=w⊤x+b.
这是一个样本的表达式,因此这里的y是一个标量。
多个样本的表达式如下:
y ^ = X w + b {\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + \mathbf{b} y^=Xw+b
其中 y ^ \hat{\mathbf{y}} y^与w是一个一维向量, X \mathbf{X} X是一个矩阵,b是一个标量,b可通过广播机制与Xw的结果每个元素相加。
注b是可以合并在w中的,具体如下图所示:
1.2 损失函数
使用平方误差公式 作为线性回归的损失函数:
l ( i ) ( w , b ) = 1 2 ( y ^ ( i ) − y ( i ) ) 2 . l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2. l(i)(w,b)=21(y^(i)−y(i))2.
其中 i i i表示第 i i i个样本,因此所有样本的总损失函数可设为:
L ( w , b ) = 1 n ∑ i = 1 n l ( i ) ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2 . L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2. L(w,b)=n1i=1∑nl(i)(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2.
1.3 解析解
由于线性回归问题是一个很简单的优化问题,我们可以推出它的解析解,所谓解析解就是能用公式直接推出权重的值。
w ∗ = ( X ⊤ X ) − 1 X ⊤ y . \mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}. w∗=(X⊤X)−1X⊤y.
推导过程如下:
y = X w ⇒ X T y = X T X w ⇒ w = ( X T X ) − 1 X T y y = Xw\Rightarrow X^Ty = X^TXw\Rightarrow w = (X^TX)^{-1}X^Ty y=Xw⇒XTy=XTXw⇒w=(XTX)−1XTy
1.4 梯度下降
即使我们无法得到解析解,我们也可以通过梯度下降方法来优化损失函数。
梯度是指向某个函数在每一点处上升最快的方向的向量,故其反向量指向函数下降最快的方向,因此我们可利用梯度下降来求得函数的最小值,该最小值不一定是全局最小值,但对于凸函数一定是全局最小值。
我们可使用如下公式来迭代的 x \mathbf{x} x:
x = x − l r ∗ ∂ L ( w ) ∂ w \mathbf{x} = \mathbf{x} - lr * \frac{\partial L(w)}{\partial w} x=x−lr∗∂w∂L(w)
其中lr表示学习率,用来控制迭代的幅度。
根据求梯度的方式不同,梯度下降可分为如下几种:
- 批量梯度下降: 即求梯度时,使用全部样本数据来求梯度。
- 优点:全面优化,收敛快,可用向量并行计算
- 缺点:开销大,更新慢,容易陷入局部最优解
- 随机梯度下降: 随机选取一个样本进行梯度计算。
- 优点:速度快,可跳出局部最优解
- 缺点: 方向不稳定导致收敛的速度不确定,可能陷入噪声中,需要更多次迭代。
- 小批量梯度下降: 使用一部分样本进行梯度的计算。是 前两个的折中,最常用。
1.5 用模型进行预测
根据上面的步骤后,我们已经求得模型,因此我们可以使用该模型进行预测新的房价,这种行为称为预测(prediction)–更准确 或者 推断(inference)
2. 正态分布与平方损失
为什么我们可以使用均方差 来表示线性回归的损失函数呢,这里涉及到正态分布 以及最大似然函数的计算.
P ( y ∣ X ) = ∏ i = 1 n p ( y ( i ) ∣ x ( i ) ) . P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)}). P(y∣X)=i=1∏np(y(i)∣x(i)).
− log P ( y ∣ X ) = ∑ i = 1 n 1 2 log ( 2 π σ 2 ) + 1 2 σ 2 ( y ( i ) − w ⊤ x ( i ) − b ) 2 . -\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2. −logP(y∣X)=i=1∑n21log(2πσ2)+2σ21(y(i)−w⊤x(i)−b)2.
3. 从线性回归到深度网络
注:这是单层的
对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连, 我们将这种变换称为全连接层(fully-connected layer)或称为稠密层(dense layer)。
二、线性回归的代码实现
引入包:
%matplotlib inline
import random
import torch
from d2l import torch as d2l
1. 生成数据集
def synthetic_data(w, b, num_examples): #@save
"""生成y=Xw+b+噪声"""
X = torch.normal(0, 1, (num_examples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape) #加了噪声
return X, y.reshape((-1, 1)) #返回数据集 以及标签
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
2. 读取数据集
2.1 手动实现读取数据集
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
# 这些样本是随机读取的,没有特定的顺序
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(
indices[i: min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
这里我们使用的是小批量梯度下降算法。
2.2 简洁实现读取数据集
def load_array(data_arrays, batch_size, is_train=True): #@save
"""构造一个PyTorch数据迭代器"""
dataset = data.TensorDataset(*data_arrays) #返回TensorDataset类实例
return data.DataLoader(dataset, batch_size, shuffle=is_train) #shuffle表明是否乱序
batch_size = 10
data_iter = load_array((features, labels), batch_size)
3. 初始化模型参数
3.1 手动初始化
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
3.2 简洁实现初始化
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
其中net为下面简洁定义的模型。
4. 定义模型
4.1 手动定义
def linreg(X, w, b): #@save
"""线性回归模型"""
return torch.matmul(X, w) + b
4.2 简洁定义
# nn是神经网络的缩写
from torch import nn
net = nn.Sequential(nn.Linear(2, 1))
5. 定义损失函数
5.1 手动定义
def squared_loss(y_hat, y): #@save
"""均方损失"""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
5.2 简洁定义
loss = nn.MSELoss() #该loss具有求和功能
6. 定义优化算法
6.1 手动定义
def sgd(params, lr, batch_size): #@save
"""小批量随机梯度下降"""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
6.2 简洁定义
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
7. 训练
7.1 手动训练
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # X和y的小批量损失
# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,
# 并以此计算关于[w,b]的梯度
l.sum().backward()
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
7.2 简洁训练
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X) ,y)
trainer.zero_grad()
l.backward()
trainer.step()
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')
三、逻辑回归
逻辑回归即类似于分类问题,通常我们有二分类以及多分类问题,二分类我们常选用sigmoid函数,而多分类问题,我们常选用softmax函数,因此也可称为softmax回归。
3.1 二分类回归
3.1.1 二分类回归的大致流程
在上述的单层线性回归中对与每个样本我们会得到一个预测值,我们只需要把这个预测值一分为二,如果预测值在某个区域那么它就属于类别1,否则就属于类别2。 然后根据真实标签值不断的训练权重,从而实现二分类。
3.1.2 sigmoid函数
sigmoid函数的表达式为:
σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
它的图像如下:
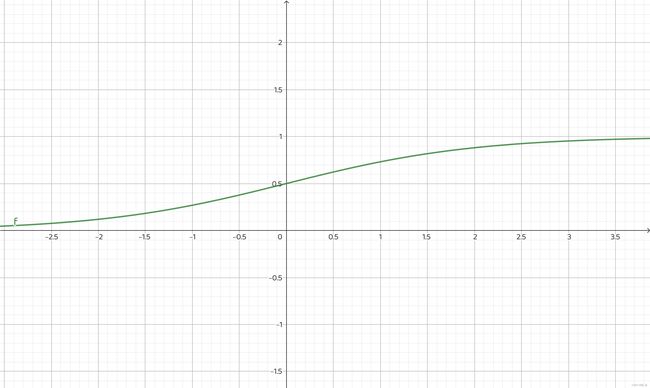
它可以把整个实数域的值映射到0到1之间,刚好0-0.5属于一类,0.5-1属于一类。
因此调整之后的公式为:
σ = 1 1 + e − X w \sigma = \frac{1}{1 + e^{-Xw}} σ=1+e−Xw1
其中 σ \sigma σ可看作属于某一类别的概率。
3.1.3 定义损失函数
设预测类别1的概率为 P 1 = σ P_1 = \sigma P1=σ,预测类别为2的概率为 P 2 = 1 − σ P_2 = 1-\sigma P2=1−σ。
在某个样本以及权重下,预测值的概率可描述为:
P ( y ^ i ∣ x i , w ) = P 1 y i ∗ P 0 1 − y i P(\hat{y}_i|x_i,w) = P^{y_i}_1 * P^{1-y_i}_0 P(y^i∣xi,w)=P1yi∗P01−yi
其中 y i y_i yi表示该样本的真实值,当其为1时, P ( y ^ i ∣ x i , w ) = P 1 P(\hat{y}_i|x_i,w) =P_1 P(y^i∣xi,w)=P1 此时若 P 1 P_1 P1越接近1越损失越小;当其为0时, P ( y ^ i ∣ x i , w ) = P 0 P(\hat{y}_i|x_i,w) =P_0 P(y^i∣xi,w)=P0 此时若 P 0 P_0 P0越接近1越损失越小。
因此总的样本概率为:
P = ∏ i = 1 m P ( y ^ i ∣ x i , w ) = ∏ i = 1 m ( P 1 y i ∗ P 0 1 − y i ) = ∏ i = 1 m ( σ i y i ∗ ( 1 − σ i ) 1 − y i ) \begin{aligned} P& =\prod\limits_{i=1}^{m}P(\hat{y}_i|x_i,w) \\ &=\prod\limits_{i=1}^m(P_1^{y_i}*P_0^{1-y_i}) \\ &=\prod\limits_{i=1}^m(\sigma_i^{y_i}*(1-\sigma_i)^{1-y_i}) \end{aligned} P=i=1∏mP(y^i∣xi,w)=i=1∏m(P1yi∗P01−yi)=i=1∏m(σiyi∗(1−σi)1−yi)
我们通常去负对数来获得损失函数:
l o s s = − ∑ i = 1 m ( y i ∗ l n ( σ i ) + ( 1 − y i ) ∗ l n ( 1 − σ i ) ) loss = -\sum\limits_{i=1}^m(y_i*ln(\sigma_i)+(1-y_i)*ln(1-\sigma_i)) loss=−i=1∑m(yi∗ln(σi)+(1−yi)∗ln(1−σi))
3.1.4 手动代码实现
import torch
from torch import nn
from torch.utils import data
num_samples = 500
num_inputs = 200
num_outputs = 1
batch_size = 20
num_epochs = 30
# 生成数据
features = torch.rand((num_samples, num_inputs), dtype=torch.float32)
labels = torch.randint(low=0, high=2, size=(num_samples, 1))
dataset = data.TensorDataset(features, labels)
train_loader = data.DataLoader(dataset, batch_size=20, shuffle=True)
# 初始化模型参数
W = torch.normal(0, 0.01, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
# 模型
def net(X, W, b):
z = torch.mm(X, W) + b
sigma = torch.sigmoid(z)
return sigma
# 损失函数
def myBCEWithLogitsLoss(outputs, labels):
loss = -(labels * torch.log(outputs) + (1 - labels) * torch.log(1 - outputs))
loss = torch.mean(loss)
return loss
# 优化算法
def sgd(W, b, lr, batch_size): # @save
"""小批量随机梯度下降"""
with torch.no_grad():
W -= lr * W.grad / batch_size
b -= lr * b.grad / batch_size
# 训练
for epoch in range(num_epochs):
for X, y in train_loader:
loss = myBCEWithLogitsLoss(net(X, W, b), y)
loss.backward()
sgd(W, b, 0.03, batch_size)
l_hat = net(features, W, b)
loss = myBCEWithLogitsLoss(l_hat, labels)
l_hat_int = torch.tensor(
[1 if l_hat[i] > 0.5 else 0 for i in range(l_hat.shape[0])]
)
accuracy = torch.mean((l_hat_int.flatten() == labels.flatten()).float())
print(f"epoch {epoch + 1}, loss {loss:f}, acc {accuracy}")
3.2 多分类回归
3.2.1 网络架构
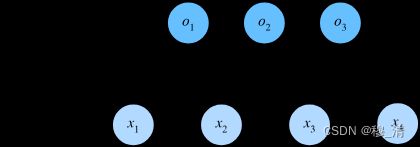
其中, o 1 = x 1 w 11 + x 2 w 12 + x 3 w 13 + x 4 w 14 + b 1 , o 2 = x 1 w 21 + x 2 w 22 + x 3 w 23 + x 4 w 24 + b 2 , o 3 = x 1 w 31 + x 2 w 32 + x 3 w 33 + x 4 w 34 + b 3 . \begin{split}\begin{aligned} o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1,\\ o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2,\\ o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3. \end{aligned}\end{split} o1o2o3=x1w11+x2w12+x3w13+x4w14+b1,=x1w21+x2w22+x3w23+x4w24+b2,=x1w31+x2w32+x3w33+x4w34+b3.
3.2.2 大致流程
O = X W + b , Y ^ = s o f t m a x ( O ) . \begin{split}\begin{aligned} \mathbf{O} &= \mathbf{X} \mathbf{W} + \mathbf{b}, \\ \hat{\mathbf{Y}} & = \mathrm{softmax}(\mathbf{O}). \end{aligned}\end{split} OY^=XW+b,=softmax(O).
先线性变换 再用softmax函数进行非线性变换。
3.2.3 softmax函数
y ^ = s o f t m a x ( o ) 其中 y ^ j = exp ( o j ) ∑ k exp ( o k ) \hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})\quad \text{其中}\quad \hat{y}_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)} y^=softmax(o)其中y^j=∑kexp(ok)exp(oj)
3.2.4 损失函数
每个样本的输出值都可以采用独热编码的方式进行表达,如进行3分类回归,若一样本对应的标签是第0分类,则其独热编码为1,0,0。
k分类损失函数推导:
P ( y ^ i ∣ x i , w ) = P 1 y i ( k − 1 ) ∗ P 2 y i ( n − 2 ) ∗ P 3 y i ( k − 3 ) ∗ … ∗ P K y i ( k − K ) P(\hat{y}_{i}|x_{i},w)=P_{1}^{y_i(k-1)}*P_{2}^{y_i(n-2)}*P_{3}^{y_i(k-3)}*\ldots*P_{K}^{y_i(k-K)} P(y^i∣xi,w)=P1yi(k−1)∗P2yi(n−2)∗P3yi(k−3)∗…∗PKyi(k−K)
取负对数可得损失函数为:
l ( y , y ^ ) = − ∑ j = 1 q y j log y ^ j . l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j. l(y,y^)=−j=1∑qyjlogy^j.
其中,q表示样本数 y j y_j yj是一个长度为k独热编码, y ^ j \hat{y}_j y^j也是一个长度为k的向量,每一个值为该类别的概率。
此损失函数称为交叉熵损失函数
3.2.5 避免softmax函数上溢以及对数下溢
由于softmax中有指数函数,容易造成数值上溢,解决办法:
y ^ j = exp ( o j − max ( o k ) ) exp ( max ( o k ) ) ∑ k exp ( o k − max ( o k ) ) exp ( max ( o k ) ) = exp ( o j − max ( o k ) ) ∑ k exp ( o k − max ( o k ) ) . \begin{split}\begin{aligned} \hat y_j & = \frac{\exp(o_j - \max(o_k))\exp(\max(o_k))}{\sum_k \exp(o_k - \max(o_k))\exp(\max(o_k))} \\ & = \frac{\exp(o_j - \max(o_k))}{\sum_k \exp(o_k - \max(o_k))}. \end{aligned}\end{split} y^j=∑kexp(ok−max(ok))exp(max(ok))exp(oj−max(ok))exp(max(ok))=∑kexp(ok−max(ok))exp(oj−max(ok)).
但此做法,可能会导致其值接近0,从而导致下溢,并且导致交叉熵损失函数中的取对数导致负无穷从而又上溢,解决办法:把两者结合
log ( y ^ j ) = log ( exp ( o j − max ( o k ) ) ∑ k exp ( o k − max ( o k ) ) ) = log ( exp ( o j − max ( o k ) ) ) − log ( ∑ k exp ( o k − max ( o k ) ) ) = o j − max ( o k ) − log ( ∑ k exp ( o k − max ( o k ) ) ) . \begin{split}\begin{aligned} \log{(\hat y_j)} & = \log\left( \frac{\exp(o_j - \max(o_k))}{\sum_k \exp(o_k - \max(o_k))}\right) \\ & = \log{(\exp(o_j - \max(o_k)))}-\log{\left( \sum_k \exp(o_k - \max(o_k)) \right)} \\ & = o_j - \max(o_k) -\log{\left( \sum_k \exp(o_k - \max(o_k)) \right)}. \end{aligned}\end{split} log(y^j)=log(∑kexp(ok−max(ok))exp(oj−max(ok)))=log(exp(oj−max(ok)))−log(k∑exp(ok−max(ok)))=oj−max(ok)−log(k∑exp(ok−max(ok))).
3.2.6 softmax回归代码实现
import torch
from torch import nn
from d2l import torch as d2l
# 获取数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
##定义模型
# PyTorch不会隐式地调整输入的形状。因此,
# 我们在线性层前定义了展平层(flatten),来调整网络输入的形状,softmax无需加
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
## 初始化参数
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
# 定义损失函数 已经融入softmax
loss = nn.CrossEntropyLoss(reduction="none")
# 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
# 训练
num_epochs = 10
if __name__ == "__main__":
for epoch in range(num_epochs):
acc = 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y)
trainer.zero_grad()
l.mean().backward()
trainer.step()
print(l.mean())
总结
本节主要讲解了线性回归以及逻辑回归及其代码实现,两者都是单层神经网络,下章将讲解多层感知机。

