基于R语言的方差分析及多重比较

主要介绍agricolae包、DescTools包、bruceR包。

agricolae

iris%>%aov(Sepal.Length~Species,data=.)%>%
  agricolae::duncan.test("Species",group=F,console=T)

group=T则输出分组标记（abc），否则输出差异值。

Study: . ~ "Species"

Duncan's new multiple range test
for Sepal.Length 

Mean Square Error:  0.2650082 

Species,  means

           Sepal.Length       std  r Min Max
setosa            5.006 0.3524897 50 4.3 5.8
versicolor        5.936 0.5161711 50 4.9 7.0
virginica         6.588 0.6358796 50 4.9 7.9

Alpha: 0.05 ; DF Error: 147 

Critical Range
        2         3 
0.2034688 0.2141585 

Means with the same letter are not significantly different.

           Sepal.Length groups
virginica         6.588      a
versicolor        5.936      b
setosa            5.006      c

双因素方差分析

library(agricolae)
data(greenhouse)
  greenhouse%>%.[[1]]%>%
    as_tibble()%>%
    split(.$method)%>%
    map(~aov(weight ~ variety,data=.x))%>%
    map(~duncan.test(.,"variety",console=F))%>%
    map(~.$groups)

>   greenhouse%>%.[[1]]%>%
+     as_tibble()%>%
+     split(.$method)%>%
+     map(~aov(weight ~ variety,data=.x))%>%
+     map(~duncan.test(.,"variety",console=F))%>%
+     map(~.$groups)
$aeroponic
            weight groups
Mariva    95.35625      a
Unica     88.54750      a
Costanera 40.15250      b

$bed
           weight groups
Mariva    96.8025      a
Costanera 87.5475     ab
Unica     69.0825      b

$hydroponic
            weight groups
Unica     26.28500      a
Costanera 26.13500      a
Mariva    14.25125      b

$pot
            weight groups
Costanera 141.0425      a
Unica      94.5550      b
Mariva     92.2050      b

DescTools

agricolae::greenhouse[[1]]%>%aov(weight ~ variety+method, data=.)%>%
  DescTools::PostHocTest(method = "duncan")

> greenhouse[[1]]%>%aov(weight ~ variety+method, data=.)%>%
+   DescTools::PostHocTest(method = "duncan")

  Posthoc multiple comparisons of means : Duncan's new multiple range test 
    95% family-wise confidence level

$variety
                      diff     lwr.ci    upr.ci   pval    
Mariva-Costanera  0.934375  -8.579594 10.448344 0.8471    
Unica-Costanera  -4.101875 -13.615844  5.412094 0.3973    
Unica-Mariva     -5.036250 -15.052430  4.979930 0.3306    

$method
                           diff     lwr.ci    upr.ci    pval    
bed-aeroponic          9.792083  -1.193702  20.77787  0.0805 .  
hydroponic-aeroponic -52.461667 -63.447452 -41.47588 3.3e-11 ***
pot-aeroponic         34.582083  23.016394  46.14777 2.0e-09 ***
hydroponic-bed       -62.253750 -73.819439 -50.68806 1.7e-11 ***
pot-bed               24.790000  13.804215  35.77579 1.2e-05 ***
pot-hydroponic        87.043750  75.090244  98.99726 1.1e-11 ***

---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

bruceR

关于bruceR包的具体内容可参考包寒吴霜的专栏。

1. 回归分析

model=lm(Temp ~ Month + Day + Wind + Solar.R, data=airquality)
GLM_summary(model)

查看结果为：

> GLM_summary(model)
MODEL INFO:
Model type: General Linear Model (GLM) (OLS Regression)
Observations: N = 146 (7 missing cases deleted)

MODEL FIT:
F(4, 141) = 22.22, p < 1e-10 ***
R² = 0.38659 (Adjusted R² = 0.36919)

ANOVA table:
─────────────────────────────────────────────────────
             Sum Sq  Df Mean Sq     F     p     η²p
─────────────────────────────────────────────────────
[Model]     4040.28   4 1010.07 18.82 <.001 *** 0.348
Month       1367.28   1 1367.28 25.47 <.001 *** 0.153
Day           76.54   1   76.54  1.43  .234     0.010
Wind        1741.28   1 1741.28 32.44 <.001 *** 0.187
Solar.R      855.18   1  855.18 15.93 <.001 *** 0.102
Residuals   7568.88 141   53.68                      
Total      11609.16 145   80.06                      
─────────────────────────────────────────────────────

FIXED EFFECTS:
Outcome variable: Temp (N = 146)
──────────────────────────────────────────────────────────────────
                  b    S.E.     t     p        [95%      CI]   VIF
──────────────────────────────────────────────────────────────────
(Intercept)  68.770 (4.391) 15.66 <.001 *** [60.089, 77.450]      
Month         2.225 (0.441)  5.05 <.001 *** [ 1.353,  3.096] 1.035
Day          -0.084 (0.070) -1.19  .234     [-0.222,  0.055] 1.024
Wind         -1.003 (0.176) -5.70 <.001 *** [-1.352, -0.655] 1.032
Solar.R       0.027 (0.007)  3.99 <.001 *** [ 0.014,  0.041] 1.034
──────────────────────────────────────────────────────────────────

Standardized coefficients: Temp (N = 146)
─────────────────────────────────────────────────────────────
          Beta*   S.E.*        [95%      CI] r.partial r.part
─────────────────────────────────────────────────────────────
Month     0.339 (0.067) *** [ 0.206,  0.471]     0.391  0.333
Day      -0.080 (0.067)     [-0.212,  0.052]    -0.100 -0.079
Wind     -0.382 (0.067) *** [-0.514, -0.249]    -0.432 -0.376
Solar.R   0.268 (0.067) *** [ 0.135,  0.400]     0.319  0.263
──────────────────────────────────────────────────────────

上述结果主要有如下几个部分：

• 拟合优度分析
• 方差分析
• 偏回归系数
• 标准化偏回归系数

下面就主要的几个参数进行解释：

决定系数$R^2$

决定系数$R^2$为复相关系数R（$y_i$与其估计值$\hat{y}$的pearson相关系数）的平方值。决定系数为模型的可解释的变异SSR占总变异SS的比例。

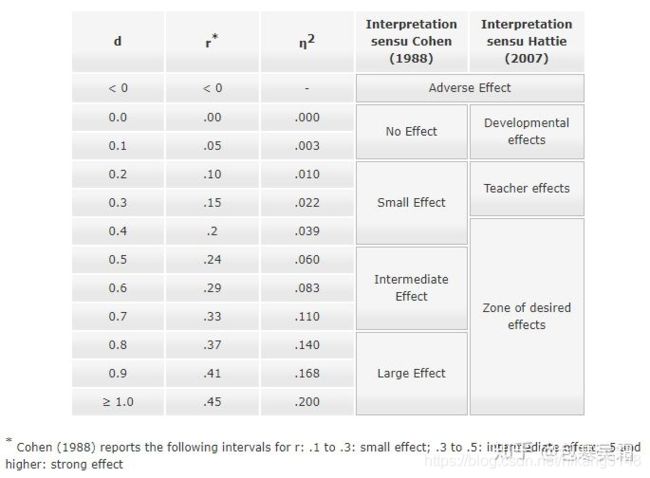
效应值η²p

变量的效应值。标准化的效应量可以分为三大家族：d-family（difference family）：如Cohen’s d、Hedges’ gr-family（correlation family）：如Pearson r、R²、η²、ω²、fOR-family（categorical family）：如odds ratio (OR)、risk ratio (RR)

方差膨胀系数VIF

方差膨胀系数VIF，表示自变量间的共线性程度，其值为容忍度的倒数，容忍度（小于1）为1减去以改自变量为因变量，其余自变量为自变量的线性模型的决定系数，可以预见如果该自变量与其余自变量存在强线性关系（决定系数越大），则其容忍度越低，而VIF值（大于1）则越大。一般认为VIF不应大于5~10。

标准化偏回归系数

标准化偏回归系数（beta）可以理解为变量的敏感度，即自变量每变化1个标准差$s{d}_x$，因变量变化beta个标准差$s{d}_y$。偏回归系数大的自变量其标准化偏回归系数不一定大。

偏相关r.partial与半偏相关r.part

partial correlations和semi-partial (part)correlations适用于研究消除其他变量的前提下两变量的相关性。具体来说：

• partial correlations是指在消除了其他所有随机变量影响的条件下，考察两变量之间的相关性。
• semi-partial (part) correlations是指在消除了其他变量对两变量部分影响的条件下(如只消除对其中一个变量的影响)，考察两变量之间的相关性。
• R语言ppcor这个包可以计算pcor()与spcor()

1. Partial Correlation

We measure individual differences in many things, including cognitive ability, personality, interests & motives, attitudes, and so forth. Many times, we want to know about the influence of one IV on a DV, but one or more other IVs pose an alternative explanation. We would like to hold some third variable constant while examining the relations between X and Y. With assignment we can do this by design. With measures of individual differences, we can do this statistically rather than by manipulation.

The basic idea in partial and semipartial correlation is to examine the correlations among residuals (errors of prediction). If we regress variable X on variable Z, then subtract X’ from X, we have a residual e. This e will be uncorrelated with Z, so any correlation X shares with another variable Y cannot be due to Z.

2. Semipartial Correlation

With partial correlation, we find the correlation between X and Y holding Z constant for both X and Y. Sometimes, however, we want to hold Z constant for just X or just Y. In that case, we compute a semipartial correlation. A partial correlation is computed between two residuals. A semipartial is computed between one residual and another raw or unresidualized variable. The notation r1(2.3) means the semipartial correlation between unmodified X1 and residualized X2, where X3 has been taken from X2.

2. 方差分析

dat2<-data.frame(Nrate=rep(rep(c(30,60,90),each=10),10), 
                   Ntype=rep(rep(c("CK","NI"),each=10),15),
                   plots=rep(1:30,each=10),
                   days=rep(1:10,30),
                   flux=runif(300,10,100)) 
  

MANOVA(data=dat2, subID="plots",
       dv="flux",
       between=c("Nrate","Ntype"),
       within="days",
       sph.correction = "GG"
       ) %>%
  EMMEANS("Ntype", by="Nrate")

• cov可设置协变量，为协方差分析。
• sph.correction参数为df校正，当球形假设不满足时，需要设置该参数。

Sphericity correction method to adjust the degrees of freedom (df) when the sphericity assumption is violated. Default is “none”. If Mauchly’s test of sphericity is significant, you may set it to “GG” (Greenhouse-Geisser) or “HF” (Huynh-Feldt).

描述分析结果

====== MANOVA Output (Mixed Design) ======

Descriptive Statistics:
───────────────────────────────
 Nrate Ntype days  Mean  S.D. N
───────────────────────────────
    30    CK   1  65.08 22.19 5
    30    CK   2  53.67 24.15 5
    30    CK   3  57.90 24.34 5
    30    CK   4  39.94 21.58 5
   。。。省略。。。。。
───────────────────────────────
Total sample size: N = 30

方差表

Contrasts set to contr.sum for the following variables: Nrate, Ntype
ANOVA Table:
Dependent variable(s):      flux
Between-subjects factor(s): Nrate, Ntype
Within-subjects factor(s):  days
Covariate(s):               -
───────────────────────────────────────────────────────────────────────────────────
                        MS     MSE   df1    df2    F     p      η²p   [90%     CI]
───────────────────────────────────────────────────────────────────────────────────
Nrate              159.853 596.670  2.00  24.00 0.27  .767     0.022 [0.000, 0.116]
Ntype              251.099 596.670  1.00  24.00 0.42  .523     0.017 [0.000, 0.166]
Nrate:Ntype        178.611 596.670  2.00  24.00 0.30  .744     0.024 [0.000, 0.124]
days              1258.718 976.600  6.63 159.16 1.29  .261     0.051 [0.000, 0.077]
Nrate:days        1029.677 976.600 13.26 159.16 1.05  .403     0.081 [0.000, 0.077]
Ntype:days         624.971 976.600  6.63 159.16 0.64  .714     0.026 [0.000, 0.034]
Nrate:Ntype:days   936.235 976.600 13.26 159.16 0.96  .495     0.074 [0.000, 0.067]
───────────────────────────────────────────────────────────────────────────────────
MSE = Mean Square Error (an estimate of the population variance σ²)
Sphericity correction method: GG (Greenhouse-Geisser)

ANOVA Effect Size:
                      ω2      η2   η2[G]   η2[p] Cohen's f
Nrate             -0.005   0.002   0.002   0.022     0.150
Ntype             -0.002   0.001   0.001   0.017     0.132
Nrate:Ntype       -0.005   0.002   0.002   0.024     0.157
days               0.009   0.040   0.047   0.051     0.232
Nrate:days         0.003   0.065   0.074   0.081     0.297
Ntype:days        -0.011   0.020   0.024   0.026     0.163
Nrate:Ntype:days  -0.003   0.059   0.068   0.074     0.283

ω² = omega-squared = (SS - df1 * MSE) / (SST + MSE)
η² = eta-squared = SS / SST
η²G = generalized eta-squared (see Olejnik & Algina, 2003)
η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
Cohen’s f = sqrt( η²p / (1 - η²p) )

方差一致性检验

Levene’s Test for Homogeneity of Variance:
DV = flux:
                Levene's F df1 df2     p sig
Based on Mean         0.58   5 294  .713    
Based on Median       0.48   5 294  .790    

球形检验

Mauchly’s Test of Sphericity:
                 Mauchly's W       p
days                 0.11454 0.44742
Nrate:days           0.11454 0.44742
Ntype:days           0.11454 0.44742
Nrate:Ntype:days     0.11454 0.44742

球形检验的结果，由于交互作用的水平数都大于2，需要进行球形检验。当球形检验的p 值大于0.05时，自变量各水平之间都符合球形假设，即相互独立。反之则表明不符合球形假设，需要参考第三个表Sphericity Corrections中的GGe（Greenhouse-Geisser epsilon）或者HFe（Huynh-Feldt epsilon）对df 进行校正。关于采取哪种校正方案， Girden (1992)认为当epsilon > 0.75时，建议用Huynh-Feldt校正，当epsilon < 0.75时，建议用Greenhouse-Geisser校正。Mauchly’s Test表的结果显示，均满足球形假设，如果不满足，需要根据Sphericity Corrections 中的GGe对交互作用的df 进行校正。

简单效应

------ EMMEANS Output (effect = "Ntype") ------

Simple Effects of "Ntype":
Nrate = 30:
 ----       df1 df2    F         p sig   η2p  [90%     CI] 
 Ntype        1  24 0.20 0.6597489     0.008 [0.000, 0.136]
 days         9  24 1.94 0.0950746 .   0.420 [0.000, 0.446]
 Ntype:days   9  24 0.31 0.9631948     0.105 [0.000, 1.000]

Nrate = 60:
 ----       df1 df2    F         p sig   η2p  [90%     CI] 
 Ntype        1  24 2.23 0.1482685     0.085 [0.000, 0.278]
 days         9  24 0.95 0.5045090     0.262 [0.000, 0.259]
 Ntype:days   9  24 1.37 0.2574159     0.339 [0.000, 0.355]

Nrate = 90:
 ----       df1 df2    F         p sig   η2p  [90%     CI] 
 Ntype        1  24 3.61 0.0693981 .   0.131 [0.000, 0.331]
 days         9  24 1.61 0.1686279     0.376 [0.000, 0.398]
 Ntype:days   9  24 2.84 0.0197606 *   0.516 [0.061, 0.545]

Estimated Marginal Means of "Ntype":
Nrate = 30:
 Ntype EM.Mean    S.E. df  [95%     CI] 
 CK      52.18 (3.650) 24 [44.65, 59.71]
 NI      54.48 (3.650) 24 [46.95, 62.01]

Nrate = 60:
 Ntype EM.Mean    S.E. df  [95%     CI] 
 CK      58.41 (3.650) 24 [50.88, 65.94]
 NI      50.70 (3.650) 24 [43.17, 58.23]

Nrate = 90:
 Ntype EM.Mean    S.E. df  [95%     CI] 
 CK      50.84 (3.650) 24 [43.31, 58.37]
 NI      60.65 (3.650) 24 [53.12, 68.18]

Results are averaged over the levels of: days 
EM.Mean uses an equally weighted average. 

Pairwise Comparisons of "Ntype":
Nrate = 30:
 Contrast     b    S.E. df     t     p sig  Cohen's d  [95%     CI]
 NI - CK   2.30 (5.162) 24  0.45  .660      0.0891568 [-0.32, 0.50]

Nrate = 60:
 Contrast     b    S.E. df     t     p sig  Cohen's d  [95%     CI]
 NI - CK  -7.71 (5.162) 24 -1.49  .148     -0.2987534 [-0.71, 0.11]

Nrate = 90:
 Contrast     b    S.E. df     t     p sig  Cohen's d  [95%     CI]
 NI - CK   9.81 (5.162) 24  1.90  .069 .    0.3801680 [-0.03, 0.79]

SD_pooled for computing Cohen’s d: 25.81 
Results are averaged over the levels of: days 
No need to adjust p values.