机器学习之线性回归模型

1 线性回归模型介绍

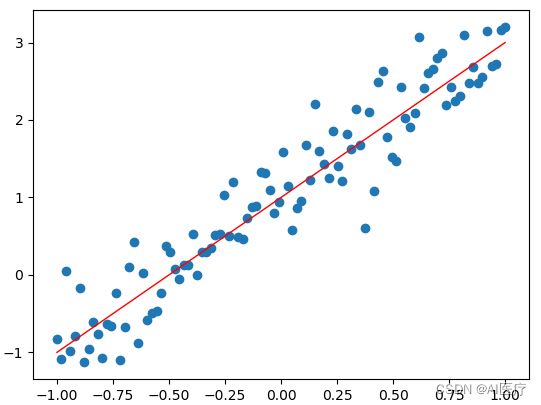
        线性回归模型是机器学习中非常基础且经典的模型，是利用线性拟合的方式探寻数据背后的规律，特征变量的个数可将线性回归模型分为一元线性回归和多元线性回归。

（1）一元线性回归

        线性模型的原型为一元一次方程，“元”的概念就是指自变量个数，线性回归是先通过搭建线性回归模型寻找样本点背后的趋势线（也称回归曲线），再利用回归曲线进行一些简单的预测分析或因果关系分析。

        一元线性回归模型是一种用于预测一个自变量和一个因变量之间关系的统计模型。它假设自变量和因变量之间存在线性关系，可以通过线性方程来表示。在一元线性回归模型中，我们有一个自变量（通常表示为x）和一个因变量（通常表示为y）。模型假设自变量x对因变量y的影响是线性的，可以用以下方程表示：

        y = ax + b

其中，y是因变量，x是自变量，b是截距，a是自变量x的系数。截距β0表示当自变量x为0时，因变量y的值。系数a表示自变量x每增加一个单位对因变量y的影响。

        线性回归的目标是通过拟合数据来估计出最优的截距和系数，使得预测值与实际观测值之间的误差最小化。这通常使用最小二乘法来实现，即最小化实际观测值与预测值之间的残差平方和。一旦模型参数估计完成，就可以使用该模型进行预测。给定一个新的自变量x，可以使用估计的截距和系数来计算因变量y的预测值。

        需要注意的是，一元线性回归模型的应用有一些前提假设，包括线性关系、误差项的独立性、误差项的方差恒定等。在使用该模型进行分析时，需要验证这些假设是否成立，并对模型的结果进行解释和评估。

（2）多元线性回归

        在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。因此多元线性回归比一元线性回归的实用意义更大。

        多元线性回归是一种用于预测一个因变量与多个自变量之间关系的统计模型。它是对一元线性回归的扩展，可以同时考虑多个自变量对因变量的影响。在多元线性回归模型中，我们有一个因变量（通常表示为y）和多个自变量（通常表示为x1, x2, ..., xn）。模型假设这些自变量与因变量之间存在线性关系，可以用以下方程表示：

        y = a1x1 + a2x2 + ... + anxn + b

其中，y是因变量，x1, x2, ..., xn是自变量，b是截距，a1, a2, ..., an是各自变量的系数。截距b表示当所有自变量都为0时，因变量y的值。系数a1, a2, ..., an表示各自变量对因变量的影响。

        多元线性回归的目标是通过拟合数据来估计出最优的截距和系数，使得预测值与实际观测值之间的误差最小化。这同样使用最小二乘法来实现，最小化实际观测值与预测值之间的残差平方和。一旦模型参数估计完成，就可以使用该模型进行预测。给定一组新的自变量x1, x2, ..., xn，可以使用估计的截距和系数来计算因变量y的预测值。

        与一元线性回归类似，多元线性回归也有一些前提假设，包括线性关系、误差项的独立性、误差项的方差恒定等。在使用该模型进行分析时，需要验证这些假设是否成立，并对模型的结果进行解释和评估。同时，还可以通过评估系数的显著性和模型的拟合优度来评估模型的有效性。

2 线性回归模型实现波士顿房价预测案例

        波士顿房价预测是一个经典的机器学习问题，可以使用线性回归模型进行预测。在波士顿房价预测问题中，我们需要根据一组特征来预测房屋的价格。

（1）数据集加载

from sklearn import datasets
import pandas as pd

bsd_dataset = datasets.load_boston()
data_df = pd.DataFrame(bsd_dataset.data, columns=bsd_dataset.feature_names)

data_df['price'] = bsd_dataset.target
print(data_df.head(10))

显示的数据结果如下：

      CRIM    ZN  INDUS  CHAS    NOX  ...    TAX  PTRATIO       B  LSTAT  price
0  0.00632  18.0   2.31   0.0  0.538  ...  296.0     15.3  396.90   4.98   24.0
1  0.02731   0.0   7.07   0.0  0.469  ...  242.0     17.8  396.90   9.14   21.6
2  0.02729   0.0   7.07   0.0  0.469  ...  242.0     17.8  392.83   4.03   34.7
3  0.03237   0.0   2.18   0.0  0.458  ...  222.0     18.7  394.63   2.94   33.4
4  0.06905   0.0   2.18   0.0  0.458  ...  222.0     18.7  396.90   5.33   36.2
5  0.02985   0.0   2.18   0.0  0.458  ...  222.0     18.7  394.12   5.21   28.7
6  0.08829  12.5   7.87   0.0  0.524  ...  311.0     15.2  395.60  12.43   22.9
7  0.14455  12.5   7.87   0.0  0.524  ...  311.0     15.2  396.90  19.15   27.1
8  0.21124  12.5   7.87   0.0  0.524  ...  311.0     15.2  386.63  29.93   16.5
9  0.17004  12.5   7.87   0.0  0.524  ...  311.0     15.2  386.71  17.10   18.9

（2）数据归一化

from sklearn.preprocessing import MinMaxScaler
X=bsd_dataset.data
Y=bsd_dataset.target

#数据归一化
X=MinMaxScaler().fit_transform(X)
data_df = pd.DataFrame(X, columns=bsd_dataset.feature_names)
print(data_df.head(10))

归一化后的数据

       CRIM     ZN     INDUS  CHAS  ...       TAX   PTRATIO         B     LSTAT
0  0.000000  0.180  0.067815   0.0  ...  0.208015  0.287234  1.000000  0.089680
1  0.000236  0.000  0.242302   0.0  ...  0.104962  0.553191  1.000000  0.204470
2  0.000236  0.000  0.242302   0.0  ...  0.104962  0.553191  0.989737  0.063466
3  0.000293  0.000  0.063050   0.0  ...  0.066794  0.648936  0.994276  0.033389
4  0.000705  0.000  0.063050   0.0  ...  0.066794  0.648936  1.000000  0.099338
5  0.000264  0.000  0.063050   0.0  ...  0.066794  0.648936  0.992990  0.096026
6  0.000921  0.125  0.271628   0.0  ...  0.236641  0.276596  0.996722  0.295254
7  0.001554  0.125  0.271628   0.0  ...  0.236641  0.276596  1.000000  0.480684
8  0.002303  0.125  0.271628   0.0  ...  0.236641  0.276596  0.974104  0.778146
9  0.001840  0.125  0.271628   0.0  ...  0.236641  0.276596  0.974305  0.424117

（3）划分训练集和测试集

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Y, random_state = 0)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

划分后的结果

(379, 13) (127, 13) (379,) (127,)

（4）启动训练

x=torch.tensor(X_train,dtype=torch.float32).T
y=torch.tensor(y_train,dtype=torch.float32)

w1=torch.randn((10,13),requires_grad=True)
w2=torch.randn((1,10),requires_grad=True)

epochs=2000
learning_rate=0.01

plt_epoch=[]
plt_loss=[]

for epoch in range(epochs):
    #计算隐藏层
    hidden=w1.mm(x)

    #加入激活函数
    hidden=torch.relu(hidden)

    #预测结果
    predictions=w2.mm(hidden)

    #损失函数
    loss=torch.mean((predictions-y)**2)

    plt_epoch.append(epoch)
    plt_loss.append(loss.item())

    #打印损失值
    if epoch%100==0:
        print('epoch:',epoch,'loss:',loss.item())

    #反向传播
    loss.backward()

    #更新权重
    w1.data-=w1.grad*learning_rate
    w2.data-=w2.grad*learning_rate

    #记得清空梯度，不然会一直累加
    w1.grad.zero_()
    w2.grad.zero_()

#绘制迭代次数与损失函数的关系
import matplotlib.pyplot as plt
plt.plot(plt_epoch,plt_loss)
plt.show()

结果输出

epoch: 0 loss: 593.4494018554688
epoch: 100 loss: 22.972753524780273
epoch: 200 loss: 23.377593994140625
epoch: 300 loss: 19.176700592041016
epoch: 400 loss: 18.216825485229492
epoch: 500 loss: 15.251435279846191
epoch: 600 loss: 14.864448547363281
epoch: 700 loss: 13.524547576904297
epoch: 800 loss: 12.281590461730957
epoch: 900 loss: 11.839076042175293
epoch: 1000 loss: 11.74725341796875
epoch: 1100 loss: 11.918133735656738
epoch: 1200 loss: 11.595450401306152
epoch: 1300 loss: 10.907296180725098
epoch: 1400 loss: 10.708924293518066
epoch: 1500 loss: 10.780670166015625
epoch: 1600 loss: 10.737732887268066
epoch: 1700 loss: 11.010161399841309
epoch: 1800 loss: 9.786482810974121
epoch: 1900 loss: 10.003388404846191

（5）测试集验证

#测试数据
x_t=torch.tensor(X_test,dtype=torch.float32).T
y_t=torch.tensor(y_test,dtype=torch.float32)

hidden=w1.mm(x_t)
hidden=torch.relu(hidden)

#预测结果
predictions=w2.mm(hidden)

#损失函数
loss=torch.mean((predictions-y_t)**2)
print('loss:',loss.detach().item())

输出结果：

loss: 23.49477195739746

3 完整代码

详见：代码下载