图卷积网络概述笔记

开一个博客把基础概念给记录下来，随笔瞎记呗

谱方法

谱方法在谱域定义卷积操作，把图变换到谱域进行卷积之后再变换到图域。
给定无向图G=(V,E,W)，点集V（n=|V|)，边集E，权带权邻接矩阵$W\in R^{n\times n}$，或者就是邻接矩阵$A\in R^{n\times n}$。每个节点如果有d维特征，所有节点的特征矩阵就是$X\in R^{n\times d}$

图的拉普拉斯矩阵：L=D-W或者L=D-A，D是度矩阵${\mathbf{D}}_{ii}={\sum }_j\left({\mathbf{A}}_{i,j}\right)$，拉普拉斯矩阵定义了图上的导数（信号的平滑程度），进一步地 normalized graph laplacian：
$$\mathbf{L}=\mathbf{I}-{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}$$

I是单位阵，L矩阵是实对称半正定矩阵就可以进行矩阵分解：$L=U\Lambda U^T$，其中$\mathbf{U}=\left[{\mathbf{u}}_1,{\mathbf{u}}_2,\cdots ,{\mathbf{u}}_{\mathbf{n}}\right]\in {\mathbf{R}}^{n\times n}$，就是特征向量矩阵；而$\Lambda$是特征值的对角矩阵$\Lambda =\mathrm{diag}\left(\left[{\lambda }_1,\cdots ,{\lambda }_n\right]\right)$，这一组特征向量相互正交（$U^{T}U=1$)，把这些特征向量作为一组正交基，对图信号$x\in R^n$进行傅里叶变换：$\mathbf{x}={\mathbf{U}}^T\mathbf{x}$，对应反变换：$\mathbf{x}=\mathbf{U}\mathbf{x}$。
对于输入信号$x\in R^n$，滤波器$g\in R^n$的卷积操作就可以在谱域下定义为：
$$x{\ast }_{G}y=U\left(\left({\mathbf{U}}^T\mathbf{x}\right)\odot \left({\mathbf{U}}^{T}g\right)\right)$$

$\odot$表示点乘，而${\mathbf{U}}^T\mathbf{x}\in R^{n\times 1}$，可以设${\mathbf{U}}^{T}g={\left[{\mathbf{\theta }}_1,\cdots ,{\mathbf{\theta }}_n\right]}^T$，同时设$g_{\theta }=\mathrm{diag}\left(\left[{\theta }_1,\cdots ,{\theta }_n\right]\right)$，就可以将上式的点积变成矩阵乘积：
$$x{\ast }_{G}y=U{g}_{\theta }{U}^{T}x$$

Spectral graph CNN

按照上面的卷积操作就可以按层设计谱域的卷积神经网络：
$${\mathbf{H}}_{:,j}^{(k)}=\sigma \left(\sum _{i=1}^{f_{k-1}}\mathbf{U}{\Theta }_{i,j}^{(k)}{\mathbf{U}}^T{\mathbf{H}}_{:,i}^{(k-1)}\right)\left(j=1,2,\cdots ,f_k\right)$$
卷积核就是${\mathbf{g}}_{\theta }={\Theta }_{i,j}^{(k)}$，这里的图信号就是多维度的，k是卷积层index，${\mathbf{H}}_{:,i}^{(k-1)}\in R^{n\times f_{k-1}}$是输入图信号（${\mathbf{H}}^{(0)}=\mathbf{X}$），$f_{k-1}$和$f_k$就是输入、输出通道数。但是矩阵的特征分解具有$O(n^3)$的复杂度，同时得到的U是稠密的，计算代价太高。

Chebyshev Spectral CNN (ChebNet)

通过多项式函数近似，参数化谱域卷积核：
$${\mathbf{g}}_{\theta }=\sum _{i=0}^K{\theta }_i{T}_i(\tilde{\mathbf{\Lambda }})$$

其中$\tilde{\Lambda }=2\mathbf{\Lambda }/{\lambda }_{\max }-I_n$，$\mathbf{\Lambda }\in [-1,1]$，这样的话参数的个数从n减少到了K，$T_i$通过切比雪夫多项式的递推公式得到：$T_i(x)=2x{T}_{i-1}(x)-T_{i-2}(x)$，$T_0(x)=1$，$T_1(x)=x$，那卷积公式变为
$$\mathbf{x}{\ast }_G{\mathbf{g}}_{\theta }=\mathbf{U}\left(\sum _{i=0}^K{\theta }_i{T}_i(\tilde{\mathbf{\Lambda }})\right){\mathbf{U}}^T\mathbf{x}$$

设$\tilde{\mathbf{L}}=2\mathbf{L}/{\lambda }_{\max }-{\mathbf{I}}_{\mathbf{n}}$，有$T_i(\tilde{\mathbf{L}})=\mathbf{U}{T}_i(\tilde{\mathbf{\Lambda }}){\mathbf{U}}^T$，ChebNet变成如下形式：
$$\mathbf{x}{\ast }_G{\mathbf{g}}_{\theta }=\sum _{i=0}^K{\theta }_i{T}_i(\tilde{\mathbf{L}})\mathbf{x}$$

ChebNet定义的滤波器在空间上是局域化的，这意味着滤波器可以独立于图的大小来提取局部特征；同时也不需要显式地求解U了。

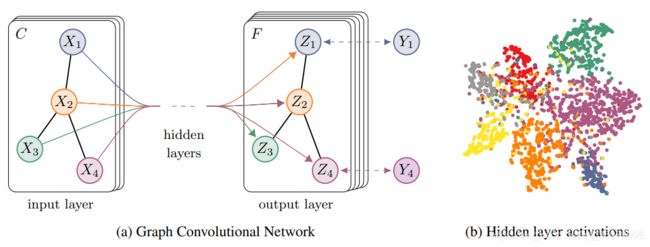
Graph Convolutional Network (GCN)

GCN是对ChebNet的一阶近似方法，假设上面的K=1且${\lambda }_{\max }=2$，那么$\mathbf{x}{\ast }_G{\mathbf{g}}_{\theta }={\sum }_{i=0}^K{\theta }_i{T}_i(\tilde{\mathbf{L}})\mathbf{x}$可以简化成
$$\mathbf{x}{\ast }_G{\mathbf{g}}_{\theta }={\theta }_0\mathbf{x}-{\theta }_1{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}\mathbf{x}$$

再假设两个$\theta$共享参数：${\theta }_0=-{\theta }_1=\theta$：
$$\mathbf{x}{\ast }_G{\mathbf{g}}_{\theta }=\theta \left({\mathbf{I}}_{\mathbf{n}}+{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}\right)\mathbf{x}=\theta \overline{\mathbf{A}}\mathbf{x}$$

再把单位阵和A合并起来得到$\overline{\mathbf{A}}={\tilde{\mathbf{D}}}^{-\frac{1}{2}}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-\frac{1}{2}}$，其中$\tilde{\mathbf{A}}=\mathbf{A}+{\mathbf{I}}_{\mathbf{n}}$，${\tilde{\mathbf{D}}}_{ii}={\sum }_j{\tilde{\mathbf{A}}}_{ij}$。这样就得到了GCN的卷积方法：
$$H^{l+1}=f(\overline{\mathbf{A}}{H}^l{W}^l)$$

$f$是激活函数。同时GCN也可以看做是一种空间方法，从一阶领域节点特征进行变换和聚合（究竟完成的是特征变换还是卷积操作不清楚了）。
提出GCN的文章里设计了两层的GCN网络用于半监督节点分类任务，有两个权重矩阵W，计算最后的交叉熵。
$$Z=f(X,A)=\mathrm{softmax}\left(\hat{A}\mathrm{ReLU}\left(\hat{A}X{W}^{(0)}\right)W^{(1)}\right)$$

空间方法

可以类比CNN的操作过程，直接在节点域定义卷积：选择节点的邻域、邻域节点排序、参数共享。

不像图像中卷积核滑动计算的过程，图中感受野的生成节点序列和感受野的形状完全由超参数决定。首先对每一个节点而言，选择固定数量的节点作为neighborhood（定义一种邻近度量方式），然后定序计算。

GraphSAGE

1. 随机采样邻域节点
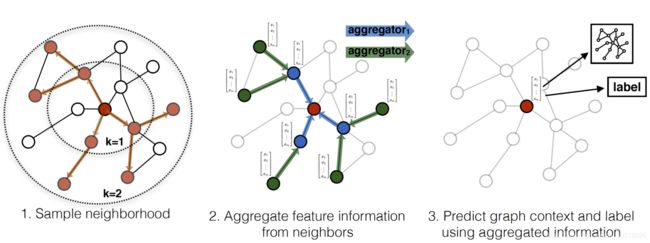
2. AGGREGATE+CONCAT(combine)
   

Graph Attention Network (GAT)

GCN还是利用了laplacian矩阵作为信息传递或者是聚合的工具，GAT采用注意机制来学习两个连接节点之间的相对权重，把卷积操作定义为
$${\mathbf{h}}_v^{(k)}=\sigma \left(\sum _{u\in \mathcal{N}(v)\cup v}{\alpha }_{vu}^{(k)}{\mathbf{W}}^{(k)}{\mathbf{h}}_u^{(k-1)}\right)$$

其中${\mathbf{h}}_v^{(0)}={\mathbf{x}}_v$，注意权$\alpha$度量两个相邻节点u之间的关联程度。
$${\alpha }_{ij}=\frac{\exp \left(\text{ LeakyReLU }\left({\mathbf{a}}^T\left[\mathbf{W}{h}_i\Vert \mathbf{W}{h}_j\right]\right)\right)}{{\sum }_{k\in {\mathcal{N}}_i}\exp \left(\text{ LeakyReLU }\left({\mathbf{a}}^T\left[\mathbf{W}{h}_i\Vert \mathbf{W}{h}_k\right]\right)\right)}$$

上式中除了特征变换参数W外还有一个参数a（权重向量），而在GCN中是由Laplacian矩阵硬性编码的。

Mixture Model Network (MoNet)

相比之下MoNet是更为一般的空间方法，定义图上的核函数，每一个核函数定义了一种度量任意两个节点相似度的方式，卷积就是对不同相似度定义的加权平均，卷积核的参数就是对应核函数的权重。在谱方法中，核函数就对应于谱变换的基，空间方法就是邻域节点的选择。
$$(f\star g)(x)=\sum _{j=1}^J{g}_j{D}_j(x)f$$

$g_j$就是卷积核参数，上面包含了一个patch operator $D_j(x)f$：
$$D_j(x)f=\sum _{y\in \mathcal{N}(x)}{w}_j(\mathbf{u}(x,y))f(y),j=1,\dots ,J$$

$u(x,y)$表示关系度量（没看懂文章这部分的表述），还有加权函数（kernel): ${\mathbf{w}}_{\Theta }(\mathbf{u})=\left(w_1(\mathbf{u}),\dots ,w_J(\mathbf{u})\right)$，$\Theta$是可学习参数。

tips

记一下有意思的结论：谱方法显式地定义了卷积核，而空间方法不需要；比如谱方法可以将特征投影到拉普拉斯矩阵特征向量定义的空间中，空间方法只需要kernel functions。
信号x关于graph的平滑程度可以刻画为（拉普拉斯矩阵L)：
$$x^{T}Lx=\sum _{(u,v)\in E}{A}_{uv}{\left(\frac{x_u}{\sqrt{d_u}}-\frac{x_v}{\sqrt{d_v}}\right)}^2$$

${\lambda }_i=u_i^{T}L{u}_i$可以视作$u_i$的频率，特征值刻画了特征向量关于图的平滑程度。$u_i{u}_i^T(1\le i\le n)$构成了一组基本滤波器，允许频率为${\lambda }_i$的信号通过，图上的谱卷积实际上是这组基本滤波器的线性组合：
$${\theta }_1{u}_1{u}_1^T+{\theta }_2{u}_2{u}_2^T+\cdots +{\theta }_n{u}_n{u}_n^T$$

ChebNet实际上是带了一组系数，频率越高系数越大（加强了高频信号，不体现平滑性，高通滤波器），对应的GCN就是一个类低通滤波。空间方法的重点是邻域节点选择的问题。
可惜的是网络学习的是节点信息的特征，而没有图结构特征；结构特征作为了信息传递和聚合的工具，即上下文学习。

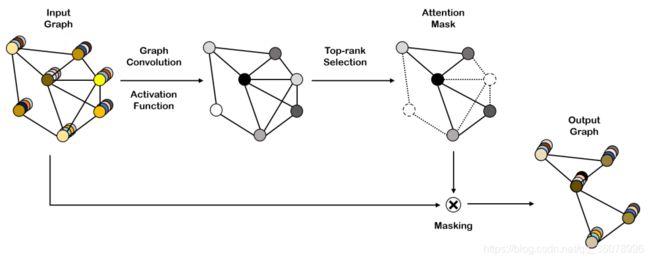
graph pooling

graph coarsening

其实是下采样过程，对节点进行聚类然后选取那些clusters作为新的节点(super node)。

node selection

首先学习一种对节点重要性的度量方法，然后根据这种度量选择一些重要的节点。