LeetCode 1361. 验证二叉树

二叉树上有 n 个节点，按从 0 到 n - 1 编号，其中节点 i 的两个子节点分别是 leftChild[i] 和 rightChild[i]。

只有 所有 节点能够形成且 只 形成 一颗 有效的二叉树时，返回 true；否则返回 false。

如果节点 i 没有左子节点，那么 leftChild[i] 就等于 -1。右子节点也符合该规则。

注意：节点没有值，本问题中仅仅使用节点编号。

示例 1：

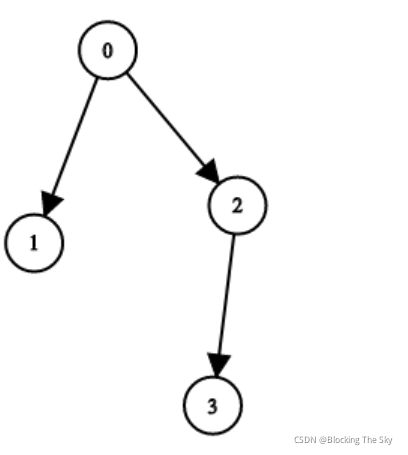
输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出：true

示例 2：

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
输出：false

DFS:

class Solution {
public:
    bool dfs(int root,vector<int>& leftChild, vector<int>& rightChild,int visited[]){
        visited[root]=true;
        bool a=true;
        bool b=true;
        if(leftChild[root]!=-1){
            if(visited[leftChild[root]]==0){
                visited[leftChild[root]]++;
                a=dfs(leftChild[root],leftChild,rightChild,visited);
            }
            else{
                return false;
            }
        }
        if(rightChild[root]!=-1){
            if(visited[rightChild[root]]==0){
                visited[rightChild[root]]++;
                b=dfs(rightChild[root],leftChild,rightChild,visited);
            }
            else{
                return false;
            }
        }
        return a&&b;
    }
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        int indegree[n];//记录每一个结点的入度
        memset(indegree,0,sizeof(indegree));
        for(int i=0;i<n;i++){
            if(leftChild[i]!=-1){
                indegree[leftChild[i]]++;
            }
            if(rightChild[i]!=-1){
                indegree[rightChild[i]]++;
            }
        }
        int root;//以唯一一个入度为0的结点作为根结点进行DFS
        int zero_indegree=0;//入度为0的结点个数大于1或者为0返回false
        for(int i=0;i<n;i++){
            if(indegree[i]==0){
                zero_indegree++;
                root=i;//记录"根结点"位置
            }
        }
        if(zero_indegree==0||zero_indegree>1){
            return false;
        }
        //下面以root为根结点开始DFS
        int visited[n];//访问数组
        memset(visited,0,sizeof(visited));
        if(!dfs(root,leftChild,rightChild,visited)){
            return false;
        }
        //下面以遍历一遍访问数组的方式验证是否有结点未访问(连通分量大于1),是则返回false,反之返回true
        for(int i=0;i<n;i++){
            if(visited[i]==0){
                return false;
            }
        }
        return true;
    }
};

BFS:

class Solution {
public:
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        int indegree[n];//记录每一个结点的入度
        memset(indegree,0,sizeof(indegree));
        for(int i=0;i<n;i++){
            if(leftChild[i]!=-1){
                indegree[leftChild[i]]++;
            }
            if(rightChild[i]!=-1){
                indegree[rightChild[i]]++;
            }
        }
        int root;//以唯一一个入度为0的结点作为根结点进行BFS
        int zero_indegree=0;//入度为0的结点个数大于1或者为0返回false
        for(int i=0;i<n;i++){
            if(indegree[i]==0){
                zero_indegree++;
                root=i;//记录"根结点"位置
            }
        }
        if(zero_indegree==0||zero_indegree>1){
            return false;
        }
        //下面以root为根结点开始BFS
        int visited[n];//访问数组
        memset(visited,0,sizeof(visited));
        queue<int> q;
        visited[root]++;
        q.push(root);
        while(!q.empty()){
            int p;
            p=q.front();
            q.pop();
            if(leftChild[p]!=-1){
                if(visited[leftChild[p]]==0){
                    q.push(leftChild[p]);
                    visited[leftChild[p]]++;
                }
                else{
                    return false;//一个结点被访问到第二次直接返回false
                }
            }
            if(rightChild[p]!=-1){
                if(visited[rightChild[p]]==0){
                    q.push(rightChild[p]);
                    visited[rightChild[p]]++;
                }
                else{
                    return false;//同上
                }
            }
        }
        //下面以遍历一遍访问数组的方式验证是否有结点未访问(连通分量大于1),是则返回false,反之返回true
        for(int i=0;i<n;i++){
            if(visited[i]==0){
                return false;
            }
        }
        return true;
    }
};