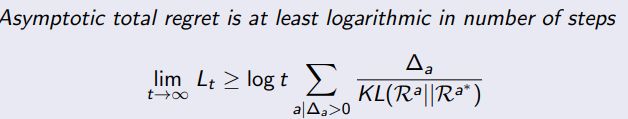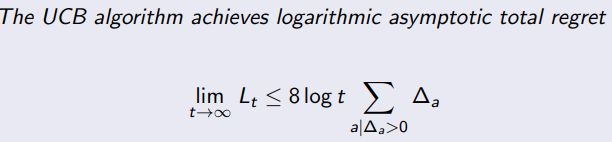David Silver Lecture 9:Exploration and Exploitation
1 Introduction
1.1 Outline
1.1.1 Exploration vs. Exploitation Dilemma
1.1.2 examples
1.1.3 principles
- Naive Exploration
在前面的章节主要使用的是naive exploration的方法 - Optimistic Initialisation
这种方法的思想是，我们对每个动作的奖励给出一个乐观的（即较高的）初始估计。这样，一开始，我们就会更倾向于探索，因为所有的动作都看起来很有吸引力。随着我们对每个动作的了解越来越深入，我们的估计会变得越来越准确，从而逐渐转向利用。
import numpy as np
class OptimisticInitialValueBandit:
def __init__(self, arm_count, initial_value):
self.arm_count = arm_count
self.values = np.full(arm_count, initial_value, dtype=float)
self.counts = np.zeros(arm_count, dtype=int)
def choose_arm(self):
return np.argmax(self.values)
def update(self, chosen_arm, reward):
self.counts[chosen_arm] += 1
self.values[chosen_arm] += (reward - self.values[chosen_arm]) / self.counts[chosen_arm]
def simulate():
bandit = OptimisticInitialValueBandit(2, 10.0) # We assume a very optimistic initial value
true_means = [0.5, 0.8]
for _ in range(1000):
arm = bandit.choose_arm()
reward = np.random.normal(true_means[arm], 1) # Assume the rewards are normally distributed
bandit.update(arm, reward)
simulate()
这个例子中的 values 变量代表的是对每个臂（行动）的预期奖励（expected reward）的估计，也就是强化学习中的动作值函数（action value function），或称为 Q-function。这个函数的作用是预测在给定状态下采取特定动作所能获得的预期奖励。
这个公式的作用是根据我们新的观测来更新我们对预期奖励的估计。reward - self.values[chosen_arm] 是观察到的奖励与当前估计的差异，称为预期奖励的误差（reward error）。然后我们将这个误差除以选择这个臂的次数，得到的结果是一个衡量误差的平均值。我们将这个平均误差添加到当前的估计上，从而对预期奖励的估计进行更新。
简单来说，这个公式的意义就是，每次当我们选择一个臂并观察到奖励后，我们就更新我们对这个臂的预期奖励的估计，使其更接近我们实际观察到的奖励。
- Optimism in the face of uncertainty
Optimism in the face of uncertainty 是一种在强化学习中处理探索与利用问题的策略。这种策略的基本理念是，当你对某个行为的结果不太确定时，要对其保持乐观。也就是说，你应该把不确定性视为潜在的机会，而不是风险。这样，你就更有可能去尝试那些你还不了解的行为，从而在长期中找到最好的策略。
下面是一个 Python 代码示例，使用 Optimism in the face of uncertainty 的方法来解决多臂赌博机问题。这个示例中，我们使用了一个简单的 Upper Confidence Bound (UCB) 算法：
import numpy as np
class UCBBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.counts = np.zeros(arm_count, dtype=int)
self.values = np.zeros(arm_count, dtype=float)
def choose_arm(self):
if 0 in self.counts: # If there's an arm we haven't tried, try it
return np.argmin(self.counts)
else: # Otherwise, be optimistic in the face of uncertainty
ucb_values = self.values + np.sqrt(2 * np.log(sum(self.counts)) / self.counts)
return np.argmax(ucb_values)
def update(self, chosen_arm, reward):
self.counts[chosen_arm] += 1
self.values[chosen_arm] += (reward - self.values[chosen_arm]) / self.counts[chosen_arm]
def simulate():
bandit = UCBBandit(2)
true_means = [0.5, 0.8]
for _ in range(1000):
arm = bandit.choose_arm()
reward = np.random.normal(true_means[arm], 1) # Assume the rewards are normally distributed
bandit.update(arm, reward)
simulate()
ucb_values = self.values + np.sqrt(2 * np.log(sum(self.counts)) / self.counts)
UCB 算法的全名是 Upper Confidence Bound 算法，它的核心思想是采取那些可能使得总收益最大的动作。在实际应用中，为了进行探索，我们常常不仅考虑那些平均回报高的动作，而且也考虑那些尝试次数少、不确定性高的动作。UCB 的基本形式如下：
在这里， Q ( a ) Q(a) Q(a) 是我们对动作 a a a 的预期收益的估计， N ( a ) N(a) N(a) 是我们尝试动作 a a a 的次数， N N N 是总的尝试次数。这个公式的第一部分 Q ( a ) Q(a) Q(a) 代表我们对动作 a a a 的预期收益的估计，这对应于 exploitation；而第二部分 2 ln N N ( a ) \sqrt{\frac{2 \ln N}{N(a)}} N(a)2lnN 是对我们对动作 a a a 的不确定性的估计，这对应于 exploration。乘数 2 是用来调整 exploration 和 exploitation 之间的平衡的，常常是经验选择的。对数函数 ln N \ln N lnN 是为了保证随着尝试次数的增加，对不确定性的估计会逐渐变小。
在上述 Python 代码中的 ucb_values = self.values + np.sqrt(2 * np.log(sum(self.counts)) / self.counts) 就是按照这个公式来计算每个动作的 UCB 值的。其中，self.values 对应于 Q ( a ) Q(a) Q(a)，sum(self.counts) 对应于 N N N，self.counts 对应于 N ( a ) N(a) N(a)。
- Probability Matching
Probability Matching 是一种常用于解决多臂赌博机问题的策略。根据这种策略，行动的选择概率与其被认为是最优行动的概率匹配。换言之，如果一个行动被认为是最优行动的概率是 p，那么这个行动被选择的概率也是 p。
这种策略的一个常见实现方法是 Thompson Sampling，也称为后验概率抽样。Thompson Sampling 是一种贝叶斯方法，根据我们对每个行动的后验概率来进行抽样，然后选择抽样结果最大的行动。
以下是一个简单的 Thompson Sampling 的 Python 代码示例，用于解决二元赌博机问题：
import numpy as np
from scipy.stats import beta
class ThompsonSamplingBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.successes = np.zeros(arm_count, dtype=int)
self.failures = np.zeros(arm_count, dtype=int)
def choose_arm(self):
samples = [beta(self.successes[i] + 1, self.failures[i] + 1).rvs() for i in range(self.arm_count)]
return np.argmax(samples)
def update(self, chosen_arm, reward):
if reward == 1:
self.successes[chosen_arm] += 1
else:
self.failures[chosen_arm] += 1
def simulate():
bandit = ThompsonSamplingBandit(2)
true_probs = [0.5, 0.8]
for _ in range(1000):
arm = bandit.choose_arm()
reward = np.random.binomial(1, true_probs[arm]) # Assume the rewards are binary
bandit.update(arm, reward)
simulate()
贝塔分布（Beta Distribution）是一种连续概率分布，它在 [0, 1] 区间上定义，由两个参数 alpha 和 beta 控制其形状。贝塔分布通常用于描述成功概率或比率的随机变量的概率分布，比如抛硬币的正面概率。
贝塔分布的概率密度函数（PDF）如下：
f ( x ; α , β ) = x α − 1 ( 1 − x ) β − 1 B ( α , β ) f(x;\alpha, \beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)} f(x;α,β)=B(α,β)xα−1(1−x)β−1
其中， B ( α , β ) B(\alpha, \beta) B(α,β) 是 Beta 函数，用于归一化，使得分布的总概率为1。这个函数会随着 alpha 和 beta 的变化而变化，它的形状可以在一定范围内变化，可以是单峰的，也可以是双峰的，峰值可以在 0 或 1 附近，也可以在中间。
在强化学习中，贝塔分布被用于伯努利试验（Bernoulli trial）中的未知概率。因为贝塔分布是二项分布（Binomial distribution）和伯努利分布（Bernoulli distribution）的共轭先验，也就是说，如果你有一些成功和失败的数据，你可以通过更新贝塔分布的参数来更新你的信念。
from scipy.stats import beta
import matplotlib.pyplot as plt
import numpy as np
# 假设我们有一个赌博机臂，我们尝试了10次，成功了3次，失败了7次
successes = 3
failures = 7
# 这样我们就有了一个参数为 alpha=successes+1, beta=failures+1 的贝塔分布
alpha = successes + 1
beta_param = failures + 1
# 我们可以画出这个分布的形状
x = np.linspace(0, 1, 1000)
y = beta.pdf(x, alpha, beta_param)
plt.plot(x, y)
plt.title('Beta Distribution')
plt.xlabel('Success Probability')
plt.ylabel('Density')
plt.show()
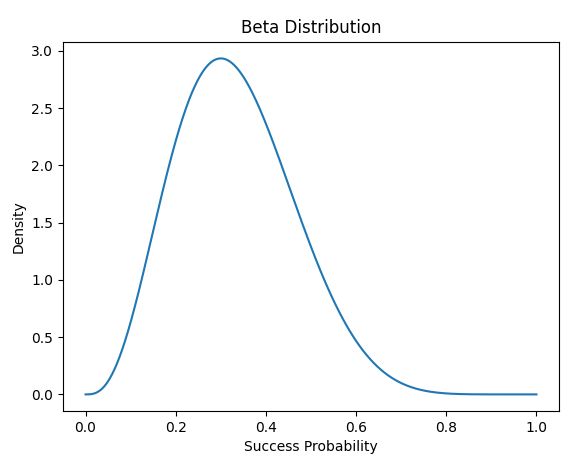
这个代码会画出一个贝塔分布的图像。你会看到，这个分布的峰值大约在 0.3 附近，这正好是我们观察到的成功概率（3/10）。同时，这个分布的宽度反映了我们对这个成功概率的不确定性：尝试次数越多，我们对成功概率的了解就越准确，不确定性就越小，分布就越窄；尝试次数越少，我们对成功概率的了解就越不准确，不确定性就越大，分布就越宽。
- information state search
信息状态搜索（Information State Search）是强化学习中的一种概念，它是为了解决部分可观察马尔科夫决策过程（POMDP）问题。在POMDP中，Agent不能完全观察到环境的状态，这就导致了环境状态与Agent的信念状态之间的区别。信息状态，也称为信念状态，表示的是在给定过去观察和行动的情况下，对环境状态的所有可能性的概率分布。
一个简单的例子就是扑克游戏。在扑克游戏中，你不能观察到对手的牌，所以你不能确定游戏的真实状态。但是你可以根据你的牌，对手的行动，以及一些统计信息（例如对手的平均下注量）来形成一个信念状态，即你认为游戏状态可能是什么。然后你就可以根据这个信念状态来决定你的行动。
在POMDP中进行信息状态搜索通常需要复杂的算法，如蒙特卡罗搜索树（MCTS），其中每个节点表示一个信息状态，而边表示从一个信息状态到另一个信息状态的行动。由于这需要大量的计算，所以通常会结合函数逼近方法（如深度学习）来进行。
下面的 Python 代码展示了一个简单的信息状态搜索的例子。在这个例子中，我们假设有一个非确定性的环境，Agent可以采取行动0或1，但是它不能直接观察到环境状态，只能观察到一个模糊的信号。然后我们用一个简单的策略，即如果信号大于0.5就采取行动0，否则采取行动1。
import numpy as np
class Environment:
def __init__(self):
self.state = np.random.rand()
def step(self, action):
if action == (self.state > 0.5):
reward = 1
else:
reward = 0
self.state = np.random.rand()
signal = self.state + np.random.normal(0, 0.1)
return signal, reward
class Agent:
def __init__(self):
self.belief_state = np.random.rand()
def update_belief_state(self, signal):
self.belief_state = signal
def choose_action(self):
if self.belief_state > 0.5:
return 0
else:
return 1
def main():
env = Environment()
agent = Agent()
total_reward = 0
for _ in range(100):
action = agent.choose_action()
signal, reward = env.step(action)
agent.update_belief_state(signal)
total_reward += reward
print('Total reward:', total_reward)
main()
在这个例子中，Agent不能直接观察到环境状态，但是它可以通过观察到的信号来更新它的信念状态，然后根据信念状态来选择行动。虽然这个策略非常简单，但是它在某种程度上反映了信息状态搜索的思想。
2 Multi-Armed Bandits
2.1 outline
多臂赌博机（Multi-Armed Bandit）问题是一种简化的强化学习问题，其中只有一个状态。这个问题的名字来自赌场的老虎机：一台有许多拉杆的赌博机就像有许多手臂的强盗。
在这个问题中，代理需要在多个动作（或“手臂”）之间进行选择，每个动作都会给出不确定的奖励。目标是通过试验学习并找出哪个动作能够最大化总奖励。
多臂赌博机问题的一个关键挑战是权衡探索（exploration）和利用（exploitation）：即选择你目前认为最佳的动作（利用）还是试验一些你还不太确定的动作（探索）。
例如，假设你面前有三台老虎机，每台老虎机的奖励概率不同，你需要决定在每台机器上投入多少时间，以期望最大化收益。这就是一个典型的多臂赌博机问题。
下面是一个使用 ε-greedy 算法解决这个问题的 Python 代码示例：
import numpy as np
class MultiArmedBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.arm_values = np.random.normal(0, 1, arm_count)
self.est_values = np.zeros(arm_count)
self.tries = np.zeros(arm_count)
def get_reward(self, action):
return np.random.normal(self.arm_values[action], 1)
def choose_arm(self, epsilon):
if np.random.rand() > epsilon:
return np.argmax(self.est_values)
else:
return np.random.randint(self.arm_count)
def update_est_values(self, action, reward):
self.tries[action] += 1
self.est_values[action] += (reward - self.est_values[action]) / self.tries[action]
def simulate():
bandit = MultiArmedBandit(10)
epsilon = 0.1
for _ in range(1000):
arm = bandit.choose_arm(epsilon)
reward = bandit.get_reward(arm)
bandit.update_est_values(arm, reward)
print("Estimated arm values:", bandit.est_values)
simulate()
在这个代码中，MultiArmedBandit 类模拟了一个多臂赌博机，每个手臂的真实值都是从均值为 0、标准差为 1 的正态分布中随机生成的。然后我们进行 1000 次试验，每次试验中，我们使用 ε-greedy 算法选择一个手臂，并根据收到的奖励更新我们对该手臂值的估计。最后，我们输出了每个手臂的估计值。
2.2 Regret
- Regret
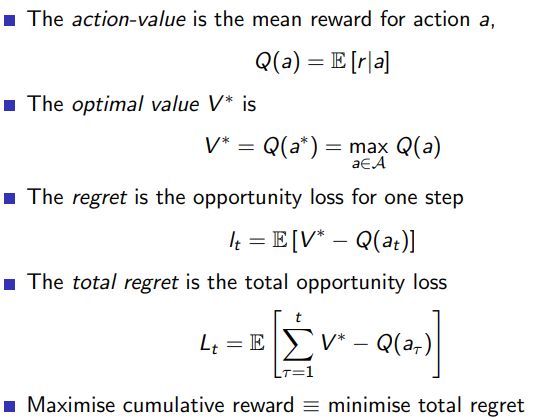
- Counting Regret
在强化学习中，regret（遗憾）是一个重要的概念，它衡量的是一个学习算法与理想策略的性能差距。更具体地说，遗憾是算法选择的动作产生的累积奖励与最优策略产生的最大可能累积奖励之间的差值。如果遗憾越大，那么算法的性能就越差；如果遗憾小，那么算法的性能就接近最优。
在多臂赌博机问题中，遗憾是一个特别重要的性能度量。例如，对于一个给定的赌博机，如果我们总是选择最优的手臂（即平均奖励最高的手臂），那么我们将获得最大可能的累积奖励。然而，如果我们以某种方式选择手臂，如 ε-greedy 算法，那么我们可能会选择到非最优的手臂，从而导致遗憾。
以下是一个计算多臂赌博机问题中遗憾的 Python 代码示例：
import numpy as np
class MultiArmedBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.arm_values = np.random.normal(0, 1, arm_count)
self.est_values = np.zeros(arm_count)
self.tries = np.zeros(arm_count)
def get_reward(self, action):
return np.random.normal(self.arm_values[action], 1)
def choose_arm(self, epsilon):
if np.random.rand() > epsilon:
return np.argmax(self.est_values)
else:
return np.random.randint(self.arm_count)
def update_est_values(self, action, reward):
self.tries[action] += 1
self.est_values[action] += (reward - self.est_values[action]) / self.tries[action]
def simulate():
bandit = MultiArmedBandit(10)
epsilon = 0.1
total_regret = 0
best_arm_value = np.max(bandit.arm_values)
for _ in range(1000):
arm = bandit.choose_arm(epsilon)
reward = bandit.get_reward(arm)
bandit.update_est_values(arm, reward)
total_regret += best_arm_value - reward
print("Total regret:", total_regret)
simulate()
2.3 Greedy and ϵ − \epsilon- ϵ−greedy algorithms
- greedy algorithm
- ϵ − \epsilon- ϵ−Greedy Algorithm
- Optimistic Initialisation
- Decayling ϵ t − \epsilon_t- ϵt−Greedy Algorithm
2.4 Lower Bound
- lower bound
Theorem (Lai and Robbins)
Lai and Robbins 在 1985 年提出了一个著名的理论结果，这个结果界定了解决多臂赌博机问题时任何策略的遗憾的下界。这个定理指出，在有限的多臂赌博机环境中，任何策略都无法保证其遗憾小于一个特定的值。因此，这个定理为评估和比较不同策略提供了一个基准。
这个定理的直觉含义是，要找出最好的手臂（即奖励最大的手臂），你必须至少试验一次每个手臂。在试验过程中，你可能会获得较小的奖励，这就产生了遗憾。因此，无论你使用什么策略，只要你试图找出最好的手臂，你都会有一些遗憾。
R ( T ) ≥ ∑ i : μ i < μ ∗ ( μ ∗ − μ i ) log ( T ) D ( μ i ∣ ∣ μ ∗ ) R(T) \geq \sum_{i: \mu_i < \mu^*} \frac{(\mu^* - \mu_i) \log(T)}{D(\mu_i || \mu^*)} R(T)≥i:μi<μ∗∑D(μi∣∣μ∗)(μ∗−μi)log(T)
其中，R(T) 是 T 轮后的遗憾，mu* 是最好手臂的平均奖励，mu_i 是第 i 个手臂的平均奖励，D(mu_i, mu*) 是两个伯努利分布之间的 Kullback-Leibler 散度。注意这个公式是针对二值奖励情况推导出来的，但在很多情况下也可以用来近似其他类型的奖励。
这个定理的应用范围主要是强化学习和在线学习中的多臂赌博机问题，例如广告展示、推荐系统、网络路由等问题，都可以形式化为多臂赌博机问题，这个定理为设计和评估这些问题的策略提供了理论基础。
2.5 Upper Confidence Bound
- Optimism in the Face of Uncertainty
2.6 Upper Confidence Bound
Upper Confidence Bounds (UCB) 是一种解决多臂赌博机问题的策略。它的核心思想是在选择行动时，同时考虑到了每个行动的平均回报和不确定性。
在多臂赌博机问题中，UCB 策略根据每个手臂的潜在价值来选择手臂。每个手臂的潜在价值是根据其平均回报以及被选中的次数来估计的。具体来说，如果一个手臂被选中的次数较少，那么我们对其真实回报的不确定性就越大，因此，它的潜在价值就越高。反之，如果一个手臂被选中的次数较多，那么我们对其真实回报的不确定性就越小，但是如果这个手臂的平均回报很高，那么它的潜在价值依然可能很高。
UCB 策略在每一步中都选择具有最高上界置信度的手臂，这种方法体现了对探索和利用的平衡。探索部分来自于被选中次数较少的手臂具有更高的不确定性，而利用部分则来自于选择平均回报较高的手臂。
UCB 策略的优点是它能够较好地权衡探索和利用，而且它具有理论上的遗憾界。在实际中，UCB 策略已经被成功应用于各种领域，如在线广告展示、推荐系统等。
-
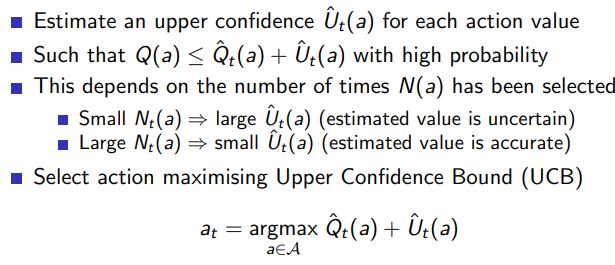
Hoeffding’s inequality
Hoeffding’s Inequality 是一种概率不等式，它为一组随机变量的平均值与其期望值之间的差值提供了一个上界。这个不等式是在一定的假设下得到的，主要是每个随机变量都是独立同分布的，并且都被限制在一个特定的范围内。
其中，
P ( ∣ 1 n ∑ i = 1 n ( X i − E [ X i ] ) ∣ ≥ t ) ≤ 2 exp ( − 2 n 2 t 2 B 2 ) P\left(\left|\frac{1}{n}\sum_{i=1}^{n}(X_{i} - E[X_{i}])\right| \geq t\right) \leq 2 \exp\left(-\frac{2n^2t^2}{B^2}\right) P( n1i=1∑n(Xi−E[Xi]) ≥t)≤2exp(−B22n2t2) -
P 是概率，
-
X_i 是第 i 个随机变量，
-
E[X_i] 是 X_i 的期望值，
-
n 是随机变量的数量，
-
t 是我们关心的阈值，
-
B 是随机变量可能取值的范围。
这个不等式的直觉含义是：如果我们有一组独立同分布的随机变量，并且这些变量的取值都被限制在一定的范围内，那么这些变量的平均值与期望值之间的差值大于某个阈值 t 的概率是非常小的，并且这个概率随着样本数量 n 的增加而指数级地下降。
Hoeffding’s Inequality 在许多统计和机器学习的问题中都有重要应用，例如在多臂赌博机问题中，它可以用来估计每个手臂的奖励的不确定性，以及在深度学习中，它被用于理解模型训练过程中的泛化误差等。
- Calculating upper confidence bounds
- UCB1
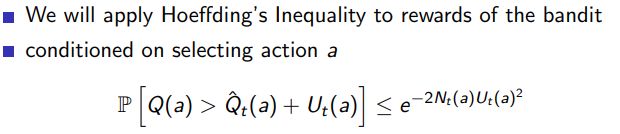
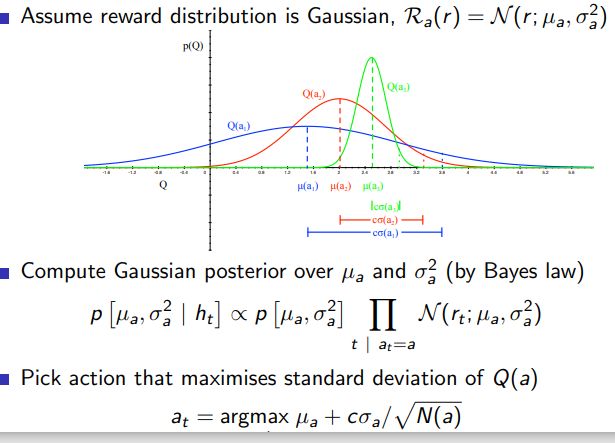
2.7 Bayesian Bandits
Bayesian Bandits 是多臂赌博机问题中的一种方法，它基于贝叶斯推理对每个行动的奖励分布进行更新。不同于其他策略（如 ε-greedy 或 UCB），贝叶斯方法在每次选择一个行动并观察到其奖励后，会更新我们对那个行动奖励的分布的认识。
在贝叶斯赌博机中，每个行动都有一个与之关联的概率分布。当我们选择一个行动并观察到结果时，我们会根据观察到的结果更新这个行动的分布。这通常通过应用贝叶斯定理来完成。
例如，假设我们有一个两臂赌博机，每个臂的奖励服从伯努利分布。我们先假设两个臂的奖励概率都是未知的，并分别服从均匀分布。然后我们可以采用贝叶斯赌博机策略来解决这个问题。
以下是一个 Python 代码示例：
import numpy as np
from scipy.stats import beta
class BayesianBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.alpha = np.ones(arm_count)
self.beta = np.ones(arm_count)
def choose_arm(self):
sample_means = [np.random.beta(self.alpha[i], self.beta[i]) for i in range(self.arm_count)]
return np.argmax(sample_means)
def update(self, chosen_arm, reward):
self.alpha[chosen_arm] += reward
self.beta[chosen_arm] += 1 - reward
def simulate():
bandit = BayesianBandit(2)
true_means = [0.5, 0.8]
for _ in range(1000):
arm = bandit.choose_arm()
reward = np.random.binomial(1, true_means[arm])
bandit.update(arm, reward)
simulate()
在这个代码中，我们创建了一个贝叶斯赌博机，它有两个臂，每个臂的奖励服从伯努利分布。我们采样每个臂的分布以选择一个臂，然后根据观察到的奖励更新选中的臂的分布。
- Thompson Sampling
Lai 和 Robbins 的定理表明在多臂赌博机问题中，任何算法的累计遗憾（cumulative regret）必须随着时间的推移线性增长。换句话说，没有任何算法能够做得比这个下界更好。这是因为如果要找到最优的臂，算法必须尝试所有的臂，这就导致了一定的遗憾。
Thompson Sampling 是一种解决多臂赌博机问题的贝叶斯算法。它不直接估计每个臂的平均奖励，而是维护每个臂奖励的概率分布，并在选择臂时进行随机抽样。它的主要优点是能够自然地平衡探索和利用。
有研究证明，Thompson Sampling 满足 Lai 和 Robbins 的下界，也就是说，它的累计遗憾随着时间的推移线性增长。这意味着它是一个渐进最优的算法，也就是说，当尝试次数趋于无穷大时，它的遗憾增长速率可以达到最优。
需要注意的是，尽管 Thompson Sampling 满足 Lai 和 Robbins 的下界，但这并不意味着在所有情况下，Thompson Sampling 都是最优的算法。在实际问题中，哪种算法最优往往取决于问题的具体情况。
2.6 Information state search
- Value of information
- Information State Space
- example: Bernoulli Bandits
Bernoulli Bandit 是一种特殊类型的多臂赌博机问题，每个臂的奖励分布都是伯努利分布。伯努利分布是一个二值随机变量分布，它的值只有两种可能结果，例如1（成功）和0（失败）。在 Bernoulli Bandit 中，每个臂被拉动时，成功的概率（例如得到奖励1）是固定的，但是这个概率值通常是未知的，需要通过多次尝试去估计。
Bernoulli Bandit 的一个常见应用场景是在线广告投放。假设我们有多种广告可供选择，每次用户点击某种广告，我们就获得了奖励（例如设置为1）。否则，没有奖励（设置为0）。我们的目标是找出最具吸引力（即点击概率最高）的广告。
下面是使用 Thompson Sampling 算法解决 Bernoulli Bandit 问题的
import numpy as np
from scipy.stats import beta
class BernoulliBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.alpha = np.ones(arm_count)
self.beta = np.ones(arm_count)
def choose_arm(self):
sample_means = [np.random.beta(self.alpha[i], self.beta[i]) for i in range(self.arm_count)]
return np.argmax(sample_means)
def update(self, chosen_arm, reward):
self.alpha[chosen_arm] += reward
self.beta[chosen_arm] += 1 - reward
def simulate():
bandit = BernoulliBandit(2)
true_probs = [0.5, 0.8]
for _ in range(1000):
arm = bandit.choose_arm()
reward = np.random.binomial(1, true_probs[arm])
bandit.update(arm, reward)
simulate()
初始化了一个具有两个臂的 Bernoulli Bandit，其中每个臂的奖励都服从伯努利分布。然后我们使用 Thompson Sampling 算法在每一步中选择一个臂，并根据实际的奖励更新我们对每个臂奖励分布的估计。这个过程持续1000步，最后我们可以得到每个臂的奖励分布的估计。
- solving information state space bandits
- Bayes-Adaptive Bernoulli Bandits
Bayes-Adaptive Bernoulli Bandits 是一种在 Bernoulli Bandits 框架下的贝叶斯自适应方法。这种方法考虑了每个臂的奖励分布可能随时间而改变，并利用贝叶斯更新来适应这种改变。与固定臂的 Bernoulli Bandits 不同，Bayes-Adaptive 方法可以更好地处理动态环境。
每次选择一个臂并观察到奖励后，Bayes-Adaptive 方法会使用贝叶斯规则来更新我们对该臂的奖励分布的信念。具体来说，我们开始时对每个臂的奖励分布都有一个先验分布，然后根据观察到的奖励来更新这个分布。这个过程可以反复进行，从而使我们的信念随着时间的推移而自适应地更新。
下面是一个 Python 代码示例，这个示例中，我们假设每个臂的奖励分布都是伯努利分布，并且这个分布可能随时间而改变：
import numpy as np
from scipy.stats import beta
class BayesAdaptiveBernoulliBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.alpha = np.ones(arm_count)
self.beta = np.ones(arm_count)
def choose_arm(self):
sample_means = [np.random.beta(self.alpha[i], self.beta[i]) for i in range(self.arm_count)]
return np.argmax(sample_means)
def update(self, chosen_arm, reward):
self.alpha[chosen_arm] += reward
self.beta[chosen_arm] += 1 - reward
def simulate():
bandit = BayesAdaptiveBernoulliBandit(2)
true_probs = [0.5, 0.8]
for i in range(1000):
# Assume that the true probabilities change over time
true_probs = [0.5 + 0.3 * np.sin(i / 100), 0.8 - 0.3 * np.sin(i / 100)]
arm = bandit.choose_arm()
reward = np.random.binomial(1, true_probs[arm])
bandit.update(arm, reward)
simulate()
在这个代码中，我们首先初始化了一个具有两个臂的 Bayes-Adaptive Bernoulli Bandit。然后我们假设每个臂的奖励分布的真实概率会随着时间的推移而改变。在每一步中，我们选择一个臂，并根据观察到的奖励更新我们对该臂奖励分布的信念。这个过程持续1000步，最后我们可以得到每个臂的奖励分布的估计。
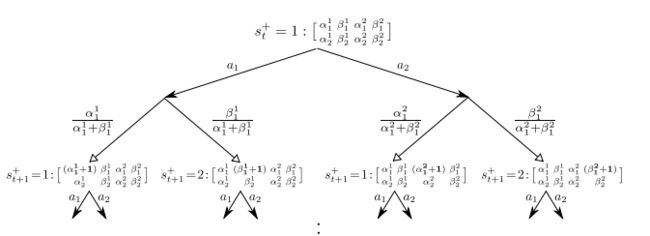
- Gittins indices for bernoulli Bandits
Gittins Index 是一种用于解决多臂赌博机问题的指数，它可以用于确定应选择哪个行动或臂。在贝叶斯环境中，每个臂的 Gittins Index 是根据该臂的预期奖励和不确定性计算出的。
Gittins Index 的一个关键特性是，它具有所谓的"分离性"。这意味着每个臂的 Index 只依赖于该臂自身的历史信息，而与其他臂的情况无关。因此，每次都可以选择具有最大 Gittins Index 的臂，而不用考虑其他臂的状态。
以下是一个 Gittins Index 的计算示例。这个例子中，我们假设每个臂的奖励服从伯努利分布，且已知每个臂的成功次数和总试验次数。由于 Gittins Index 的计算需要解决一个具有挑战性的优化问题，因此这里我们采用了一种简化的估计方法：
import numpy as np
class GittinsBernoulliBandit:
def __init__(self, arm_count):
self.arm_count = arm_count
self.successes = np.zeros(arm_count)
self.failures = np.zeros(arm_count)
def choose_arm(self):
estimated_gittins_indices = [self.successes[i] / (self.successes[i] + self.failures[i]) +
np.sqrt(2 * np.log(sum(self.successes) + sum(self.failures)) /
(self.successes[i] + self.failures[i]))
for i in range(self.arm_count)]
return np.argmax(estimated_gittins_indices)
def update(self, chosen_arm, reward):
if reward == 1:
self.successes[chosen_arm] += 1
else:
self.failures[chosen_arm] += 1
def simulate():
bandit = GittinsBernoulliBandit(2)
true_probs = [0.5, 0.8]
for _ in range(1000):
arm = bandit.choose_arm()
reward = np.random.binomial(1, true_probs[arm])
bandit.update(arm, reward)
simulate()
在这个代码中，我们首先初始化了一个具有两个臂的 Gittins Bernoulli Bandit。然后我们选择 Gittins Index 最大的臂，并根据观察到的奖励更新成功次数和失败次数。这个过程持续1000步，最后我们可以得到每个臂的成功次数和失败次数。
3 Contextual Bandits
3.1 outline
- Contextual Bandits
Contextual Bandits 是一种更为复杂的多臂赌博机问题，它在每一步中引入了上下文（context）。每当需要做决策时，都会有一个相关的上下文向量提供信息。与普通的多臂赌博机问题相比，Contextual Bandits 的主要区别是，它不仅要考虑选择哪个臂，而且还要考虑当前的上下文。
Contextual Bandits 的一个常见应用是个性化推荐。例如，当我们想向用户推荐文章时，上下文可能包括用户的个人信息、浏览历史等，我们的任务是根据这些上下文信息选择一个最可能让用户感兴趣的文章。
下面是一个简单的 Python 代码示例，使用线性回归模型来解决 Contextual Bandits 问题：
import numpy as np
from sklearn.linear_model import LinearRegression
class ContextualBandit:
def __init__(self, arm_count, context_dim):
self.arm_count = arm_count
self.context_dim = context_dim
self.models = [LinearRegression() for _ in range(arm_count)]
self.data = [np.zeros((0, context_dim)) for _ in range(arm_count)]
self.targets = [[] for _ in range(arm_count)]
def choose_arm(self, context):
predictions = [self.models[i].predict(context.reshape(1, -1)) if len(self.targets[i]) > 0 else 0
for i in range(self.arm_count)]
return np.argmax(predictions)
def update(self, chosen_arm, context, reward):
self.data[chosen_arm] = np.vstack([self.data[chosen_arm], context])
self.targets[chosen_arm].append(reward)
self.models[chosen_arm].fit(self.data[chosen_arm], self.targets[chosen_arm])
def simulate():
bandit = ContextualBandit(2, 3)
true_weights = [np.array([0.5, 0.3, 0.2]), np.array([0.2, 0.4, 0.4])]
for _ in range(1000):
context = np.random.uniform(-1, 1, 3)
arm = bandit.choose_arm(context)
reward = context.dot(true_weights[arm]) + 0.1 * np.random.randn()
bandit.update(arm, context, reward)
simulate()
在这个代码中，我们首先初始化了一个具有两个臂、每个臂都有一个线性回归模型的 Contextual Bandit。然后我们随机生成一个上下文，并选择预期奖励最大的臂。然后，我们根据真实的奖励更新所选臂的模型。这个过程持续1000步，最后我们可以得到每个臂的线性回归模型。
3.2 Linear UCB
3.2.1 Linear Regression
- Action-value function is expected reward for state s and action a
Q ( s , a ) = E [ r ∣ s , a ] Q(s,a)=E[r|s,a] Q(s,a)=E[r∣s,a] - Estimate value function with a linear function approximator
Q θ ( s , a ) = θ ( s , a ) T θ Q_{\theta}(s,a)=\theta(s,a)^T\theta Qθ(s,a)=θ(s,a)Tθ - Estimate parameters by least squares regression
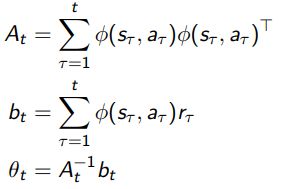
- Linear Upper Confidence bounds
3.2.2 Geometric Interpretation
3.2.3 Calculating linear Upper Confidence Bounds
4 MDPs
4.1 outline
4.2 optimistic Initialisation
4.2.1 Model-Free RL
4.2.2 Model Based RL
4.3 Optimism in the face of uncertainty
4.3.1 Bayesian Model based RL
4.4 Probability Matching
4.4.1 Thompson Sampling: model based RL
4.4.2 Information State Search
4.4.3 Bayes Adaptive MDPs
4.4.4 总结
