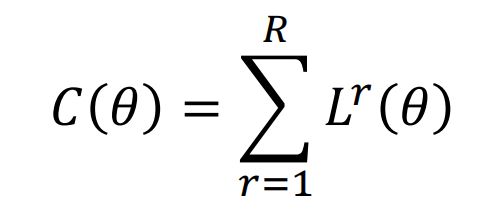【人工智能】— 神经网络、M-P 神经元模型、激活函数、神经网络结构、学习网络参数、代价定义、总代价

神经网络的历史

第一阶段
⚫ 1943年, McCulloch和Pitts 提出第一个神经元数学模型, 即M-P模型, 并从原理上证明了人工神经网络能够计算任何算数和逻辑函数
⚫ 1958年, Rosenblatt 提出感知机网络（Perceptron）模型和其学习规则
⚫ 1969年, Minsky和Papert 发表《Perceptrons》一书, 指出单层神经网路不能解决非线性问题, 多层网络的训练算法尚无希望. 这个论断导致神经网络进入低谷

第二阶段
⚫ 1986年, Rumelhart 等编辑的著作《Parallel Distributed Processing: Explorations in the Microstructures of Cognition》报告了反向传播算法
⚫ 1987年, IEEE 在美国加州圣地亚哥召开第一届神经网络国际会议（ICNN）
⚫ 90年代初, 伴随统计学习理论和SVM的兴起, 神经网络由于理论不够清楚, 试错性强, 难以训练, 再次进入低谷

第三阶段
⚫ 2006年, Hinton提出了深度信念网络(DBN), 通过“预训练+微调”使得深度模型的最优化变得相对容易
⚫ 2012年, Hinton 组参加ImageNet 竞赛, 使用 CNN 模型以超过第二名10个百分点的成绩夺得当年竞赛的冠军
⚫ 伴随云计算、大数据时代的到来，计算能力的大幅提升，使得深度学习模型在计算机视觉、自然语言处理、语音识别等众多领域都取得了较大的成功
⚫ 2018年图灵奖-Hinton, Bengio, LeCun

Neural Network Intro

“神经网络是由具有适应性的简单单元组成的广泛并行互联的网络, 它的组织能够模拟生物神经系统对真实世界物体所作出的反应”
⚫ 机器学习中的神经网络通常是指“神经网络学习” 或者机器学习与神经网络两个学科的交叉部分
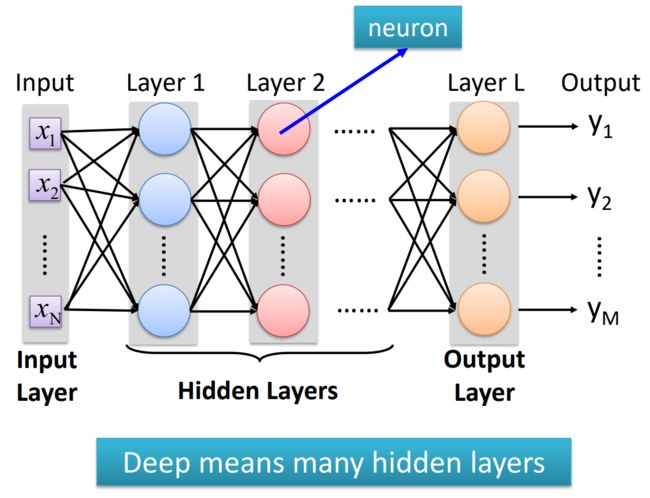
⚫ 神经元模型即上述定义中的“简单单元”是神经网络的基本成分
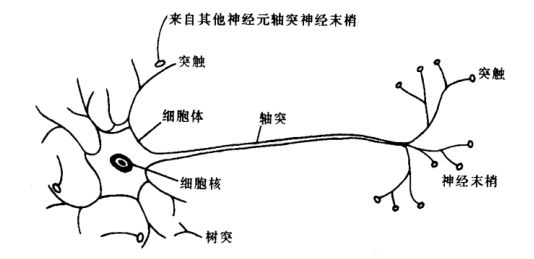
⚫ 生物神经网络：每个神经元与其他神经元相连, 当它“兴奋”时, 就会向相连的神经云发送化学物质, 从而改变这些神经元内的电位；如果某神经元的电位超过一个“阈值”, 那么它就会被激活, 即“兴奋”起来, 向其它神经元发送化学物质

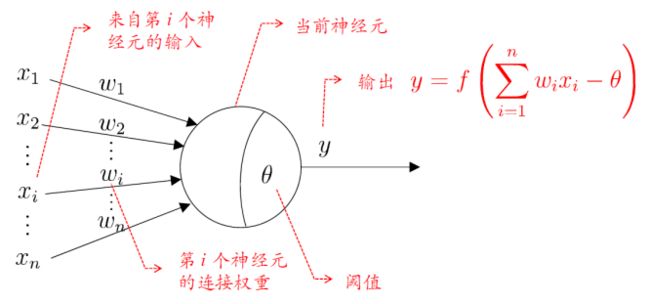
M-P 神经元模型

⚫ 输入：来自其它n个神经元传递过来的输入信号
⚫ 处理：输入信号通过带权重的连接进行传递, 神经元接受到总输入值将与神经元的阈值进行比较
⚫ 输出：通过激活函数的处理以得到输出

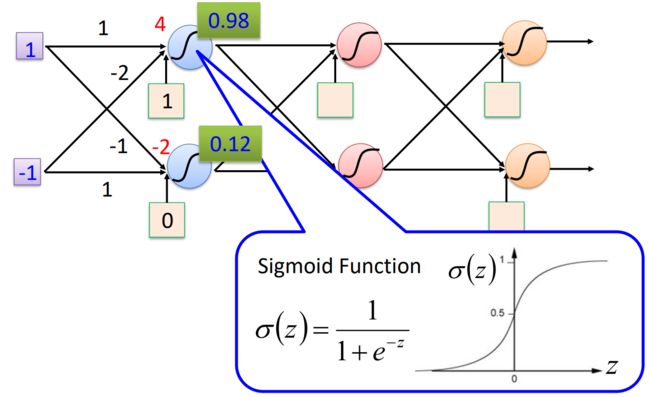
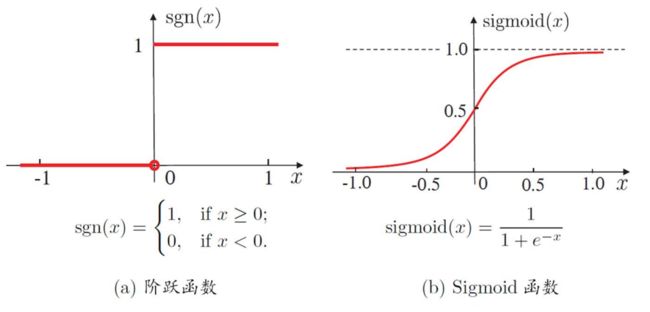
激活函数(Activation function)

⚫ 理想激活函数是阶跃函数, 0表示抑制神经元而1表示激活神经元
⚫ 阶跃函数具有不连续、不光滑等不好的性质, 常用的是 Sigmoid 函数

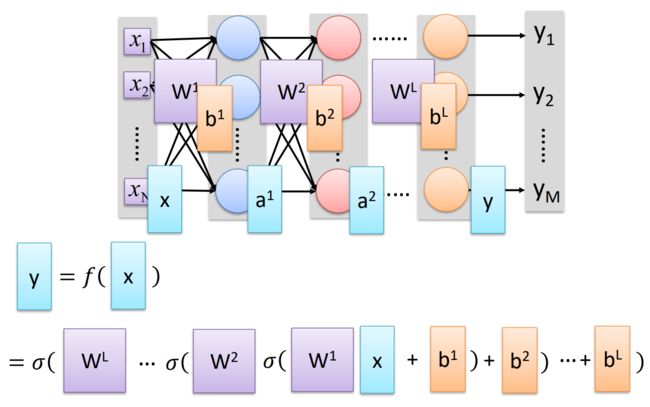
神经网络结构

举例

训练神经网络

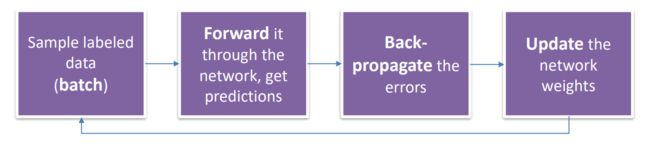
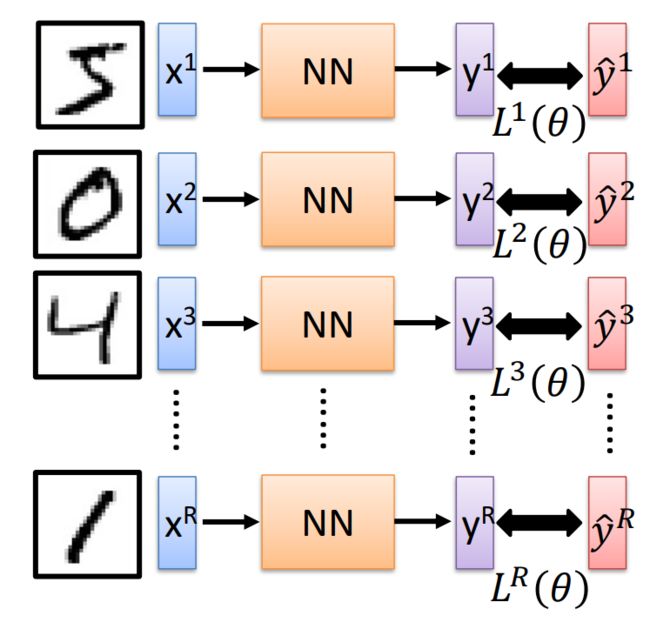
学习网络参数

1. 使用标记的样本数据（批量）
2. 将其输入神经网络，获取预测结果
3. 反向传播误差
4. 更新神经网络的权重

这是神经网络训练的基本步骤。首先，将一批标记的样本数据输入到神经网络中，通过前向传播计算得到预测结果。然后，通过与真实标签进行比较，计算出预测结果与真实结果之间的误差。接下来，使用反向传播算法将误差从输出层向后传播，逐层计算并更新每个神经元的梯度和权重。最后，根据更新后的权重继续进行下一轮的训练，不断迭代优化神经网络的性能，直到达到预定的停止条件。

代价定义

成本函数（Cost）的定义可以是网络输出与目标之间的欧氏距离或交叉熵。

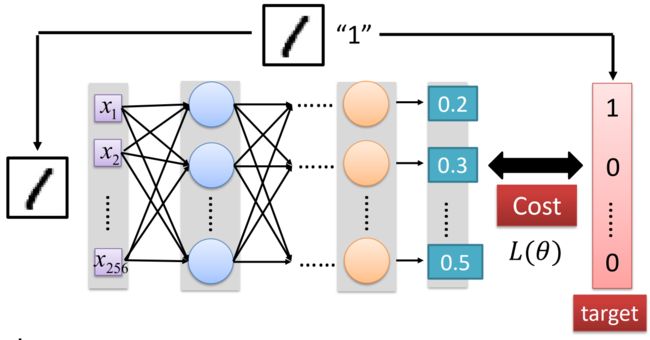
在神经网络训练中，成本函数用于衡量神经网络的预测结果与真实标签之间的差异。成本函数的选择取决于具体的任务和网络结构。

均方误差

欧氏距离也称为均方误差（Mean Squared Error，MSE）。它计算预测结果与真实标签之间的差的平方的平均值。

交叉熵（Cross Entropy）

交叉熵特别适用于分类问题。对于每个样本，成本函数的计算公式为：

$$Cost=-(1/N)\ast \Sigma (y_{true}\ast \log (y_{pred})+(1-y_{true})\ast \log (1-y_{pred}))$$

其中，N是样本数量，y_pred是神经网络的预测结果（经过激活函数处理），y_true是真实标签。

总代价

总成本（Total Cost）衡量了神经网络参数 在该任务上的拟合程度或性能表现的好坏。

在神经网络训练中，我们通过最小化总成本来寻找最优的参数 。