C++题解:树的直径
题目描述
树中两点间的不重复经过的边和点道路称为两点的路径,路径的长度(路径上所经边的长度和)称为两点的距离。圆的直径是一个圆的最长的一条弦,而树的直径是树中两点间最长的路径。通常用一个无序点对(x,y)表示一棵树的直径。
现在输入一个有n个结点的树,结点编号为1到n,假设结点1为根。试求树的直径。
输入格式
输入包含n+1行,第一行为1个正整数n,表示树的结点个数。
接下来n-1行,每行两个整数x和y,表示结点x和y之间有一条边,其中x是y的父亲。
输出格式
输出只有一个整数,为树的直径。
数据范围
n ≤ 1 0 5 n≤10^5 n≤105
输入样例
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例
22
算法思想
在树中任取一个结点 t t t,求到 t t t距离最远的结点 u u u,接着求到 u u u距离最远的结点 v v v,那么结点 u u u和 v v v之间的路径就是树的一条直径。
证明
根据上述思想,只需证明第一次找到的结点 u u u一定是某条直径的端点即可。
反证法:假设距离 t t t最远的结点 u u u不是某条直径的端点,并且存在某条直径,其端点分别为 x x x、 y y y。那么 t t t到 u u u之间的路径和 x x x到 y y y 之间的路径,根据有无公共结点,可分为相交和不相交两种情况,如下图所示:
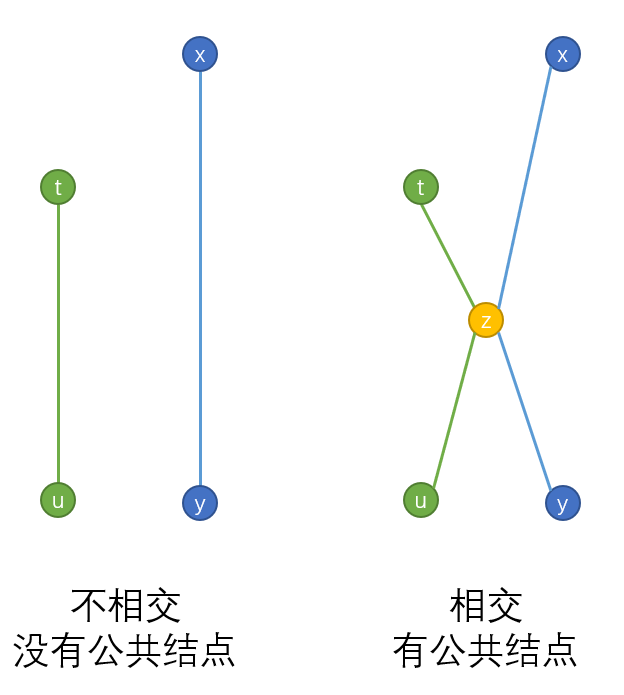
- 不相交的情况
因为树是连通的,所以从结点 t t t一定存在一条路径能够到达结点 y y y,如下图所示:
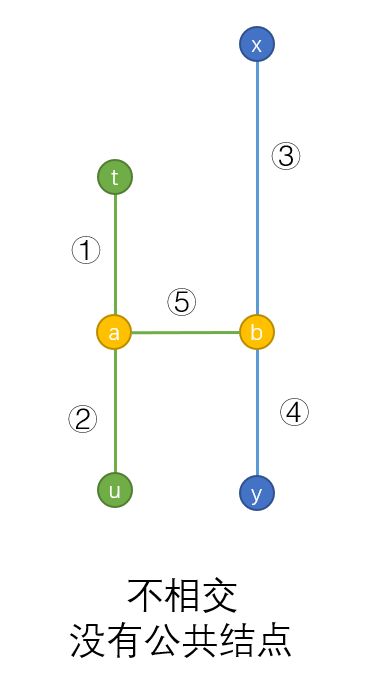
由于 u u u是到 t t t距离最远的点,所以 ① + ② ≥ ① + ⑤ + ④ ①+②\ge①+⑤+④ ①+②≥①+⑤+④,那么 ② ≥ ⑤ + ④ ②\ge⑤+④ ②≥⑤+④, ② + ⑤ ≥ ④ ②+⑤\ge④ ②+⑤≥④。我们假设 x y xy xy是树的一条直径,即 ③ + ④ ③+④ ③+④一定是树中最长的路径,而 ② + ⑤ + ③ ≥ ③ + ④ ②+⑤+③\ge③+④ ②+⑤+③≥③+④,所以如结点 u u u不是某条直径的端点,那么树中一定存在一条大于等于当前直径的路径,与假设矛盾。
- 相交的情况

由于 u u u是到 t t t距离最远的点,所以 ① + ② ≥ ① + ④ ①+②\ge①+④ ①+②≥①+④,即 ② ≥ ④ ②\ge④ ②≥④,那么 ③ + ② ≥ ③ + ④ ③+②\ge③+④ ③+②≥③+④。我们假设 x y xy xy是树的一条直径,即 ③ + ④ ③+④ ③+④一定是树中最长的路径,如果结点 u u u不是某条直径的端点,那么树中一定存在一条大于等于当前直径的路径,与假设矛盾。
证毕。
算法实现
使用邻接表实现一棵无根树,在树中任取一个结点t:
- 通过DFS求出所有点
i到t的距离dep[i] - 打擂台,求出到
t距离最远的结点u - 使用相同的方法求出到
u距离最远的结点v dep[v]就是树的直径
时间复杂度
需要对所有节点遍历一次,时间复杂度为 O ( n ) O(n) O(n)
代码实现一(简单模拟)
#include 代码实现二(求最长、次长深度)
#include