图的操作算法详解
一.图
基础概念:
- 有向图 - 图中每个边都有一个方向,例如社交媒体网站上的关注关系图就是有向图。
- 无向图 - 图中每个边都没有方向,例如朋友之间的相互认识关系图可以是无向图。
- 简单图 - 没有自环和重复边的无向图或有向图,例如一张不允许两个人之间有多个好友关系的朋友关系图就是简单图。
- 多重图 - 允许存在重复边的无向图或有向图,例如同一个用户在不同时间对同一篇文章进行多次评论的评论关系图就是多重图。
- 完全图 - 任意两个顶点之间都存在一条边的图,例如五个节点的完全图就具有10条边。
- 子图 - 从原图中选取一部分节点和它们之间的边形成的图,例如从一张社交网络上选取几个用户和他们之间的好友关系形成的子图。
- 连通图和联通分量 - 在无向图中,如果任意两个节点之间都存在至少一条路径,则该图为连通图。如果将连通图中所有连通的子图都提取出来,得到的每个连通的子图称为联通分量。
- 强连通图 - 在有向图中,如果任意两个节点之间都存在至少一条有向路径,则该图为强连通图。
- 生成树 - 连通图中的一棵树,它包含了原图中所有节点,并且只有最少的边被保留,例如一个城市的道路系统可以被看做是一张无向图,其最小生成树表示了连接城市的最短路径。
- 度 - 节点拥有的边的数量,对于无向图而言就是与该节点相邻的节点的数量,对于有向图而言则分为入度和出度。
- 权和网 - 图中边具有的权重或者是节点之间的关联程度,例如一个城市之间的距离可以被看做是一张加权无向图。
- 稠密图和稀疏图 - 用来描述图中边的数量相对于节点数量的性质,如果边数接近节点数的平方,那么图就是稠密图;反之,则为稀疏图。
- 路径和路径长度 - 从起始节点到结束节点所经过的边的序列称为路径,路径上经过的边的数量称为路径长度。
- 距离 - 两个节点之间的最短路径长度。
- 回路 - 从起始节点到结束节点的路径,且起始节点和结束节点是同一个节点。在无向图中也被称为环。
二.图的存储
1.邻接矩阵
邻接矩阵是一种用二维数组表示图的数据结构,其中矩阵中的每个元素表示两个节点之间是否存在边。对于无向图而言,邻接矩阵是对称的;对于有向图而言,则不一定对称。
在C语言中,可以使用二维数组来实现邻接矩阵,例如:
#define MAX_NODES 100
int graph[MAX_NODES][MAX_NODES];
其中,graph[i][j] 表示从节点 i 到节点 j 是否存在一条边。如果存在,则该值为1,否则为0。
2.邻接表
邻接表是由顶点和与之相连的边组成的链表,在链表中存储了每个节点的邻居节点信息。对于稀疏图而言,邻接表比邻接矩阵更加节省空间,但查询某个节点的邻居节点需要遍历整个链表。
在C语言中,可以使用结构体和指针来实现邻接表,例如:
#define MAX_NODES 100
struct AdjNode {
int dest;
struct AdjNode* next;
};
typedef struct AdjNode AdjNode;
struct Graph {
AdjNode* adjLists[MAX_NODES];
};
typedef struct Graph Graph;
其中,Graph 结构体包含了一个数组 adjLists,每个元素都是一个指向 AdjNode 结构体的指针。在 AdjNode 结构体中,dest 表示目标节点的编号,next 则是指向下一个邻居节点的指针。
3.关联矩阵
关联矩阵是一种用二维数组表示图的数据结构,其中矩阵中的每个元素表示一个顶点和一条边之间的关系。在关联矩阵中,行代表顶点,列代表边,如果该顶点与该边相连,则值为1,否则为0。
在C语言中,可以使用二维数组来实现关联矩阵,例如:
#define MAX_NODES 100
#define MAX_EDGES 200
int matrix[MAX_NODES][MAX_EDGES];
其中,matrix[i][j] 表示顶点 i 是否与边 j 相连。如果相连,则该值为1;否则为0。
4.十字链表
十字链表是在邻接表的基础上进一步扩展的数据结构,它可以表示有向图的结构,同时避免了邻接表中查询源点和目标点的缺点。在十字链表中,每个节点都有两个域,分别指向以该节点为起点的出边和以该节点为终点的入边。
在C语言中,可以使用结构体和指针来实现十字链表,例如:
#define MAX_NODES 100
struct Edge {
int from;
int to;
struct Edge* nextOut;
struct Edge* nextIn;
};
typedef struct Edge Edge;
struct Graph {
Edge* edges[MAX_NODES];
};
typedef struct Graph Graph;
其中,Graph 结构体包含了一个数组 edges,每个元素都是一个指向 Edge 结构体的指针。在 Edge 结构体中,from 表示边的起点,to 表示边的终点,nextOut 则是指向下一条以该节点为起点的出边的指针,nextIn 则是指向下一条以该节点为终点的入边的指针。
5.前向星
前向星也是在邻接表的基础上进行扩展,它可以同时支持有向图和无向图,同时也解决了在邻接表中查询某个节点的所有出边或入边的效率问题。在前向星中,每个节点不再只存储一个指向第一个邻居节点的指针,而是存储一组指向所有邻居节点的指针,这些指针按照一定的顺序排列成一个链表。
在C语言中,可以使用结构体和数组来实现前向星,例如:
#define MAX_NODES 100
#define MAX_EDGES 200
struct Edge {
int to;
int weight; // 可选
int next; // 指向下一条出边或入边
};
typedef struct Edge Edge;
struct Graph {
Edge edges[MAX_EDGES];
int head[MAX_NODES]; // 存储每个节点的第一条边的编号
int edgeCount;
};
typedef struct Graph Graph;
其中,Graph 结构体包含了两个数组,edges 数组存储所有边的信息,head 数组存储每个节点的第一条边的编号,edgeCount 表示边的数量。在 Edge 结构体中,to 表示边的终点,weight 表示边的权值(可选),next 表示与该边起点相同的下一条边的编号。
6.邻接多重表
邻接多重表是一种用于表示无向图的数据结构,它将每条边都存储为两个顶点之间的一条边,并且对于每个节点存储所有与该节点相连的边的信息。在邻接多重表中,每个节点都有一个指向第一条与该节点相连的边的指针,而每条边则包含了指向其起点和终点下一条边的指针。
在C语言中,可以使用结构体和指针来实现邻接多重表,例如:
#define MAX_NODES 100
#define MAX_EDGES 200
struct Edge {
int from;
int to;
int nextFrom; // 指向起点相同的下一条边
int nextTo; // 指向终点相同的下一条边
};
typedef struct Edge Edge;
struct Graph {
Edge edges[MAX_EDGES];
int head[MAX_NODES]; // 存储每个节点的第一条边的编号
int edgeCount;
};
typedef struct Graph Graph;
其中,Graph 结构体包含了两个数组,edges 数组存储所有边的信息,head 数组存储每个节点的第一条边的编号,edgeCount 表示边的数量。在 Edge 结构体中,from 和 to 分别表示边的起点和终点,nextFrom 和 nextTo 则分别指向与该边起点相同和终点相同的下一条边的编号。
三.图的基本操作
在考研范围内,需要掌握以下图的基本操作:
- 创建图:根据实际需求创建一个空的图数据结构,并初始化各个节点和边的相关信息。
- 添加节点:向图中添加一个新的节点,并更新与该节点相连的所有边的信息。
- 添加边:向图中添加一条新的边,并更新相应节点的邻居节点列表。
- 删除节点:从图中删除一个节点,并将其所有与之相连的边移除。
- 删除边:从图中删除一条边,并更新相应节点的邻居节点列表。
- 查找节点:查找图中是否包含某个特定的节点,并返回其相关信息。
- 查找边:查找图中是否包含某条特定的边,并返回其相关信息。
- 遍历图:遍历图中的所有节点和边,以便进行进一步的分析和处理。
- 拓扑排序:对有向无环图进行拓扑排序,以确定所有节点的执行顺序。
- 最短路径:计算两个节点之间的最短路径,以便找到最优解决方案。
- 最小生成树:寻找无向图的最小生成树,以获得最小成本的连接方式。
四.核心功能实现
1.创建图
// 创建邻接矩阵表示的无向图
void CreateGraph(Graph *G) {
int i, j, k, weight;
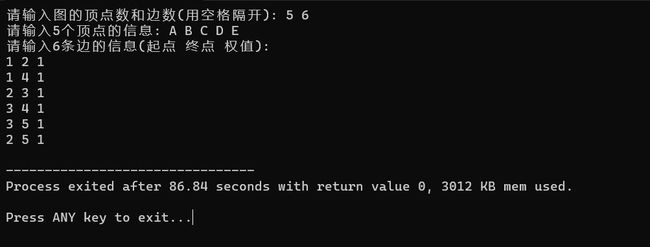
printf("请输入图的顶点数和边数(用空格隔开): ");
scanf("%d %d", &G->vertex_num, &G->edge_num);
printf("请输入%d个顶点的信息: ", G->vertex_num);
for (i = 0; i < G->vertex_num; ++i)
scanf("%s", &G->vertex[i]);
for (i = 0; i < G->vertex_num; ++i)
for (j = 0; j < G->vertex_num; ++j)
G->edge[i][j] = 0; // 初始化邻接矩阵
printf("请输入%d条边的信息(起点 终点 权值):\n", G->edge_num);
for (k = 0; k < G->edge_num; ++k) {
scanf("%d %d %d", &i, &j, &weight);
// 因为是无向图,所以需要对称赋值
G->edge[i][j] = weight;
G->edge[j][i] = weight;
//如果这里是创建有向图,那么就需要我们应该会改
}
}
2.插入顶点
// 在图G中插入顶点x
void InsertVertex(Graph *G, char x){
if(G->vertex_num == MAX_VERTEX_NUM){ // 图已满
printf("Error: 超出最大结点范围\n");
return;
}
G->vertex[G->vertex_num] = x;
G->vertex_num++;
//更新边信息
for(int i=0;i<G->vertex_num-1;++i){
G->edge[i][G->vertex_num-1] = 0; //初始化新顶点的出边
G->edge[G->vertex_num-1][i] = 0; //初始化新顶点的入边
}
}
3.删除顶点
// 将数组中从 start 开始的元素向前移动一位
void moveArray(char arr[], int start, int end) {
for (int i = start; i < end; ++i) {
arr[i] = arr[i+1];
}
}
// 在图G中删除顶点x
void DeleteVertex(Graph *G,char x){
int n = -1; //待删除结点在数组里的下标
for(int i=0;i<G->vertex_num;i++){
if(G->vertex[i]==x) {
n=i;
break;
}
}
if(n == -1){ // 如果节点不存在
printf("Error: 结点不存在\n");
return;
}
// 删除该节点对应的行和列
for(int i=n;i<G->vertex_num-1;++i){
moveArray(G->vertex, i, G->vertex_num - 1); // 将后面的节点前移
for(int j=0;j<G->vertex_num;++j){
G->edge[i][j] = G->edge[i+1][j]; // 前移一位
G->edge[j][i] = G->edge[j][i+1];
}
}
G->vertex_num--;
// 更新最后一行和最后一列
for(int i=0;i<G->vertex_num;++i){
G->edge[G->vertex_num][i] = 0; // 删除最后一列
G->edge[i][G->vertex_num] = 0; // 删除最后一行
}
}
4.求第一个邻接点
//求图G中顶点x的第一个邻接点
char FirstNeighbor(Graph *G,char x){
int n = -1; //待查询结点在数组里的下标
for(int i=0;i<G->vertex_num;i++){
if(G->vertex[i]==x) {
n=i;
break;
}
}
if(n == -1){ // 如果查询节点不存在
printf("Error: 结点不存在\n");
}
int count=0;
int nx; //第一个邻接点在数组里的下标
//现在知道了他在第n个,所以我们查询边矩阵第n行中第一个1在哪就知道第一个邻接点是谁
for(int j=0;j<G->vertex_num;j++){
if(G->edge[n][j]==1) count++;
if(count==1){
nx=j;
break;
}
}
return G->vertex[nx];
}
5.求其余邻接点
//返回图G中顶点x除顶点y的下一个邻接点
char NextNeighbor(Graph *G,char x,char y){
int n = -1; //待查询结点在数组里的下标
for(int i=0;i<G->vertex_num;i++){
if(G->vertex[i]==x) {
n=i;
break;
}
}
if(n == -1){ // 如果查询节点不存在
printf("Error: 结点不存在\n");
}
int count=0;
int nx; //存放返回邻接点数组下标
for(int j=0;j<G->vertex_num;j++){
if(G->edge[n][j]==1){
if(G->vertex[j]!=y){
j=nx;
}
}
}
return G->vertex[nx];
}
6.判断边
//判断图G中x和y之间是否有边
int Adjacent(Graph *G,char x,char y){
int n1,n2; //分别存储x和y的下标
for(int i=0;ivertex_num;i++){
if(G->vertex[i]==x) {
n1=i;
break;
}
}
for(int i=0;ivertex_num;i++){
if(G->vertex[i]==x) {
n2=i;
break;
}
}
if(G->edge[n1][n2]==0 && G->edge[n2][n1]==0)
return -1;
else
return 1;
}
以上部分均选取第三部分比较难 的算法进行实现
五.C语言完整代码
#include 六.运行结果
刚好最近复习数据结构与算法,顺便参加了英杰的新星计划,这是本周第一篇投稿。