【EKF】卡尔曼滤波的一维应用实例
前言
推导了卡尔曼滤波的原理之后,使用一个简单的一维应用实例来训练一下,加深印象。使用一个温度测量的实例来说明,系统的状态方程为:
X(k) = A*X(k-1) + B*u(k-1) + w(k-1)
Z(k) = H*X(k) + v(k)
其中 w 为过程噪声,方差为Q, v 为测量噪声,方差为R
对一维系统来说,协方差矩阵P = 状态X与估计值X_hat的方差 注意:P≠Q
一维协方差矩阵的理解
结合协方差矩阵的定义:
对一维来说,可以理解为状态 x 与估计值 x_hat 之间的方差,需要注意的是:
一维协方差矩阵 P 的值 不等于 过程噪声的方差 Q;
另外,协方差矩阵 P 是不断更新的,过程噪声的方差 Q 是固定的,与建模的过程有关
matlab程序编写
首先进行参数的设定,假设采集一个室内的温度,每 1min 采集一次,一共采集 1000 次数据,初始真实温度是 30度,期间室内温度可以变化,也可以不变化,自己调整,过程噪声 w 的方差为 Q,假设为 0.1^2,注意方差的定义:
温度计的测量噪声 v 的方差为 R,假设为1.0^2。
对于此一维的系统,矩阵 A = 1,H = 1,B = 0。
再加上卡尔曼滤波需要用到的,先验协方差矩阵 P_,协方差矩阵 P,先验估计状态 x_hat,估计状态 xhat,测量值 z,将上述的参数汇总进行初始化工作:
N = 1000; %采样个数 每1min采样一次,采样100min
temp_real = 30; %实际温度 30度
%系统状态方程为:
% X(k) = A*X(k-1) + B*u(k-1) + w(k-1)
% Z(k) = H*X(k) + v(k)
% 其中 w 为过程噪声,方差为Q, v 为测量噪声,方差为R
% 对一维系统来说,协方差矩阵P = 状态X与估计值X_hat的方差 注意:P≠Q
A = 1; %由于是一维系统,因此A矩阵为1
B = 0;
H = 1; %由于是一维系统,因此H矩阵为1
Q = 0.1^2; %假定过程噪声的方差为0.1*0.1
R = 1.0^2; %假定测量噪声的方差为0.5*0.5
x_real = temp_real*ones(1,N); %将实际值赋值到N维数组中
x_hat = zeros(1,N); %先验估计值
xhat = zeros(1,N); %估计值
z = zeros(1,N); %温度计测量值
P = zeros(1,N); %协方差矩阵
P_ = zeros(1,N); %先验协方差矩阵
z(1) = 29.8; %初始测量温度
x_hat(1) = z(1); %初始估计值
P(1) = Q; %初始协方差,指定为Q
w = sqrt(Q)*randn(1,N); %过程噪声 方差的开方就是噪声的大小
v = sqrt(R)*randn(1,N); %测量噪声 方差的开方就是噪声的大小卡尔曼滤波的五大公式:
假设真实温度不变
之后,假设真实温度是不变的,按照卡尔曼滤波的公式进行程序编写:
for k = 2:N
%修改实际值,让真实温度每次递增 但增量需要在方差以内
%x_real(k) = x_real(k-1) + w(k);
%获取测量值
z(k) = H * x_real(k) + v(k); %加入测量噪声
%计算先验估计值
x_hat(k) = A * xhat(k-1);
%计算先验协方差
P_(k) = A * P(k-1) * A' + Q;
%计算卡尔曼增益
K = (P_(k) * H') / (H * P_(k) * H' + R);
%计算后验估计值
xhat(k) = x_hat(k) + K * (z(k) - H * x_hat(k));
%更新估计误差协方差
P(k) = (1 - K * H) * P_(k);
end之后将图形画出来:
绿色为测量值,红色为估计值,蓝色为实际值。
假设真实温度变化
在上述代码中,将真实温度赋值的代码注释去掉即可:
%修改实际值,让真实温度每次递增 但增量需要在方差以内
x_real(k) = x_real(k-1) + w(k);这里的 w 的过程噪声方差的开方值范围的随机数,过程噪声就是建立系统模型过程中造成的误差,因此,如果实际值要增加,也需要满足过程噪声方差的约束条件,否则就会造成卡尔曼滤波跟踪效果不好。
也就是说,我们选取了过程噪声的方差 Q = 0.1^2 ,假设实际温度变化超过了 0.1,那么我们上面建立的模型就跟实际对不上了,我们上述建立的模型是:
X(k) = A*X(k-1) + w(k-1) w方差为Q
实际中的 w 的方差并不是Q,因此卡尔曼滤波器就会效果不好
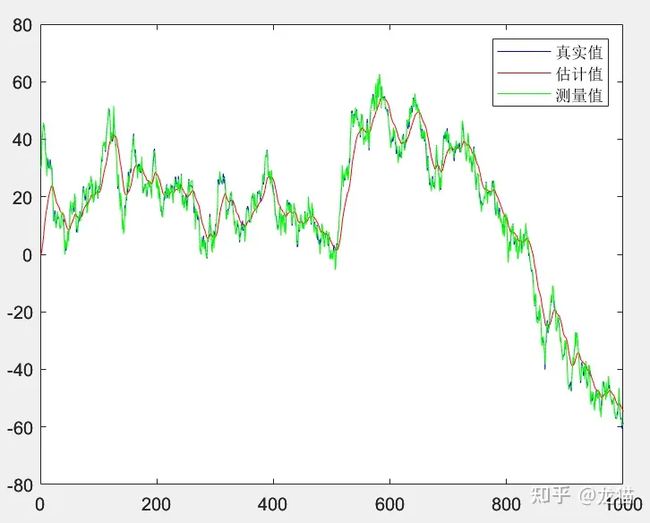
看一下温度在变化时,卡尔曼滤波器的跟踪图:
跟踪效果还是可以的。
过程噪声方差Q的影响
在实际中,测量噪声 v 的方差是比较容易得到的,因为是传感器的方差,可以预先测量 n 组数据来计算出来,计算出的方差 R 与真实方差也是接近的,但过程噪声方差 Q 是比较难确定的,它是由建模引起的,需要实际判断与调试。
假设我们将上面代码中的真实温度变化的范围放大到确定的 Q 之外,再看卡尔曼滤波的跟踪效果,就会比较清楚:
x_real(k) = x_real(k-1) + 30*w(k);这里,将随机数扩大了30倍,可以看到跟踪效果就没有那么好了: