【夜深人静学习数据结构与算法 | 第六篇】贪心算法

目录

前言：

引入:

贪心算法：    

455. 分发饼干 - 力扣（LeetCode）

376. 摆动序列 - 力扣（LeetCode）

53. 最大子数组和 - 力扣（LeetCode）

122. 买卖股票的最佳时机 II - 力扣（LeetCode）

---

前言：

        在本文我们将为大家介绍在计算机中比较常见的一种算法：贪心算法。他并没有具体的代码实现后者是方法套路，而是一种简单，高效的思维方式，因此需要我们以学习思维方式为辅，练习题目为主，这样才可以更加高效的掌握贪心算法。

引入:

         请各位思考一下：如果我们想要在大学的期末考试中取得一个好成绩，我们应该怎么办呢？我们应该学好每一课，那又要如何学好每一科呢？那就要每一节课认真听讲，做好练习。换句话来讲：我们要想取得好的成绩，就要每一天都达成一个最好的学习状态。而在这之中，就蕴藏着贪心算法的思想：通过一个个局部最优解达成全局最优解

贪心算法：    

        贪心算法（Greedy Algorithm）是一种简单而常见的算法思想。它的基本思想是在每一步选择中都采取在当前状态下最好或最优的选择，从而希望导致结果是全局最优或最好的算法。贪心算法的优点是简单、高效，适用于一些特定问题的求解。

        贪心算法一般分为两种类型：纯贪心和分数规划贪心。前者的策略是每次选择当前看起来最优的决策，而后者则是将问题转化为一系列子问题，每个子问题都能通过贪心算法得到最优解，从而构造出全局最优解。

        贪心算法虽然简单易懂，但并不是所有问题都适合用贪心算法求解。有时候贪心策略下的局部最优解可能并不是全局最优解，需要通过其他算法来优化解决方案。

假设此时你的面前有一堆钞票，你只能取十张，那么如何取十张之后得到的金额最大呢？

        只需要每一次都取单张面额最大的纸币，这样我们连续取十张之后，就可以得到最大的金额，这种在通过一个个局部最优解达成全局最优解的策略，就是贪心算法。 

        贪心算法类的题目就像是英语的阅读题一样他无固定套路，没有固定的局部最优解，很多题要么一眼有思路，要么很难想出思路，而不同题目之间的局部最优解也没有什么共通性，只能通过多刷题和多见题来掌握贪心算法。

 我们在下面就通过力扣算法题来给向大家展示贪心算法

455. 分发饼干 - 力扣（LeetCode）

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

 解题思路：想要达到喂饱更多的小孩这个全局最优解，我们就要想到：只要喂给每一个孩子的饼干都是最符合他的就可以达到这个目标，例如此时我们有 5  8  两个孩子，有6，9两个饼干，我们如果把6饼干喂给5小孩，把9喂给8小孩就可以维保两个孩子，但是如果把9喂给5小孩，那8小孩就无法喂饱，也就无法达成喂饱小孩最多的目标。也就是我们尽量用大饼干喂大胃口小孩，小饼干喂小胃口小孩

class Solution {
public:
    int findContentChildren(vector& g, vector& s) {
        sort(s.begin(), s.end(), greater());
        sort(g.begin(), g.end(), greater());
        
        int count = 0;
        int j = 0;
        int i = 0;
        while (i < g.size() && j < s.size()) {
            //此前饼干可以喂饱孩子
            if (s[j] >= g[i]) {
                count++;
                i++;
                j++;
            } 
            //饼干喂不饱孩子
            else {
                i++;//换下一个孩子
                //此时不换饼干是因为饼干大小排序是从大到小，
                //既然此时的饼干已经无法喂饱当前小孩，那后面的饼干也不可能喂饱，因此只用看下一个小孩。
            }
        }
        return count;
    }
};

看到这里大家可能会想：不是吧，这种简单思路还要专门建立一个算法种类。其实不然，贪心算法题就是两个极端：简单的题很简单，难的题很难。感兴趣的同学可以搜索一下力扣968题：监督二叉树，可以说是比较典型的一道贪心算法难题

376. 摆动序列 - 力扣（LeetCode）

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

题目中举的这个例子不明显，我们自己定义一个数组来看：

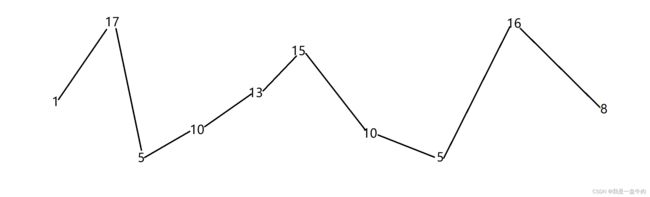
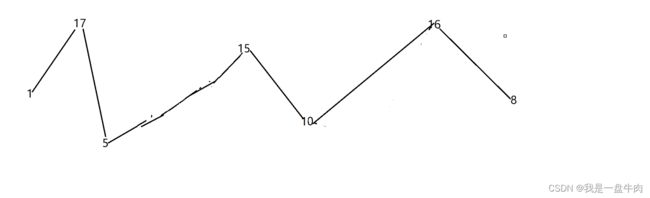
[1,17,5,10,13,15,10,5,16,8]

 

如果我们想要达到差值始终正负出现，我们就删掉所有的单调子数组。

这样我们就可以得到最长的摆动序列，但其实这只是一个底层思路

实际上，我们连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）

这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点

代码实现：

class Solution {
public:
    int wiggleMaxLength(vector& nums) {
        if (nums.size() <= 1) return nums.size();
        int curDiff = 0; // 当前一对差值
        int preDiff = 0; // 前一对差值
        int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值
        for (int i = 0; i < nums.size() - 1; i++) {
            curDiff = nums[i + 1] - nums[i];
            // 出现峰值
            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
                result++;
                preDiff = curDiff; // 注意这里，只在摆动变化的时候更新prediff
            }
        }
        return result;
    }
};

53. 最大子数组和 - 力扣（LeetCode）

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

解题思路：我们要想达成子数组和最大这个全局最优解，就要达到每一步是符合要求内的最大值，其实很好理解： sum=sum+nums[i],我们要想使得sum最大，就应该尽量保证他不是负数，换句话说：我们如果前面的sum已经是一个负数了，负数+num[i],那么我们就抛弃sum[i],让子数组的头从sum[i]重新开始这样往后面看并且添加一个计数器，记录最大的sum，最终返回这个计数器就可以，这样就可以一个for循环结束满足整个要求，大大降低了时间复杂度。

class Solution {
public:
    int maxSubArray(vector& nums) {
      
        int sum=0;
        int i=0;
        int count=INT32_MIN;;
        while(icount)
              {
                count=sum;
              }
                continue;
            }
            sum=sum+nums[i];
            i++;
            if(sum>count)
            {
                count=sum;
            }
        }
        return count;
    }
};

122. 买卖股票的最佳时机 II - 力扣（LeetCode）

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

 解题思路：我们要想总收益最高，那么就是只获得正收益，股票价格一跌就赶紧出手，这样就可以得到最高的收益，在这个题里面就是如果第二天亏损，那么我们就出售股票，如果第二天赚钱，我们就买入股票。

例如我们的例题：

        7 1 5 3 6 4

        第二天：价格为1，相比昨天下降6元

        第三天：价格为5，相比昨天上涨五元

        第四天：价格为3，相比昨天亏损二元（既然亏损，那么我们就五元的时候卖出，就可以得到正收益。）

        第五天：价格为6，相比较昨天上涨三元(既然上涨我们就在昨天三元买入)

        第六天：价格为4，相比较昨天下跌四元（既然下跌我们就在昨天六元的时候卖出）

 我们只需要收集正收益就可以了，甚至不用记录哪一天买入,只需要一个数组存储正收益，后面把正收益一加起来就好了。

class Solution {
public:
    int maxProfit(vector& prices) {
        vectord1;
        int sum=0;
        for(int i=0;i0)
            {
                sum+=a;
            }
        }
        return sum;
    }
};

总结：

        贪心算法是一种解题思路，他没有套路可以总结，没有解题模板，没有固定格式，但是在一些题中，如果我们可以利用贪心算法思路把这道题的头绪理清楚，那么代码将会是很简洁高效的，因此希望大家可以多刷一些关于贪心算法的题目。

如果我的内容对你有帮助，请点赞，评论，收藏。创作不易，大家的支持就是我坚持下去的动力！