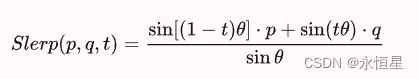对球面线性插值的理解

【前言】

线性插值是点A到点B间距离的均匀变化，球面线性插值是点A到点B的角度均匀变化，前者应用范围很广，后者主要应用平滑旋转

【球面线性插值求解】

球面线性插值（Spherical linear interpolation，Slerp）也可以写成如下形式：

Y = a(t)Y0 + b(t)Y1 

需要求解的是a(t)，b(t)

以Vector3为例：此时将点看作向量，已经有两个向量A和B（已知向量方向和长度），求新的向量C的方向和长度，其中C和A形成的角度是线性变化的。

先求方向：先将向量单位化

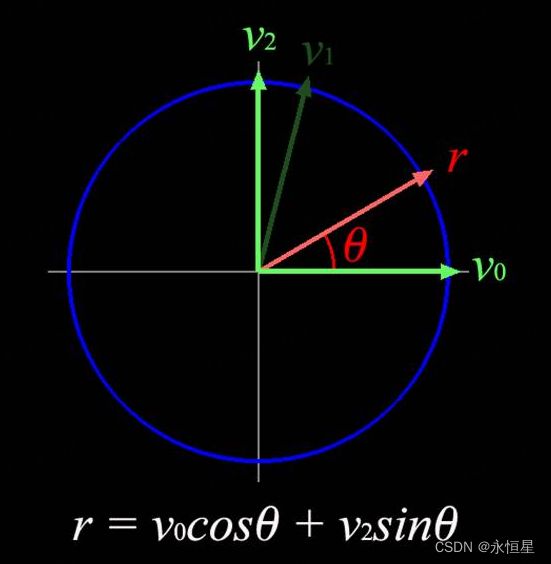
 图中v0和v1表示AB向量，v2垂直v0，r是待求的向量方向，θ是r的旋转角度，可得：

r = v0cosθ + v2sinθ.

这里只有v2未知，设v1在v0的投影向量为v3，那么v3 = （v1*v0)*v0，v2 = Normalize(v1 - (v0 · v1)v0)

再求长度：

上述求得的向量长度为1，新向量的长度是多少呢？可以根据自己的需求来设置。常用的有两种方式

一是：向量C所在的点在AB所在的直线上

二是：向量C的长度为向量A和B的长度的线性插值

后者即为Unity中的Vector3.Slerp

采用后者求长度的代码为：

Vector3 Slerp(Vector3 start, Vector3 end, float percent)
    {
        Vector3 startNormal = start.normalized;
        Vector3 endNormal = end.normalized;
        float dot = Vector3.Dot(startNormal, endNormal);
        Mathf.Clamp(dot, -1.0f, 1.0f);
        float theta = Mathf.Acos(dot) * percent;
        Vector3 RelativeVec = endNormal - startNormal * dot;
        RelativeVec.Normalize();
        Vector3 result = (startNormal * Mathf.Cos(theta) + RelativeVec * Mathf.Sin(theta));
        float length = start.magnitude * (1- percent) + end.magnitude *  percent;
        return length * result;
    }

 【四元数的球面线性插值】

我们知道四元数也可以表示方向，即旋转角度。也可以用四元数做球面线性插值，使得角度的均匀变化。其结果为：

推到过程见链接。

【Nlerp】

Vector3.Slerp的计算涉及三角函数和求长度，耗时较长，当向量的长度为1时可以采用近似的方式实现球面线性插值，这就是Nlerp，多应用与动画。

Vector3 NLerp(Vector3 start, Vector3 end, float percent)
    {
        return Vector3.Lerp(start, end, percent).normalized;
    }

【参考】

Math Magician – Lerp, Slerp, and Nlerp – Keith M. Programming

四元数的球面线性插值（slerp） - 知乎

https://www.cnblogs.com/21207-iHome/p/6952004.html