算法练习 DAY21 || 530.二叉搜索树的最小绝对差 501.二叉搜索树中的众数 236. 二叉树的最近公共祖先
530.二叉搜索树的最小绝对差
给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。
注意，题目中给出的是一个二叉搜索树，是有序的！
递归方法一
所以只要转换成一个有序数组（中序遍历），统计相邻下标的数的差值，就能找到最小差值。
上图二叉树转换成数组以后：0 1 12 48 49。虽然题目中要求任意两节点的最小差值，对于一个有序数组而言，相邻差值比如0 1一定比跳跃的差值0 12要小。
class Solution {
public:
vector<int> vec;
void traversal(TreeNode* cur) {
if (cur == nullptr) return;
traversal(cur->left);
vec.push_back(cur->val);// 将二叉搜索树转换为有序数组
traversal(cur->right);
}
int getMinimumDifference(TreeNode* root) {
int result = INT_MAX;
vec.clear();
traversal(root);
for (int i = 0; i < vec.size()-1; i++) {// 统计有序数组的最小差值
result = min(vec[i + 1] - vec[i], result);
}
return result;
}
};
递归方法二
/* 递归方法二
一边遍历一边求差值
只要把当前节点的前一个节点存放一下就可以了
*/
class Solution1 {
public:
TreeNode* pre;
int result = INT_MAX;
void transform(TreeNode* cur) {
if (cur == nullptr) return;
transform(cur->left); //左
if (pre != nullptr && cur->val - pre->val < result) result = cur->val - pre->val;
pre = cur; //记录前一个节点 //中
transform(cur->right); //右
}
int getMinimumDifference(TreeNode* root) {
transform(root);
return result;
}
};
501.二叉搜索树中的众数
给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。
假定 BST 有如下定义：
结点左子树中所含结点的值小于等于当前结点的值
结点右子树中所含结点的值大于等于当前结点的值
左子树和右子树都是二叉搜索树
返回[2].
提示：如果众数超过1个，不需考虑输出顺序
进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）
普通二叉树
遍历二叉树 把值和出现的次数放进map
对map的velue排序 返回最大的那几个即可
class Solution1 {
public:
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历
if (cur == nullptr) return;
map[cur->val]++; //中 // 统计元素频率
searchBST(cur->left,map);
searchBST(cur->right,map);
}
bool static cmp(pair<int, int>& a, pair<int, int>& b) {
return a.second > b.second;
}
vector<int> findMode(TreeNode* root) {
vector<int> result;
if (root == nullptr) return result;
unordered_map<int, int> map; // key:元素，value:出现频率
map.clear();
searchBST(root, map);
//但是由于不能对map的velue直接进行排序，所以把map转成vector再进行排序
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp);//排序
result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {
if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
else break;
}
return result;
}
};
搜索二叉树
依旧是使用双指针，记录前一个节点和当前节点
使用中序遍历 这样所有数都是按照从小到大的顺序进行排序
那么相等的数就会被凑到一起，在便利的时候
两个节点作比较 更新当前val的次数count
然后把当前count与maxCount作比较
！！！注意
count > maxCount的话 就要把之前vec里面存放的众数清空了
class Solution2 {
public:
int maxCount = 0;
int count = 0;
vector<int> result;
TreeNode* pre;
void traversal(TreeNode* cur) {
if (cur == nullptr) return;
traversal(cur->left); //左
//处理"中" 也就是单层逻辑
if (pre == nullptr) { //遍历到最左边那个叶子
count = 1;
}
else if (pre != nullptr && cur->val == pre->val) { //如果这个值和上一个相同
count++;
}else{ //与上一个不同 那么count就从头统计
count = 1;
}
//这个节点的val处理完毕，开始判断到这个节点为止count和maxcount的关系
if (count > maxCount) {
maxCount = count;
result.clear();
result.push_back(cur->val);
}else if(count == maxCount) result.push_back(cur->val);
pre = cur; //更新前一个节点
traversal(cur->right); //右
}
vector<int> findMode(TreeNode* root) {
result.clear();
if (root == nullptr) return result;
traversal(root);
return result;
}
};
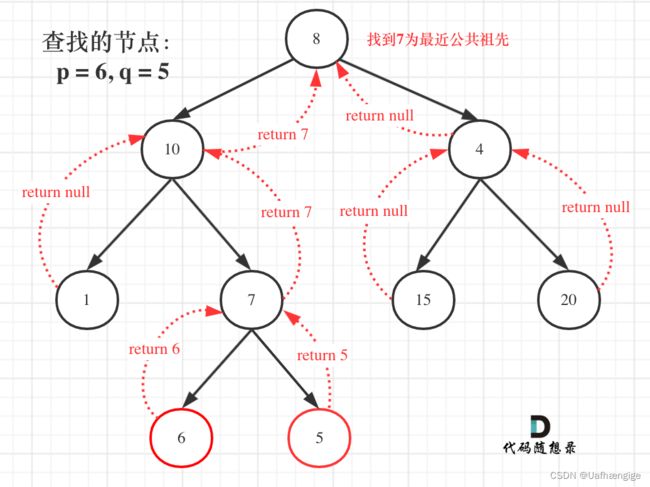
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
class Solution {
public:
/*
关键在于如何确认是不是公共祖先
*/
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr) return nullptr;
if (root == p || root == q) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q); //左
TreeNode* right = lowestCommonAncestor(root->right, p, q); //右
//中
if (left != nullptr&&right != nullptr) return root;
else if (left != nullptr&&right == nullptr) return left;
else if (right != nullptr&&left == nullptr) return right;
else return nullptr;
}
};