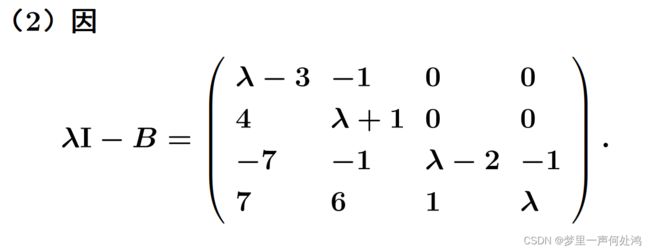高等工程数学 —— 第二章 （1） Smith标准型与Jordan标准型
高等工程数学 —— 第二章 （1） Smith标准型与Jordan标准型
文章目录
- 高等工程数学 —— 第二章 （1） Smith标准型与Jordan标准型
-
- 不变因子与Smith标准型
- 行列式因子
-
- 行列式因子与不变因子的关系
- 初等因子与Jordan标准型
-
- 求Jordan标准型与相似变换矩阵
不变因子与Smith标准型
将某矩阵通过初等行（列）变换，变换规则如下：
注意：
某行（列）只能倍乘常数，只有在加到另一行时能够倍乘含 λ \lambda λ的表达式。你想想，要不形如（0，0， λ \lambda λ）时你全给 λ \lambda λ消成1了。
最后如果能将该矩阵化作如下形式：
- 这里只存在对角线元素有非0元素。其中 d i ( λ ) ∣ d i + 1 ( λ ) d_i(\lambda)|d_{i+1}(\lambda) di(λ)∣di+1(λ)代表 d i ( λ ) d_i(\lambda) di(λ)能够整除 d i + 1 ( λ ) d_{i+1}(\lambda) di+1(λ)。
- 这里对角线后面几个元素可以为0
此时，我们将 d i ( λ ) d_i(\lambda) di(λ)叫做不变因子。上述变换后得到的矩阵称为Smith标准型。
例：
初等变换过程如下：
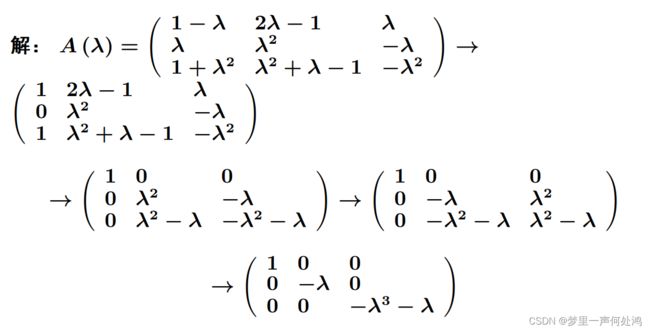
注意：我们需要 d i ( λ ) d_i(\lambda) di(λ)为首项系数为1.
这里我们发现 d i ( λ ) d_i(\lambda) di(λ)能够整除 d i + 1 ( λ ) d_{i+1}(\lambda) di+1(λ)。（例如： λ \lambda λ能够整除 λ 3 + λ \lambda^3+\lambda λ3+λ； λ 3 + λ \lambda^3+\lambda λ3+λ能够被 λ \lambda λ整除）
行列式因子
- 简单说就是把每一阶的行列式值求一下，然后 k k k阶行列式的所有非0值中的最大公因式就是 k k k阶行列式因子的值。
例如：
( λ 2 0 0 0 0 λ 2 − λ 0 0 0 0 ( λ − 1 ) 2 0 0 0 0 λ 2 − λ ) \begin{pmatrix} \lambda^2 & 0 & 0 &0\\ 0 & \lambda^2- \lambda& 0 &0\\ 0 & 0 &(\lambda-1)^2 &0\\ 0 & 0 & 0 &\lambda^2- \lambda\\ \end{pmatrix} ⎝ ⎛λ20000λ2−λ0000(λ−1)20000λ2−λ⎠ ⎞
先取各阶行列式所有的非0值：
4阶： λ 4 ( λ − 1 ) 4 \lambda^4(\lambda-1)^4 λ4(λ−1)4
3阶： λ 3 ( λ − 1 ) 3 ， λ 4 ( λ − 1 ) 2 ， λ 2 ( λ − 1 ) 3 \lambda^3(\lambda-1)^3，\lambda^4(\lambda-1)^2，\lambda^2(\lambda-1)^3 λ3(λ−1)3，λ4(λ−1)2，λ2(λ−1)3
2阶： λ 3 ( λ − 1 ) ， λ 2 ( λ − 1 ) 2 ， λ ( λ − 1 ) 3 \lambda^3(\lambda-1)，\lambda^2(\lambda-1)^2，\lambda^(\lambda-1)^3 λ3(λ−1)，λ2(λ−1)2，λ(λ−1)3
1阶： λ 2 ， λ ( λ − 1 ) ， ( λ − 1 ) 2 \lambda^2，\lambda(\lambda-1)，(\lambda-1)^2 λ2，λ(λ−1)，(λ−1)2
之后我们取各阶最大公因子：
D 4 = λ 4 ( λ − 1 ) 4 D_4 = \lambda^4(\lambda-1)^4 D4=λ4(λ−1)4
D 3 = λ 2 ( λ − 1 ) 2 D_3 = \lambda^2(\lambda-1)^2 D3=λ2(λ−1)2
D 2 = λ ( λ − 1 ) D_2 = \lambda(\lambda-1) D2=λ(λ−1)
D 1 = 1 D_1 = 1 D1=1
其中 D i D_i Di即为行列式因子。
行列式因子与不变因子的关系
可见我们将行列式因子除一下就能得到不变因子：
d 4 = λ 2 ( λ − 1 ) 2 d_4 = \lambda^2(\lambda-1)^2 d4=λ2(λ−1)2
d 3 = λ ( λ − 1 ) d_3 = \lambda(\lambda-1) d3=λ(λ−1)
d 2 = λ ( λ − 1 ) d_2 = \lambda(\lambda-1) d2=λ(λ−1)
d 1 = 1 d_1 = 1 d1=1
因此我们可以求得例题中矩阵的Smith标准型为：
( 1 0 0 0 0 λ ( λ − 1 ) 0 0 0 0 λ ( λ − 1 ) 0 0 0 0 λ 2 ( λ − 1 ) 2 ) \begin{pmatrix} 1 & 0 & 0 &0\\ 0 & \lambda( \lambda-1)& 0 &0\\ 0 & 0 &\lambda( \lambda-1) &0\\ 0 & 0 & 0 &\lambda^2( \lambda-1)^2\\ \end{pmatrix} ⎝ ⎛10000λ(λ−1)0000λ(λ−1)0000λ2(λ−1)2⎠ ⎞
这也为我们提供了一个求解不变因子的便捷方法，如果通过初等行变换那么太慢了且容易出错。
如果我们对于次高阶行列式存在一个不含 λ \lambda λ的常数或者两个不含公因子的行列式值，那么我们取该阶最大公因式的时候就只能取1.之后低阶的最大公因子也只能取1，因为这样才能和次高阶的1整除。
例如：
( λ − 1 − 1 0 − 6 λ − 2 0 0 − 1 λ + 1 ) \begin{pmatrix} \lambda-1 & -1 & 0 \\ -6 & \lambda-2 & 0 \\ 0 & -1 & \lambda+1 \\ \end{pmatrix} ⎝ ⎛λ−1−60−1λ−2−100λ+1⎠ ⎞
其中 D 3 = ( λ + 1 ) 2 ( λ − 4 ) D_3 = (\lambda+1)^2(\lambda-4) D3=(λ+1)2(λ−4)
对于二阶行列式值有 D 13 D_{13} D13 = ∣ 6 λ − 2 0 − 1 ∣ = 6 \begin{vmatrix} 6 & \lambda-2 \\ 0 & -1 \\ \end{vmatrix} = 6 ∣ ∣60λ−2−1∣ ∣=6
所以， D 2 = D 1 = 1 D_2 = D_1 = 1 D2=D1=1。除一下易得不变因子为 ( λ + 1 ) 2 ( λ − 4 ) ， 1 ， 1 (\lambda+1)^2(\lambda-4)，1，1 (λ+1)2(λ−4)，1，1
该方法试用与有较多0元素时，我们可以比较容易得出次高阶行列式是常数的情况。
初等因子与Jordan标准型
初等因子就是将次数大于0的不变因子分解为互不相同的一次因式方幂的乘积。
例如：
不变因子为： ( λ − 1 ) 2 ， ( λ − 1 ) 2 ( λ + 1 ) ， ( λ − 1 ) 2 ( λ + 1 ) ( λ 2 + 1 ) 2 (\lambda-1)^2，(\lambda-1)^2(\lambda+1)，(\lambda-1)^2(\lambda+1)(\lambda^2+1)^2 (λ−1)2，(λ−1)2(λ+1)，(λ−1)2(λ+1)(λ2+1)2
初等因子为： ( λ − 1 ) 2 ， ( λ − 1 ) 2 ， ( λ − 1 ) 2 ， ( λ + 1 ) ， ( λ + 1 ) ， ( λ + i ) 2 ， ( λ − i ) 2 (\lambda-1)^2，(\lambda-1)^2，(\lambda-1)^2，(\lambda+1)，(\lambda+1)，(\lambda+i)^2，(\lambda-i)^2 (λ−1)2，(λ−1)2，(λ−1)2，(λ+1)，(λ+1)，(λ+i)2，(λ−i)2
对于求初等因子我们有以下三种方法：
- 用初等行变换成Smith标准型求不变因子，然后求初等因子
- 用初等行变换成对角矩阵，然后分解对角元素成初等因子
- 化成对角矩阵后不用疑惑为啥没有整除关系，我们这里并没有构造Smith标准型哦
- 该方法就是我之前说的简单方法，不一定每个都能用。
Jordan标准型的求法
第一步就是求出 λ I − A \lambda I - A λI−A的初等因子。
- 只要Jordan块对了就行，顺序可以改变。
例1：
例2：
求Jordan标准型与相似变换矩阵
之后将值代进去然后再设几个 x i x_i xi的值就可得到 P = ( 1 0 0 − 1 − 1 1 2 1 0 ) P= \begin{pmatrix} 1 & 0 &0 \\ -1 & -1 &1 \\2 & 1 & 0 \end{pmatrix} P=⎝ ⎛1−120−11010⎠ ⎞。P是不唯一的哈。