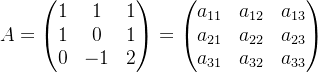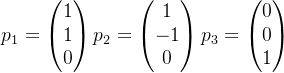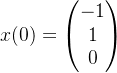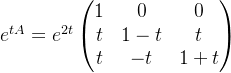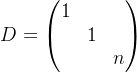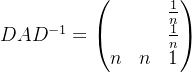矩阵论基础
目录
参考博客
一、线性空间
1.集合和数域
2.线性空间
3.线性相关与线性无关
4.基与维数
5.线性子空间
6.矩阵值域与核
7.矩阵的特征值和特征向量
8.行列式
9.子空间的交与和
10.矩阵的秩和维数
11.矩阵类型
11.Hermite标准型
12.矩阵的亏
13.特征多项式和最小多项式
14.矩阵合同
15.向量正交化
16.正交补
17.不变因子和初等因子
18.矩阵的逆
二、两个空间
1.欧式空间
2.酉空间
3.实内积空间与复内积空间对比
三、矩阵分解
1.特征值分解
2.QR分解
3.正规矩阵及schur分解
4.满秩分解
5.奇异值分解
6.谱分解
四、广义逆矩阵
1. 满秩分解求广义逆
2.奇异值分解求广义逆
3.谱分解求广义逆
4.方程组相容
5.{1}-逆
6.广义逆判断方程是否有解
五、向量与矩阵范数
1.向量范数
2.矩阵范数
3.非齐次线性方程组的解
六、矩阵序列与矩阵函数
1.矩阵函数
2.矩阵函数求解
1.待定系数法
2.Jordan标准型法
3.矩阵微分方程
七、矩阵特征值估计
参考博客
一、线性空间
1.集合和数域
集合指一堆东西放在一起,数域表示里面的数字对加减乘除封闭,属于集合的一个特殊情况,并且无限
2.线性空间
指一个空间,其中的任意一个向量,不论是乘一个常数还是和其他向量进行加减乘除运算,结果还是在这个空间里,则称这个空间为线性空间。与数域概念类似。
3.线性相关与线性无关
若存在一堆向量![]() ,使得
,使得![]() ,其中
,其中![]() 不全为0,则称
不全为0,则称![]() 线性相关。反之则线性无关。
线性相关。反之则线性无关。
线性相关表示这些向量互相之间处于相互垂直状态,在各向量不为0的情况下,向量和绝不会出现0的状况。线性无关则表示这些向量中至少有一个向量与其他向量不垂直。
4.基与维数
线性空间可以由最少的m个向量组合表示所有的向量,则这个最小数m即为线性空间的维数,m维线性空间V记为![]() 。
。
向量坐标含义:线性空间中某向量在各坐标基下的分量,称为该向量的坐标
5.线性子空间
![]() 是是V的一个非空子集合,V是数域空间K上的线性空间,如果
是是V的一个非空子集合,V是数域空间K上的线性空间,如果![]() 满足:
满足:
- 如果x,y

 ,则x+y
,则x+y 
- 如果x

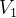 ,k
,k K,则kx
K,则kx
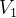
如果 ![]() 和V相等或者为空集,则
和V相等或者为空集,则 ![]() 称为平凡子空间,否则称为非平凡子空间
称为平凡子空间,否则称为非平凡子空间
6.矩阵值域与核
值域(列空间):所有经过矩阵变换的向量,变换后的向量都落在了一个空间里,这个空间叫值域。
记R(A)表示矩阵A的值域,存在任意向量x,使得Ax=y向量,y向量组成的集合叫矩阵A的值域。
![]()
矩阵值域满足:
![]()
核:任意向量进行矩阵变换后,结果为0,这些向量组成的空间为A的核空间,或者零空间。
![]()
核空间的维度称为A的零度,记为n(A)
维数:核所在的空间称为V,V的维数=其变换矩阵的核空间维数+值域的维数。
![]()
矩阵4个空间:任意矩阵都可以分为两个空间 :行空间+零空间或列空间+左零空间
dim(nullspace) = 列数 - r = n - r
dim(left nullspace) = 行数 - r = m - r
7.矩阵的特征值和特征向量
![]()
向量变换:矩阵A可以理解为对向量x做的变换,即A对x做完变换后,x只在长度上进行缩放。
也可以这么理解,有一个矩阵A,怎么找到被它变换后的向量x,只在长度上有变化,方向不变的向量,这些向量就是矩阵A的特征向量,对应的![]() 就是特征值。
就是特征值。
矩阵的所有特征向量组成了矩阵的基,也就是经过矩阵操作后的坐标系。矩阵操作可以理解为对向量的变化,或者对坐标系的变换(也就是基的变换)。
坐标系变换:向量x,乘以矩阵A,变为向量b
![]()
可以理解为向量不变,只是坐标系进行了变换
x是在A坐标系下的描述,b是在I坐标系下的描述,也就是,其中I可看作省略
![]()
例如:在正常二维坐标系下的点(2,3),将其变为点(1,1)有两种方案,一是直接将点移动到后者处,也就是运动;二是将坐标系横轴缩短1/2,纵轴缩短1/3。
矩阵理解:当存在一个线性变换,可以用多个矩阵去描述这个变换,但这些矩阵都不是这个变换本身,只是这个变换的一种描述方式,而这些可以描述此变换的矩阵,都是相似的,具有相同的特征向量和特征值。
8.行列式
矩阵A可以理解为n维空间里,从一个点到另一个点的线性变换。若变换的对象也是一个矩阵T,可以理解为从n维空间到n维空间,对一个立方体T的变换,变换后为M,变换后的体积除以变化前的体积即为变换率,也就是行列式的值。
![]()
![]()
矩阵的逆:矩阵A理解为矩阵从T变为M,矩阵![]() 理解为矩阵从M变回T,则:
理解为矩阵从M变回T,则:
![]()
若矩阵可逆,则必有行列式,也就是变换倍率,若矩阵无行列式,也就说明矩阵必不可逆。
9.子空间的交与和
交为交集,和为并集
直和:![]() 唯一的表示为
唯一的表示为![]() 中的一个向量和
中的一个向量和![]() 中的一个向量和,记为
中的一个向量和,记为![]()
可以理解为,把高维度空间中的一个向量,分别投影到相互正交独立的维度上,对它们处理完后,直和就是该向量要求的解,类似力的分解。
10.矩阵的秩和维数
秩:矩阵的秩=列向量的维数=行向量的维数,也就是列向量张成的最大维度,记为rank(A)
维数:线性空间由几个向量组成,也就是列向量的数目,记为dim(A)
11.矩阵类型
| 实正交矩阵 | |
| 酉矩阵 |
|
| 对称矩阵( |
|
| 厄米特矩阵 | |
| 正规矩阵(一定可相似对角化) | |
| 奇异矩阵 | |
| 幂等矩阵 | |
| 单纯矩阵 | 可对角化的矩阵 |
11.Hermite标准型
矩阵![]() ,且H前r行是非零行,并包含一个单位矩阵
,且H前r行是非零行,并包含一个单位矩阵![]() ,后m-r行全为0。例:
,后m-r行全为0。例:
![]()
12.Jordan标准型
上三角块,例:
12.矩阵的亏
若矩阵满秩,则矩阵的秩![]() ,亏为
,亏为![]()
若矩阵不是满秩的,秩为![]() ,亏为
,亏为![]()
13.特征多项式和最小多项式
(1)特征多项式
n阶矩阵A是其特征多项式的根(零点)
![]()
即满足:
![]()
(2)最小多项式
次数最小的使m(A)=0的特征多项式,首项系数为1。一般求法是参照![]() ,将其最高次幂依次降低1,然后尝试,直到满足m(A)=0
,将其最高次幂依次降低1,然后尝试,直到满足m(A)=0
14.矩阵合同
A与B合同条件:
存在可逆矩阵C,使得![]()
15.向量正交化
若存在一组不共面的向量,如何将其正交化?
思路是先将其中两个向量正交化,然后再将第三个分量与正交的两个分量再做一次正交
16.正交补
若向量y和向量![]() 均正交,则y与
均正交,则y与![]() 的线性组合也正交。
的线性组合也正交。
w为欧式空间![]() 的子空间,若存在向量y与W正交,则y与W的每一个基向量正交。
的子空间,若存在向量y与W正交,则y与W的每一个基向量正交。
正交补:
y称为W空间的正交补,记为
![]()
正交补空间的维数:
![]()
![]()
17.不变因子和初等因子
初等因子、不变因子
不变因子:
smith标准型对角线元素为不变因子,由小到大排列。分别记为![]()
行列式因子![]() 为第k阶子式的最大公因式,且满足
为第k阶子式的最大公因式,且满足![]()
初等因子:
将不变因子常数项去掉,将其余各因子拆分
例:
不变因子:![]()
初等因子:![]()
18.矩阵的逆
矩阵的逆求法1:
![]()
矩阵的逆求法2:
将矩阵A和I并排写,然后同时进行初等行变换,把A化为I,此时I的位置就是![]() ,原理是初等行变换相当于给A左乘了一个矩阵T,使得
,原理是初等行变换相当于给A左乘了一个矩阵T,使得![]() ,所以
,所以![]() ,也就是等于I变换后的矩阵。
,也就是等于I变换后的矩阵。
特征值和特征向量求法:任意矩阵A,求![]()
进行行变换和列变化,使得某一行或某一列只剩一个数,其余全是0,然后该行列式等于该点的值乘以代数余子式。
求矩阵A的伴随矩阵![]() :
:
求对应位置的代数余子式,需要注意的地方是,与原来处的代数余子式需要填到另一个位置,此处需要尤为注意
例:
![]()
二、两个空间
1.欧式空间
实内积空间
内积结果是一个数值
2.酉空间
复内积空间
![]() 表示
表示![]() 的共轭
的共轭
3.实内积空间与复内积空间对比
| 实内积空间 (欧式空间) |
复内积空间(酉空间) | |
| 数 | 实数 | 复数 |
| 正交变换 (正交矩阵)
|
酉变换(酉矩阵)
|
|
| 对称变换(实对称矩阵)
|
厄尔米特变换(酉对称变换)厄尔米特矩阵
|
|
| 矩阵特征值 | 实数 | 实数 |
| 矩阵特征向量 | 正交 | 正交 |
三、矩阵分解
目的:把矩阵分解为一些小矩阵,更易计算,或者更容易分析矩阵的特点
1.特征值分解
![]()
tips:
这里组成P的特征向量不需要施密特正交化即可,施密特正交化只是为了方便求![]() 。比如下面schur分解就使用了施密特正交化,因为施密特正交规范化后,P变为正交矩阵,也就有
。比如下面schur分解就使用了施密特正交化,因为施密特正交规范化后,P变为正交矩阵,也就有![]() 。
。
2.QR分解
定义:实(复)非奇异矩阵A可以分解为正规矩阵Q和正线上三角矩阵R
奇异矩阵:行列式=0的矩阵,即不可逆矩阵
A的列向量为![]()
(1)求矩阵A的正交单位化矩阵,即Q
对![]() 正交化
正交化
其中![]()
![]()
对![]() 单位化
单位化
![]()
![]()
(2)求正交向量模值与C的乘积,即R
例子:
![]()
对![]() 单位化
单位化
Givens矩阵和Givens变换:
Givens矩阵为初等旋转矩阵,由Givens矩阵确定的变换称为Givens变换,也就是初等旋转变换。
性质:
(1)Givens矩阵是正交矩阵
(2)任意可逆矩阵都可以通过左乘有限个Givens矩阵变为上三角矩阵
Householder矩阵:
Householder矩阵也叫初等反射矩阵,相当于对向量或矩阵做镜像,模值不变。
性质:
(3)Givens矩阵是两个Householder矩阵的乘积
(4)任意可逆矩阵都可以通过左乘有限个Householder矩阵变换为上三角矩阵
3.正规矩阵及schur分解
Schur引理:
![]() 且A的特征值均为实数,则存在正交矩阵Q,使得
且A的特征值均为实数,则存在正交矩阵Q,使得
任意实方阵A,正交相似于一个上三角阵,且其主对角线元素为矩阵A的特征值
Schur分解流程:
其原理是,已知![]() ,其中P为满秩矩阵,其实当P为酉矩阵时,此处
,其中P为满秩矩阵,其实当P为酉矩阵时,此处![]() ,因此求酉矩阵P就相当于之前求满秩矩阵P
,因此求酉矩阵P就相当于之前求满秩矩阵P
例子:
求酉矩阵Q,使得![]() 为对角矩阵
为对角矩阵
(1)求特征值对应的特征向量
a.求特征值
当![]() 时
时
当![]() 时
时
当![]() 时
时
(2)将特征向量正交标准化
(3)![]()
4.满秩分解
定义:若![]() ,如果存在
,如果存在![]() 和
和![]() ,使得
,使得![]() ,则称其为矩阵的满秩分解。满秩分解不唯一
,则称其为矩阵的满秩分解。满秩分解不唯一
例子:
![]()
![]()
G就是行最简型
5.奇异值分解
在特征值分解的基础上,衍生出奇异值分解,根本原理相同,只不过特征值分解对应的是![]() 阶矩阵,奇异值分解对应的是
阶矩阵,奇异值分解对应的是![]() 阶矩阵,不是方阵。
阶矩阵,不是方阵。
对于![]() 阶矩阵A,
阶矩阵A,![]() 为
为![]() 阶对称矩阵(对称矩阵
阶对称矩阵(对称矩阵![]() ),
),![]() 为
为![]() 阶对称矩阵,则有
阶对称矩阵,则有
![]()
![]()
P为![]() 的左奇异向量,Q是
的左奇异向量,Q是![]() 的右奇异向量
的右奇异向量
P和T均为酉矩阵,酉矩阵也是正交矩阵,正交矩阵对角化可写作![]()
则
![]() 为A的特征值开方,称为A的奇异值
为A的特征值开方,称为A的奇异值
例:
(1) ![]()
对应特征向量为:
单位化后:
(2)![]()
单位化后:
.
(3)
求解思路:
奇异值分解(SVD)求解过程其实异常简单,由![]() 可以推出以下两个公式:
可以推出以下两个公式:
![]()
所以奇异值分解其实很简单,把![]() 和
和![]() 当成一个方阵进行shur分解,也就是求特征值对应的标准正交基,若A是m*n阶矩阵,则
当成一个方阵进行shur分解,也就是求特征值对应的标准正交基,若A是m*n阶矩阵,则![]() 对应U,
对应U,![]() 对应V的求解,并且他们的特征值相同。
对应V的求解,并且他们的特征值相同。
6.谱分解
定义:单纯矩阵(可对角化矩阵)A,可以分解为特征值与幂等矩阵积的和,即
![]()
![]() 称为A的谱值,也就是A的特征值,
称为A的谱值,也就是A的特征值,![]() 称为A的谱阵
称为A的谱阵
所以,谱分解,其实可以看做矩阵的特征值分解,将矩阵分解为单个特征值和单个矩阵的乘积和。
特征值分解,记为![]()
求解思路:
(1)求特征值和特征向量
(2)将特征向量规范化,即求P和![]()
(3)分解P和![]() 求
求![]()
例:
特征值分别为![]() ,
,![]()
![]()
![]()
四、广义逆矩阵
对应下面一二两公式。
设矩阵![]() ,若矩阵
,若矩阵![]() 满足以下某个或全部
满足以下某个或全部
则称X为A的广义逆矩阵。若4个都满足,称X为A的Penrose逆,记为![]()
1. 满秩分解求广义逆
若![]() ,则
,则
![]()
因此需要先求满秩分解![]()
2.奇异值分解求广义逆
若![]() ,
,![]() 则
则
![]()
3.谱分解求广义逆
4.方程组相容
定义:存在非齐次线性方程组![]()
若![]() ,则称此线性方程组相容
,则称此线性方程组相容
5.{1}-逆
![]()
![]()
6.广义逆判断方程是否有解
判断![]() 是否有解
是否有解
若![]() ,则有解
,则有解
五、向量与矩阵范数
![]() ,向量x的范数表示向量的大小,矩阵A的范数表示从向量x变为向量b时变化的倍率,也就是缩放量的大小,范数是个大小度量工具。
,向量x的范数表示向量的大小,矩阵A的范数表示从向量x变为向量b时变化的倍率,也就是缩放量的大小,范数是个大小度量工具。
1.向量范数
| 类别 | 公式 | 含义 |
| 1-范数 | x绝对值之和 | |
| 2-范数 | x欧氏距离 | |
| x绝对值中最大 | ||
| p-范数 | x的p次方和开 |
|
| E-范数 | 与2-范数差了绝对值 |
2.矩阵范数
| 类别 | 公式 | 含义 |
| 1-范数 | 列元素绝对值之和,取最大 | |
| 2-范数 | ||
| |
对应1-范数,行元素绝对值和最大 | |
| F-范数 | 全部元素平方和开方 |
3.非齐次线性方程组的解
![]()
![]()
因为![]() ,所以
,所以
![]()
若A行满秩,则:
![]()
若A列满秩,则:
![]()
![]()
六、矩阵序列与矩阵函数
1.矩阵函数
设一元函数f(z)能展开为z的幂级数![]()
silu![]() 表示幂级数的收敛半径,当n阶矩阵A的谱半径
表示幂级数的收敛半径,当n阶矩阵A的谱半径![]() 时,将收敛的矩阵幂级数的和
时,将收敛的矩阵幂级数的和![]() 称为矩阵函数,记为
称为矩阵函数,记为
![]()
| z | A |
![]()
![]()
2.矩阵函数求解
1.待定系数法
求解思路:
先求最小特征多项式![]() ,然后设待求矩阵函数为
,然后设待求矩阵函数为![]() ,
,![]() ,其中
,其中![]() 为次数小于
为次数小于![]() 的多项式。然后依次往
的多项式。然后依次往![]() 里面带入特征值
里面带入特征值![]() ,若出现重根,则对
,若出现重根,则对![]() 求导。
求导。
例:
![]()
![]()
![]()
![]()
2.Jordan标准型法
![]()
3.矩阵微分方程
(1)齐次微分方程
![]()
![]()
(2)非齐次微分方程
![]()
![]()
例:
求解微分方程![]() 满足x(0)的解
满足x(0)的解
先求通解:
先求![]()
![]()
![]()
![]()
![]()
x(0)就是c
![]()
再求特解:
合并:
七、矩阵特征值估计
(1)行盖尔圆
每一行除对角线元素外,其他元素绝对值和为第一个盖尔圆半径的边界,圆心为对角线元素
(2)列盖尔圆
列盖尔圆和行盖尔圆原理相同
(3)盖尔圆隔离