算法提高之搜索：DFS之迭代加深、双向dfs、IDA*

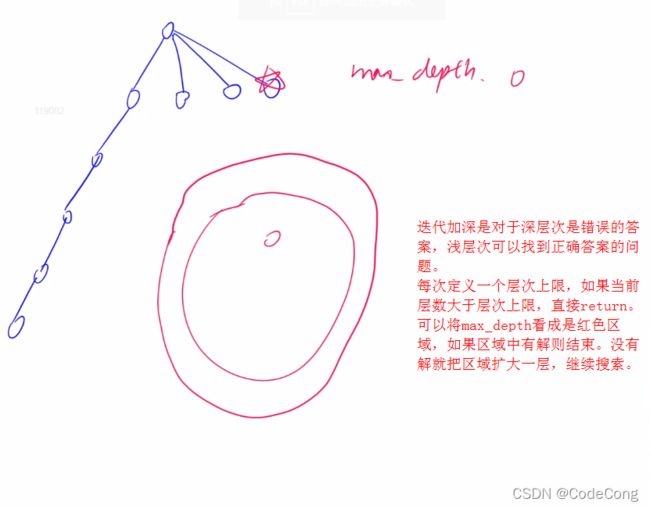
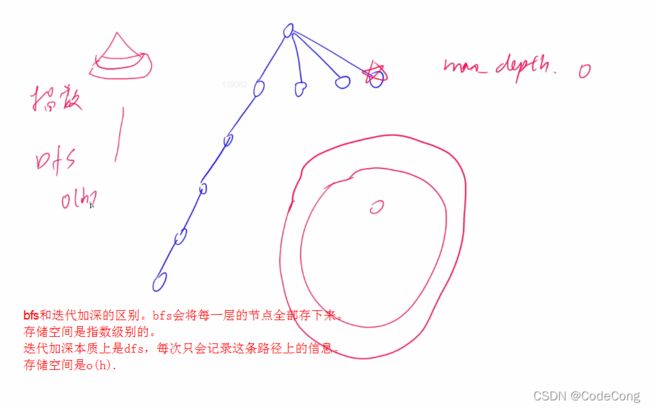
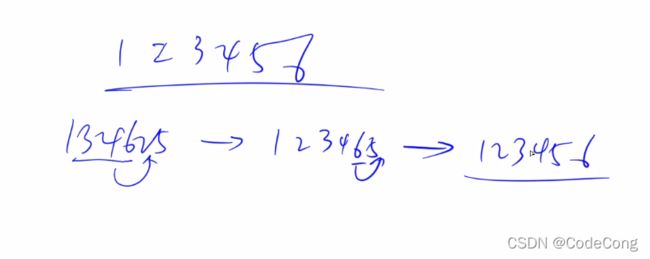1、迭代加深

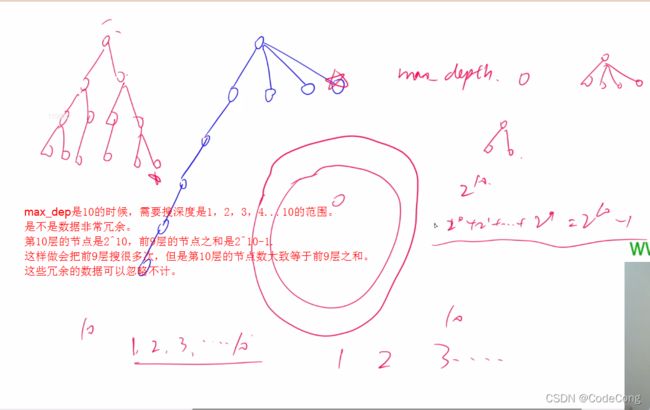
1.1、加成序列

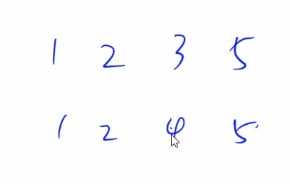
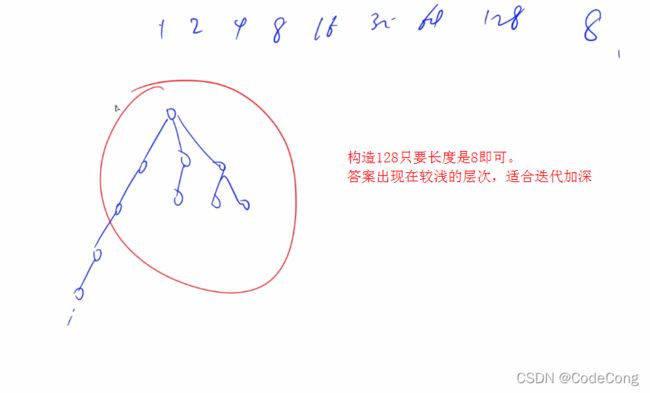
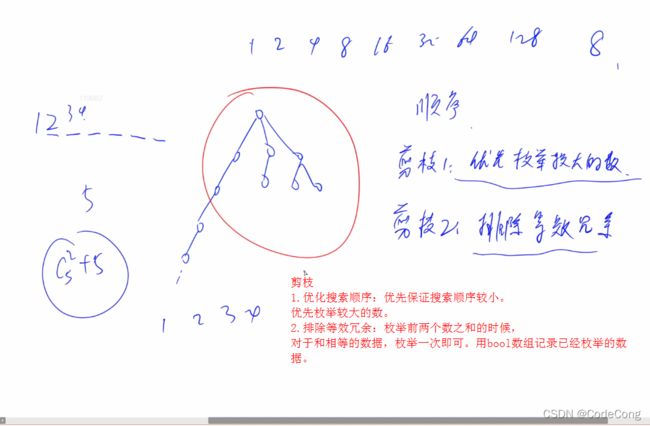
#include 
#include 
#include 

using namespace std;

const int N = 110;

int n;
int path[N];

//当前的层数 最大的层数
bool dfs(int u, int k)
{
    if (u == k) return path[u - 1] == n;
	//判断哪些和用过
    bool st[N] = {0};
    //从大到小枚举 i和j是序列号
    for (int i = u - 1; i >= 0; i -- )
    //选一个组合数即可，规定j从i开始枚举。
        for (int j = i; j >= 0; j -- )
        {
            int s = path[i] + path[j];
            //path[u-1]是最后一个元素，保证path中的数据单调递增
            //大于path[u-1]
            if (s > n || s <= path[u - 1] || st[s]) continue;
            st[s] = true;
            path[u] = s;
            if (dfs(u + 1, k)) return true;
        }

    return false;
}

int main()
{
//第一个数是1.数组从0开始
    path[0] = 1;
    while (cin >> n, n)
    {
    //从小到达枚举迭代加深的范围
        int k = 1;
        //当前深度找不到解 就扩大范围
        while (!dfs(1, k)) k ++ ;
		//答案
        for (int i = 0; i < k; i ++ ) cout << path[i] << ' ';
        cout << endl;
    }

    return 0;
}

2、双向DFS

2.1 送礼物

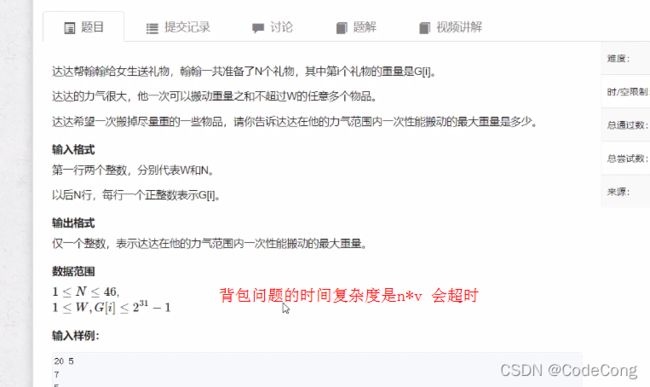
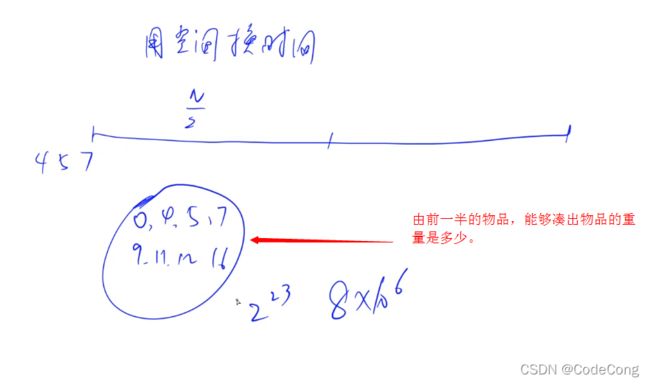
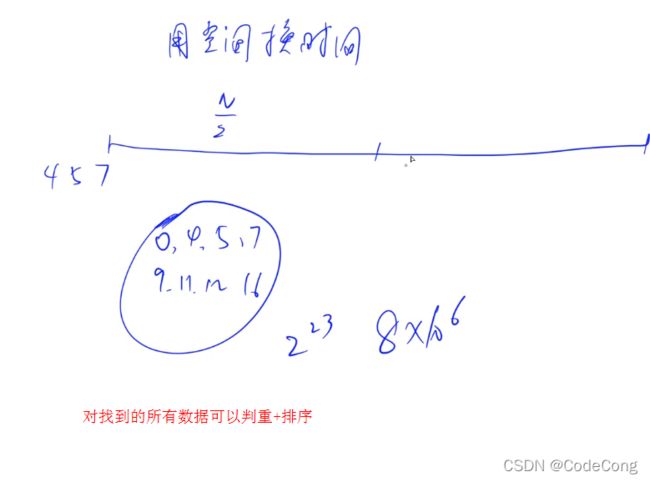
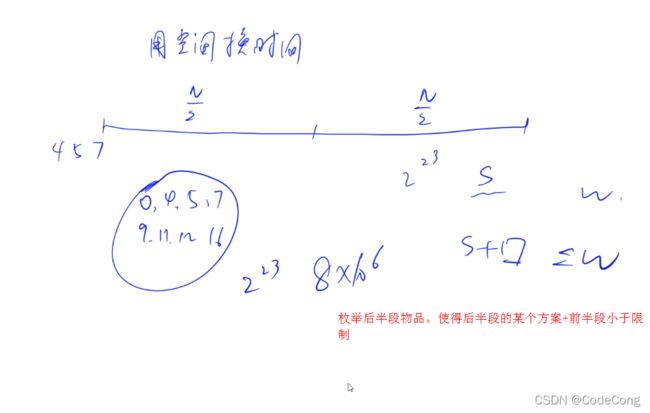
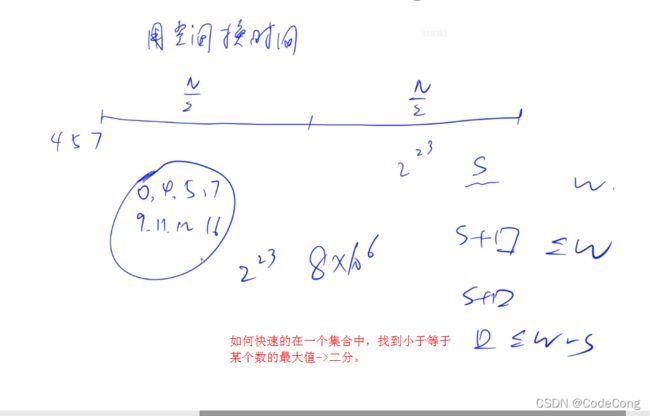
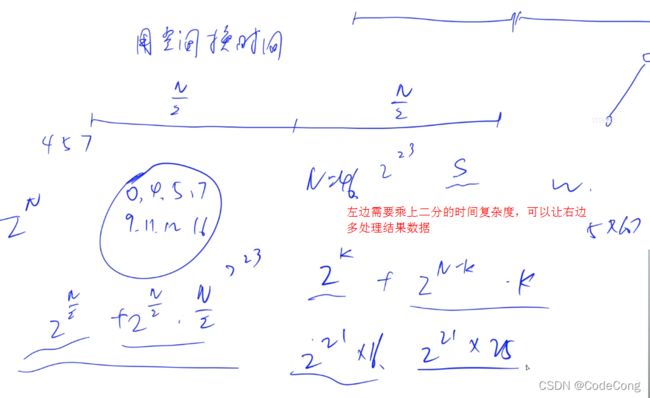
排序的原因是 搜索顺序优化。

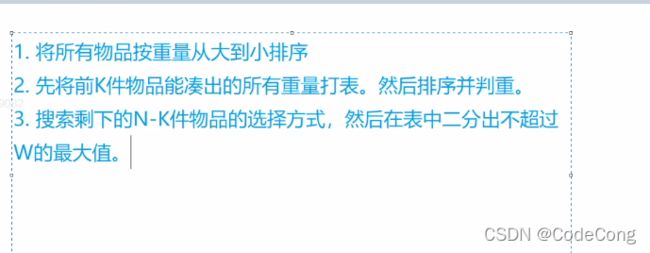
#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 46;
//n是物品个数 m是上限 k表示前半段的物品
int n, m, k;
//原物体的重量
int w[N];
//所有能凑出的物体重量
//  k = n / 2 + 2; k最大=25
int weights[1 << 25], cnt ;
int ans;
//枚举到哪个数  当前的和
void dfs1(int u, int s)
{
    if (u == k)
    {
        weights[cnt ++ ] = s;
        return;
    }
	//当前不选这个物品
    dfs1(u + 1, s);
   	//选这个物品 需要加上可行性剪枝
    if ((LL)s + w[u] <= m) dfs1(u + 1, s + w[u]);
}

void dfs2(int u, int s)
{
    if (u == n)
    {
        int l = 0, r = cnt - 1;
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if ((LL)s + weights[mid] <= m) l = mid;
            else r = mid - 1;
        }
        ans = max(ans, s + weights[l]);
        return;
    }

    dfs2(u + 1, s);
    //每个数最大是2^31，为了防止溢出，转换成LL
    if ((LL)s + w[u] <= m) dfs2(u + 1, s + w[u]);
}

int main()
{
    cin >> m >> n;
    for (int i = 0; i < n; i ++ ) cin >> w[i];
	//优化搜索顺序
    sort(w, w + n);
    reverse(w, w + n);
	//后半段有一个二分，平衡一下前半段。
    k = n / 2 + 2;
    dfs1(0, 0);
	
    sort(weights, weights + cnt);
    //剩下的相互不同的元素个数
    cnt = unique(weights, weights + cnt) - weights;

    dfs2(k, 0);

    cout << ans << endl;

    return 0;
}

3、IDA*

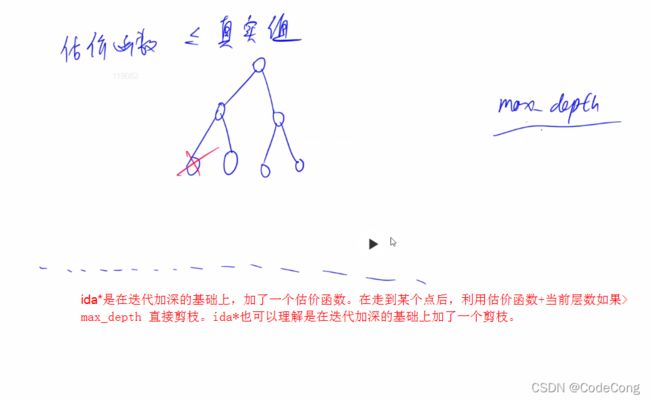
3.1 排书

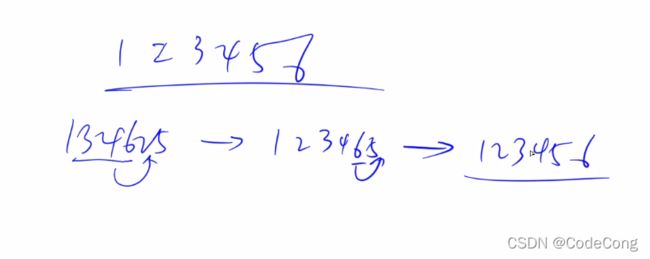
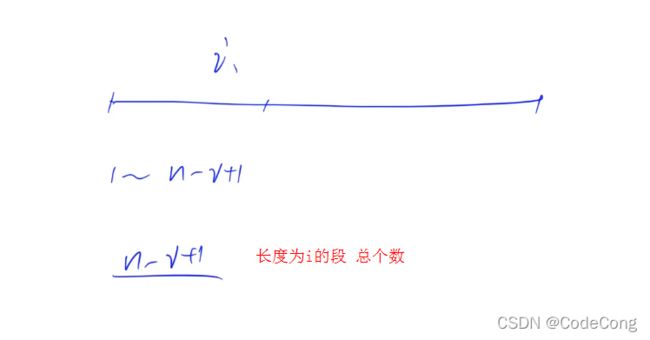
每一次






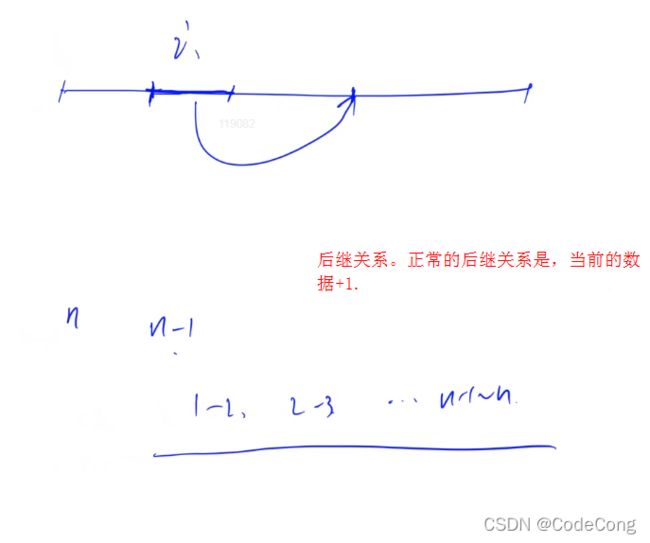
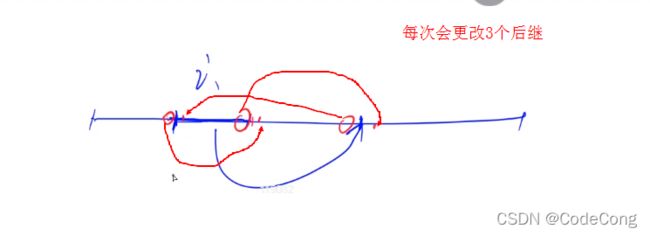
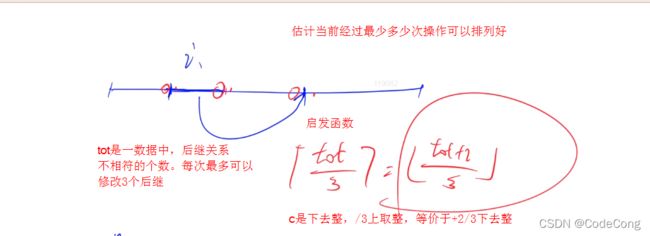
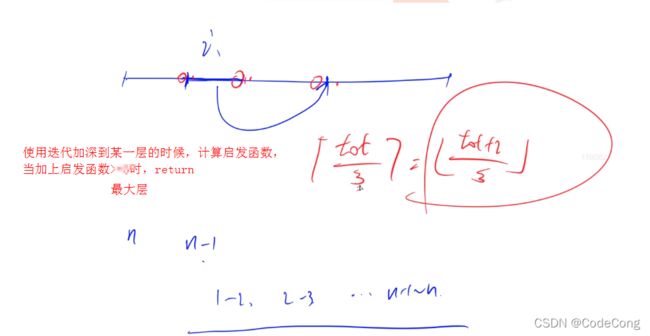
模拟移动书的过程

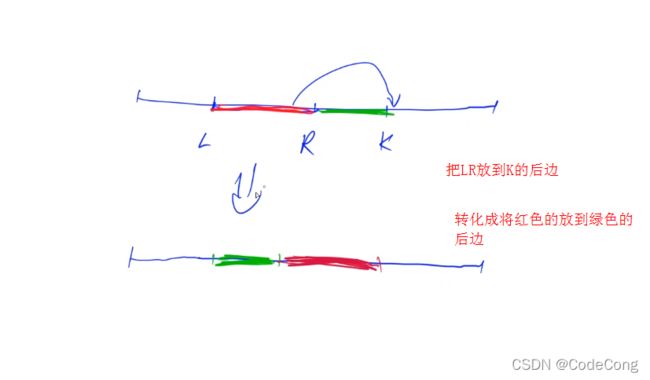
#include 
#include 
#include 
#include 

using namespace std;

const int N = 15;

int n;
int q[N], w[4][N];

int f()
{
    int res = 0;
    for (int i = 0; i + 1 < n; i ++ )
        if (q[i + 1] != q[i] + 1)
            res ++ ;
    return (res + 2) / 3;
}


bool dfs(int depth, int max_depth)
{
    if (depth + f() > max_depth) return false;
    if (f()==0) return true;

    for(int len=1;len<n;len++)
        for(int l=0;l+len-1<n;l++)
         {
            int r=l+len-1;
            for(int k=r+1;k<n;k++)
            {
                memcpy(w[depth], q, sizeof q);
                int x, y;
                //向前放和向后放是一致的，因此只枚举向后放即可。
				//放在r的后面没有意义，放在r+1的后边
                for (x =r+1,y = l; x <= k; x ++, y ++ ) q[y] = w[depth][x];
                for (x = l; x <= r; x ++, y ++ ) q[y] = w[depth][x];
                if (dfs(depth + 1, max_depth)) return true;
                memcpy(q, w[depth], sizeof q);
            }
         }
    return false;
}
 
int main()
{
    int T;
    scanf("%d", &T);
    while (T -- )
    {
        scanf("%d", &n);
        for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

        int depth = 0;
        while (depth < 5 && !dfs(0, depth)) depth ++ ;
        if (depth >= 5) puts("5 or more");
        else printf("%d\n", depth);
    }

    return 0;
}

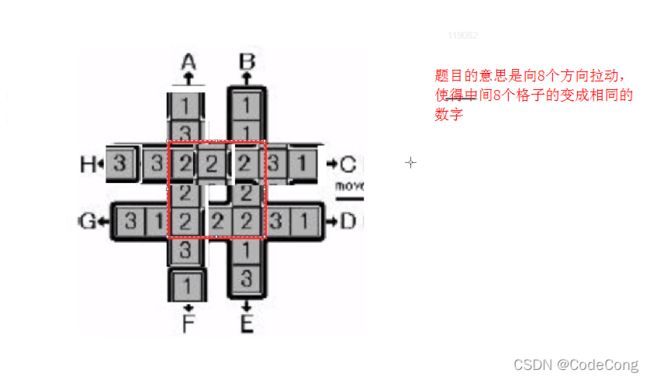
3.2 回转游戏

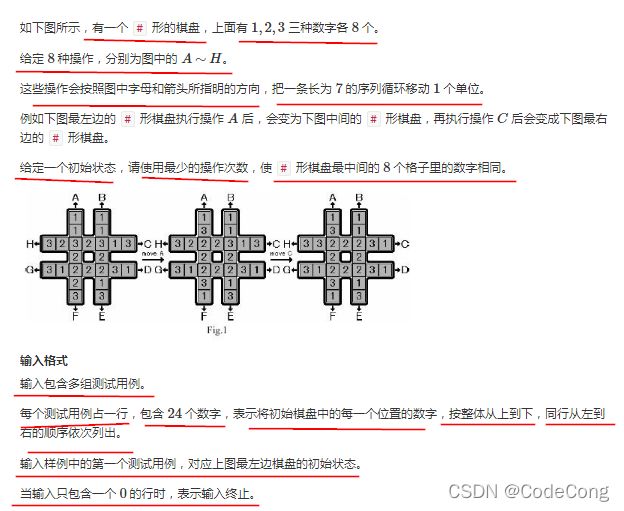
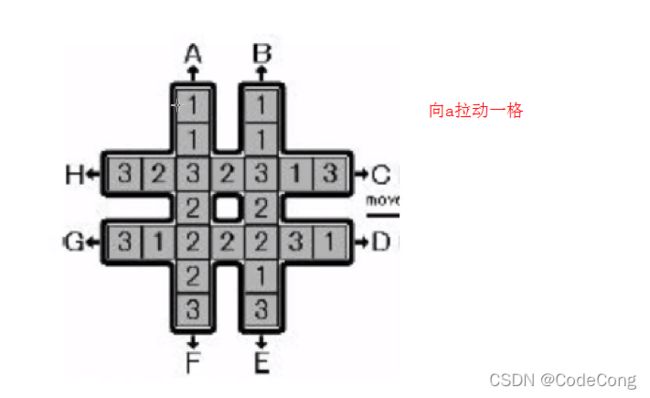
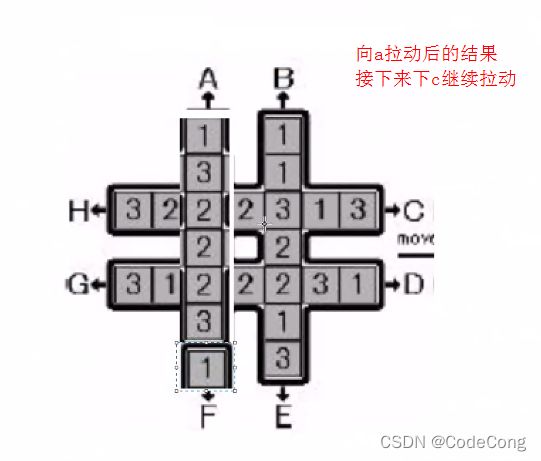
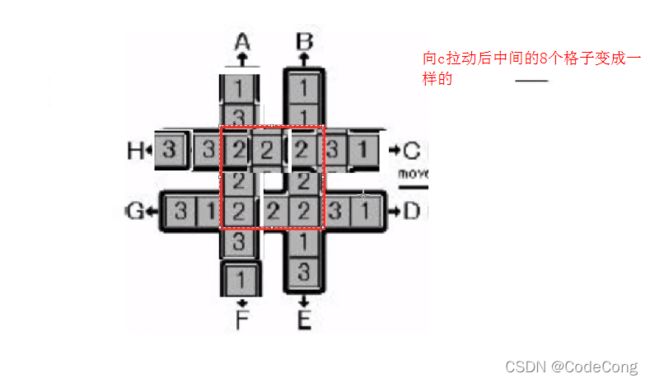
输出字典序最小的操作序列

/*
      0     1
      2     3
4  5  6  7  8  9  10
      11    12
13 14 15 16 17 18 19
      20    21
      22    23
*/

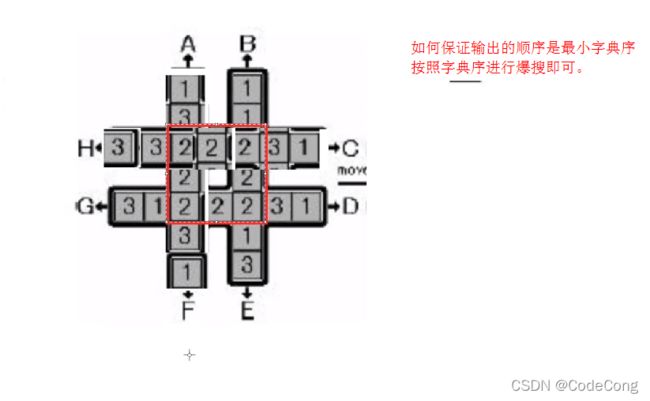
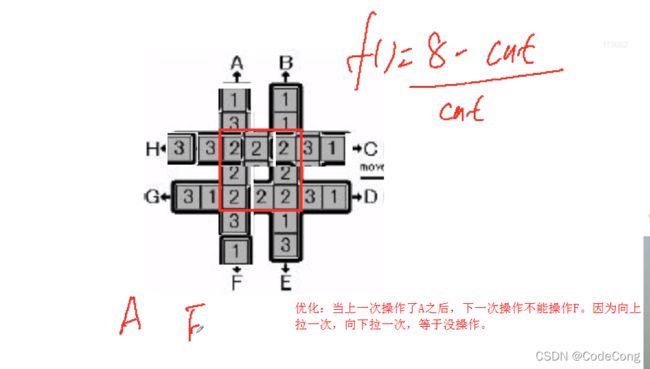
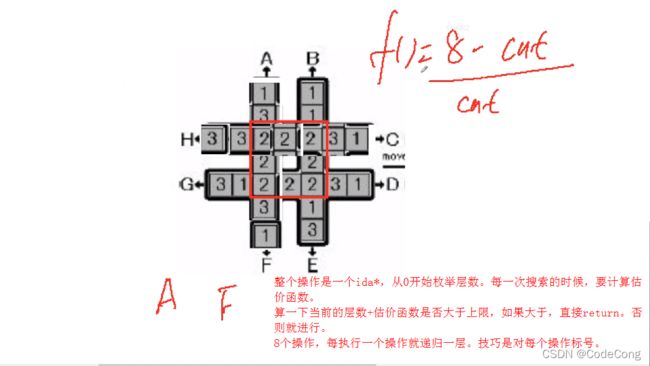
#include 
#include 
#include 

using namespace std;

const int N = 24;
//8个操作分别对应的数据在q中的相对位置
int op[8][7] = {
    {0, 2, 6, 11, 15, 20, 22},
    {1, 3, 8, 12, 17, 21, 23},
    {10, 9, 8, 7, 6, 5, 4},
    {19, 18, 17, 16, 15, 14, 13},
    {23, 21, 17, 12, 8, 3, 1},
    {22, 20, 15, 11, 6, 2, 0},
    {13, 14, 15, 16, 17, 18, 19},
    {4, 5, 6, 7, 8, 9, 10}
};
//记录每一个操作 反向操作的编号
int oppsite[8] = {5, 4, 7, 6, 1, 0, 3, 2};
//记录中间8个数据对应q中数据的相对位置
int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};
//数据
int q[N];
//操作方案 0->A 1->B
int path[100];

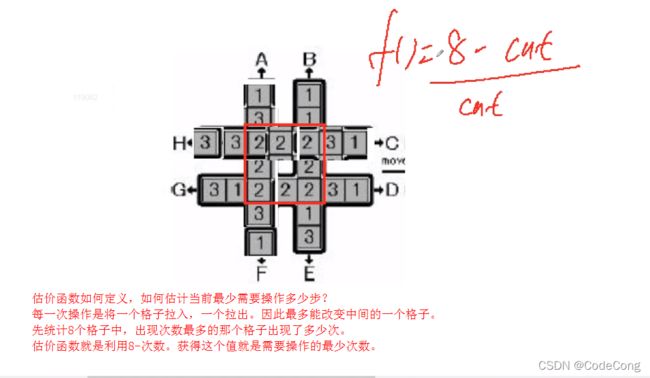
int f()
{
    int sum[4]={0};
    for (int i = 0; i < 8; i ++ ) sum[q[center[i]]] ++ ;

    int maxv = 0;
    for (int i = 1; i <= 3; i ++ ) maxv = max(maxv, sum[i]);

    return 8 - maxv;
}

void operate(int x)
{
    int t = q[op[x][0]];
    for (int i = 0; i < 6; i ++ ) q[op[x][i]] = q[op[x][i + 1]];
    q[op[x][6]] = t;
}

bool dfs(int depth, int max_depth, int last)
{
    if (depth + f() > max_depth) return false;
    if (f() == 0) return true;

    for (int i = 0; i < 8; i ++ )
        if (last != oppsite[i])
        {
            operate(i);
            path[depth] = i;
            if (dfs(depth + 1, max_depth, i)) return true;
            operate(oppsite[i]);
        }

    return false;
}

int main()
{
    while (cin >> q[0], q[0])
    {
        for (int i = 1; i < 24; i ++ ) cin >> q[i];

        int depth = 0;
        // 从0层开始，预计的深度，上一层所进行的操作。
        //最后一个参数是优化 在本次操作中不进行与上一层操作相反的操作。
        while (!dfs(0, depth, -1)) depth ++ ;
		//深度为0
        if (!depth) printf("No moves needed");
        else
        {
            for (int i = 0; i < depth; i ++ ) printf("%c", 'A' + path[i]);
        }
        //输出中间的数据  q[6]就是中间的数据
        printf("\n%d\n", q[6]);
    }

    return 0;
}