蓝桥杯AcWing学习笔记 2-1二分的学习(附相关蓝桥真题:四平方和、分巧克力)(Java)
有参加蓝桥杯的同学可以给博主点个关注,博主也在准备蓝桥杯,可以跟着博主的博客一起刷题。
蓝桥杯
我的AcWing
题目及图片来自蓝桥杯C++ AB组辅导课
二分
二分看似是一个很简单的算法,但我们在写的时候可能会遇到各种各样的问题,尤其是二分的一些边界问题,我们怎么取边界是一个很重要的问题。
思想:
- 确定一个区间[L, R],使得目标值一定在区间中
- 找一个性质,满足:
① 性质具有二段性
② 答案是二段性的分界点
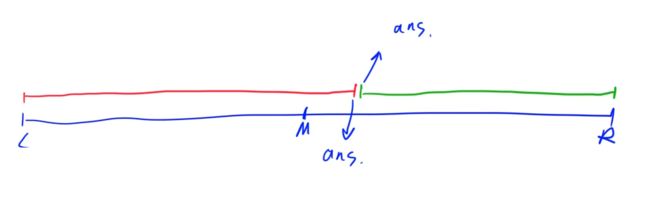
整数二分的模板分为两大类,一种答案是红色区间的右端点,另一种答案是绿色区间的左端点,这是不一样的两个问题。
假设当前区间为LR,中点为M。
第一类(ans是红色区间的右端点):将[L, R]分为[L, M - 1],[M, R]。
if M是红色的,说明答案必然在[M, R]之间;
else M是绿色的,说明答案必然在[L, M - 1]之间。
伪代码模板:
while (L < R) {
int M = (L + R + 1) / 2; // 由于整数要下取整,所以要补上1
if (M为红色) L = M;
else R = M - 1;
}
第二类(ans是绿色区间的左端点):将[L, R]分为[L, M],[M + 1, R]。
if M是绿色的,说明答案必然在[L, M]之间;
else 说明答案必然在[M + 1, R]之间。
伪代码模板:
while (L < R) {
int M = (L + R) / 2;
if (M为绿色) R = M;
else L = M + 1;
}
我们做题的时候不需要判断这个二分属于第一类还是第二类,我们只需要关注代码里写的是L = M还是R = M,注意如果是L = M一定要注意L + R + 1,这样就不会出现死循环。
整数二分步骤:
- 找一个区间[L,R],使得答案一定在该区间中
- 找一个判断条件,使得该判断条件具有二段性,并且答案一定是该二段性的分界点。
- 分析中点M在该判断条件下是否成立,如果成立,考虑答案在哪个区间;如果不成立,考虑答案在哪个区间;
- 如果更新方式写的是R(右) = Mid,则不用做任何处理;如果更新方式写的是L(左)= Mid,则需要在计算Mid时加上1。
按照上方步骤写代码就可以完美避开整数二分所有的坑。
实数二分
实数二分相对与整数二分就非常简单了,因为我们的M必然是区间的中点,因为实数是稠密的,我们考虑的时候就不需要考虑中点是属于左边还是右边了,直接将区间[L, R]划分成[L, M],[M, R]。
整数二分循环停止的条件是当区间里只有一个数,否则继续二分;
实数二分是当我们的区间长度足够小的时候就停止,一般写成while (R - L > 1e-6)。
if ans在[M, R] L = M;
else ans在[L, M] R = M;
伪代码模板:
while (R - L > 1e-6) {
double M = (L + R) / 2;
if (ans在[M, R]) L = M;
else R = M;
}
例题
AcWing 789. 数的范围
整数二分
最经典的二分题。
这题是求数的起始位置和终止位置,所以一个数必然有它的左端点和右端点,如果这个数在数组中只有一个,那么它的左端点和右端点是重合的。
数组长度为n,区间范围:[0, n - 1]。
我们先来找左端点,我们可以用一个什么样的二段性,把这个左端点变成二段性的分界点呢?
假设我们要找的数为x,那么我们的左端点一定是大于等于x的第一个位置;
判断条件可以设为:q[mid] >= x。
最后还需要判断一下,如果q[r] == x,说明x在数组中存在,输出r就是x的左端点,也就是x的起始位置。
那么右端点怎么二分呢?
先找区间的范围,我们还是可以用[0, n - 1],但我们已经找到二分的左端点了,不妨写成[左端点, n - 1]。
判断条件可以设为:q[mid] <= x。
import java.util.Scanner;
public class Main {
static int n, m;
static final int N = 100010;
static int[] q = new int[N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for (int i = 0; i < n; i++) q[i] = sc.nextInt();
for (int i = 0; i < m; i++) {
int x = sc.nextInt();
int l = 0, r = n - 1; // 确定区间
// 二分求x的左端点
while (l < r) {
int mid = (l + r) / 2;
if (q[mid] >= x) r = mid;
else l = mid + 1;
}
if (q[r] == x) {
System.out.print(r + " ");
// 二分求x的右端点
r = n - 1;
while (l < r) {
int mid = (l + r + 1) / 2; // 因为写的是l = mid,所以需要补上1
if (q[mid] <= x) l = mid;
else r = mid - 1;
}
System.out.println(l + " ");
} else {
System.out.println("-1 -1");
}
}
}
}
AcWing 790. 数的三次方根
实数二分
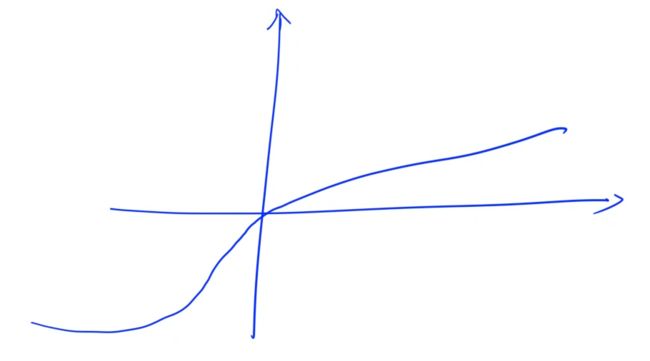
三次方根函数图像大概如下图:
函数是有单调性的,有单调性一定可以二分,能二分不一定有单调性。
区间就可以取本题的数据范围[−10000, 10000]。
此题比较简单,直接套模板即可。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
double n = sc.nextDouble();
double l = -10000, r = 10000;
while (r - l > 1e-8) { // 模板是1e-6,但保证我们的精度足够,要比我们输出的小数点多取两位,也就是1e-8
double mid = (l + r) / 2;
if (mid * mid * mid >= n) r = mid;
else l = mid;
}
System.out.print(String.format("%.6f", l)); // 取6位小数
}
}
第七届2016年蓝桥杯真题
AcWing 1221.四平方和
JavaB组第8题
四个数a b c d,输出字典序最小的表示
蓝桥杯的话,用三层循环暴搜也是可以拿满分的,但y总在AcWing加强了数据,会卡掉 O ( N 3 ) O(N^3) O(N3)的暴力算法,所以本文讲的是y总的二分优化代码(y总Orz)。
先考虑我们的时间复杂度,由于 N ⩽ 5 × 1 0 6 N \leqslant5×10^6 N⩽5×106,每个数都是以平方形式表示的,所以每个数的范围: x x x ⩽ N \leqslant\sqrt{N} ⩽N,大概就是 x ⩽ 2200 x \leqslant 2200 x⩽2200,判断我们最多能枚举几个数,如果枚举三个数的话,就是 220 0 3 2200^3 22003,大概是 8 × 1 0 9 8×10^9 8×109,就会超时,所以我们最多只能枚举两个数。
但本题是有四个数的,其实枚举三次就可以,最后一个数可以通过数学知识推出来。
本来我们应该枚举三重for循环:
for (a...) {
for (b...) {
for (c...){
...
}
}
}
但我们可以用空间换时间,先枚举一半,把这一半的数据存下来,我们先枚举c和d:
for (c = 0; c² <= N; c++) {
for (d = c; c² + d² <= N; d++) { // d = c剪枝优化
把c² + d²存起来
}
}
将数据存起来的时间复杂度是 O ( N ² ) O(N²) O(N²),没超,存完之后我们可以枚举a和b:
for (a = 0; a² <= N; a++) {
for (b = a; b² + a² <= N; b++) {
t = n - a² + b²; // 计算和最终答案还差多少
if t在前面c² + d²出现过,那就说明我们找到了一组解
}
}
我们的时间复杂度大概是:
快速判断某一个数是否在一堆数中出现过,我们可以用哈希或者二分,我们把这一步原先的 O ( N ) O(N) O(N)优化成了 O ( 1 ) O(1) O(1)或者是 O ( l o g n ) O(logn) O(logn)。
但我们还需要找到字典序最小的解,我们枚举完之后,a和b一定是能保证最小的,我们只需要找到c和d同时最小的一个解,也就是说我们在存方案的时候,除了找到t是否出现过,同时还要找到t字典序最小的一个组合,排序的时候要排三个数:c² + d²、c、d,按照字典序排这三个数的组合即可。
排完之后我们二分找t的时候,只要找到大于等于n - a² + b²的字典序最小的一个数就可以了。
其实这个题与带分数的转换方法类似, a ² + b ² + c ² + d ² = n a² + b² + c² + d² = n a²+b²+c²+d²=n可以转换成 c ² + d ² = n − a ² − b ² c² + d² = n − a² − b² c²+d²=n−a²−b²(这篇文章讲了带分数)
二分代码
时间复杂度 O ( N 2 l o g N ) O(N^2logN) O(N2logN)
用类存值(AcWing超时,蓝桥杯满分)
这个代码就是y总的Java版代码,但这题数据卡的太死了,超时了,但在蓝桥杯是可以满分的,就是时间有点要爆。
import java.util.Scanner;
import java.util.Arrays;
class Sum implements Comparable<Sum> {
int s, c, d; // s是c² + d²
public Sum(int s, int c, int d) {
this.s = s;
this.c = c;
this.d = d;
}
// 比较器作用:返回字典序最小的值
@Override
public int compareTo(Sum t) {
if (s != t.s) return Integer.compare(s, t.s);
if (c != t.c) return Integer.compare(c, t.c);
return Integer.compare(d, t.d);
}
}
public class Main {
static final int N = 2500010;
static int n, m;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Sum[] sum = new Sum[N];
n = sc.nextInt();
for (int c = 0; c * c <= n; c++) {
for (int d = c; c * c + d * d <= n; d++) {
sum[m++] = new Sum(c * c + d * d, c, d);
}
}
Arrays.sort(sum, 0, m); // 排序前m个数
for (int a = 0; a * a <= n; a++) {
for (int b = a; a * a + b * b <= n; b++) {
int t = n - a * a - b * b;
int l = 0, r = m - 1;
while (l < r) {
int mid = (l + r) / 2;
if (sum[mid].s >= t) r = mid;
else l = mid + 1;
}
if (sum[l].s == t) {
System.out.println(a + " " + b + " " + sum[l].c + " " + sum[l].d);
return ;
}
}
}
}
}
用集合存值(AcWing通过,蓝桥杯满分)
这个是用List集合存数据,然后在主类里面重写集合排序方法的比较器,AcWing是可以过的。
我认为上一个代码没过的原因是我在Sum类里重写了比较器,然后在主类又用了Arrays.sort()方法,导致超时了,应该跟用类存取值或者集合存取值没有关系,如果有大佬知道原因的话,希望可以指明。
import java.util.Scanner;
import java.util.ArrayList;
class Sum {
int s, c, d; // s是c² + d²
public Sum(int s, int c, int d) {
this.s = s;
this.c = c;
this.d = d;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
ArrayList<Sum> sum = new ArrayList<>();
int n = sc.nextInt();
for (int c = 0; c * c <= n; c++) {
for (int d = c; c * c + d * d <= n; d++) {
sum.add(new Sum(c * c + d * d, c, d));
}
}
sum.sort((o1,o2)->{
if (o1.s != o2.s) return o1.s - o2.s;
if (o1.c != o2.c) return o1.c - o2.c;
return o1.d - o2.d;
});
for (int a = 0; a * a <= n; a++) {
for (int b = a; a * a + b * b <= n; b++) {
int t = n - a * a - b * b;
int l = 0, r = sum.size() - 1;
while (l < r) {
int mid = (l + r) / 2;
if (sum.get(mid).s >= t) r = mid;
else l = mid + 1;
}
if (sum.get(l).s == t) {
System.out.println(a + " " + b + " " + sum.get(l).c + " " + sum.get(l).d);
return ;
}
}
}
}
}
三层循环暴搜(AcWing超时,蓝桥杯满分)
时间复杂度 O ( N 3 ) O(N^3) O(N3)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int a = 0; a * a <= n; a++) {
for (int b = a; a * a + b * b <= n; b++) {
for (int c = b; a * a + b * b + c * c <= n; c++) {
int t = n - a * a - b * b - c * c;
int d = (int)Math.sqrt(t);
if (d * d == t) {
System.out.print(a + " " + b + " " + c + " " + d);
return ;
}
}
}
}
}
}
看一下三个代码在蓝桥杯系统中的评测结果:
可以看出在蓝桥杯的数据中,暴搜是最快的,为什么我们的优化反而不如暴搜呢?可以多用几个数来做测试,发现a和b的值从来就没有超过10,所以说明a和b循环的次数非常少,所以y总加强了这个题的数据,AcWing中只有第二种用集合存值是可以过的,y总主要是想体现本题的二分思想。
第八届2017年蓝桥杯真题
AcWing 1227. 分巧克力
JavaB组第9题
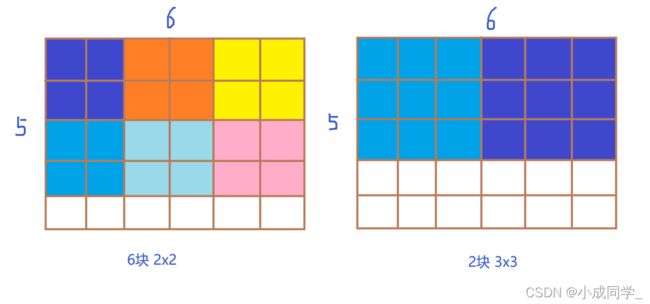
将N块长方形的巧克力均匀分成K块边长最大的正方形巧克力 不可以拼接
例如一块6×5的巧克力可以切出6块2×2的巧克力或者2块3×3的巧克力:
我们先想想这个题用二分怎么来做。
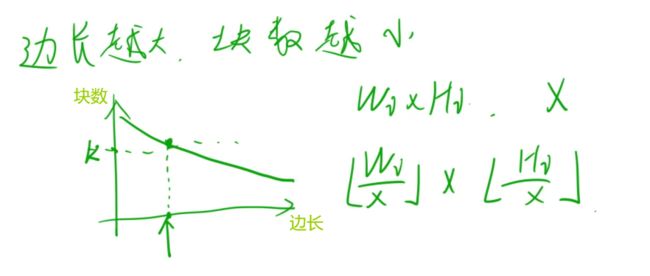
边长越大,块数越少,我们看一下函数曲线:
我们要找到一个满足块数大于等于K的,最大的一个边长,所有小于等于这个点的一定可以切出来K块,这就是我们二分的关键。
二分的判断条件:f(x) >= K,f(x)返回的是块数,找到满足这个性质最大的x。
if (f(mid) >= K),说明所有小于等于mid的值都满足要求,所以更新:l = mid。
时间复杂度 O ( N l o g H ) O(NlogH) O(NlogH);可能是H或者W。
import java.util.Scanner;
public class Main {
static final int N = 100010;
static int n, k;
static int[] h = new int[N];
static int[] w = new int[N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
k = sc.nextInt();
for (int i = 0; i < n; i++) {
h[i] = sc.nextInt();
w[i] = sc.nextInt();
}
int l = 1, r = 100000; // 至少能获得一块 1×1 的巧克力,区间为[1, 1e5]
while (l < r) {
int mid = l + r + 1 >> 1; // 右移1位跟/2同理,这里要+1
if (check(mid)) l = mid;
else r = mid - 1;
}
System.out.print(l);
}
private static boolean check(int mid) {
int res = 0;
for (int i = 0; i < n; i++) {
res += (h[i] / mid) * (w[i] / mid); // 图中的公式
if (res >= k) return true;
}
return false;
}
}
有对代码不理解的地方可以在下方评论