C++是如何从代码到游戏的

连连看游戏规则：只要将相同的两张牌用三根以内的直线连在一起就可以消除，规则简单容易上手。游戏速度节奏快，画面清晰可爱，适合细心的玩家。        

C++是如何从代码到游戏的中非常有趣的讲述了从代码到游戏的过程，在整体结构上，描述的非常棒粉丝留言是这样调侃的传说中的先画个大体线条，然后填充亿点点细节，然后就简单的完成了

这不亚于告诉你飞机长啥样，然后让你去造飞机，要知道，就是那亿点点细节让很多人望而止步，逻辑之难，难于上青天。

没关系，本期带你看那亿点点细节

正文

游戏设计

「整体结构」

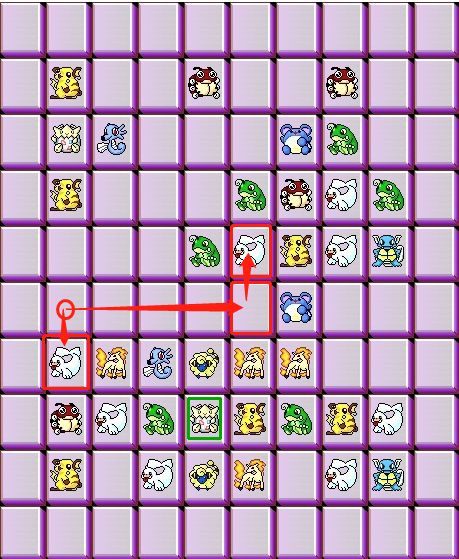
首先呢是红色包围的整个地图，外圈辅助，说白了就是一个10*10数组，外圈为0.

整体结构肯定都晓得，游戏设计就看怎么消除相同的图片 消除相同的图片分三种情况

0个转折点

就是点击的两张图片在一条直线上，并且中间没有障碍物才可以通行

1个转折点

点击的两张图片不在一条直线上，那么这两张图片可能存在的转折点有两个，在对角区域

2个转折点

这个就比较复杂，两个转折点可能的情况太多，只能枚举出来，然后循环判断

「有没有什么好点的办法」

我们可以先确定一个转折点，将这个转折点当成点击的图片，去和另一张图片匹配，这样我们就可以用判断「1个转折点」的方法+判断「0个转折点」的方法,来实现「两个转折点」复杂的情况，「这个时候只需要罗列出其中一个转折点可能出现的地方就行了」

在一个转折点的判断里面用的就是0个转折点的方法

游戏三部曲

  InitGame();  //初始化游戏
  while (1)
  {
    UpdateGame();//数据更新
    DrawGame();  //绘制游戏
  }

「Easyx制作游戏，三部曲整起」

初始化游戏

全局定义地图大小

#define MAP_ROW 10	
#define MAP_COL 10
#define MAP_SIZE ( MAP_ROW - 2 ) * ( MAP_COL - 2 )	//地图大小

初始时给地图赋值

/*初始化变量*/
int tempMap[MAP_SIZE] = { 0 };
/*随机生成地图数据*/
for (int i = 0; i < MAP_SIZE / 2; i++)
{
	tempMap[i] = rand() % g_randSize + 1;       /*随机[1 - 10]*/
	tempMap[MAP_SIZE / 2 + i] = tempMap[i];
}
/*打乱数据*/
for (int i = 0; i < MAP_SIZE; i++)
{
	int index = rand() % MAP_SIZE;
	if (index != i)
	{
		int temp = tempMap[i];
		tempMap[i] = tempMap[index];
		tempMap[index] = temp;
	}
}
/*转成一个二维地图数组*/
int index = 0;
for (int i = 0; i < MAP_ROW; i++)
{
	for (int j = 0; j < MAP_COL; j++)
	{
		if (i == 0 || i == MAP_ROW - 1 || j == 0 || j == MAP_COL - 1)
		{
			g_map[i][j] = 0;
		}
		else
		{
			g_map[i][j] = tempMap[index++];
		}
	}
}

「因为图片要两两配对，只能先用一维数组赋值，再转成二维数组储存」

绘制游戏

这里是将图片资源贴在地图指定的地方，不同的框架绘制的方法不一，但都大体相同，双缓冲处理闪屏问题，绘制的界面好看与否取决于GUI，这里比较low，暂且这样

BeginBatchDraw();
/*绘制方块*/
for (int i = 0; i < MAP_ROW; i++)
{
	for (int j = 0; j < MAP_COL; j++)
	{
		putimage(j * 46, i * 56, 46, 56, &g_block, 0, 56, SRCCOPY);
	}
}
/*绘制动物*/
for (int i = 1; i < MAP_ROW - 1; i++)
{
	for (int j = 1; j < MAP_COL - 1; j++)
	{
		/*不等于0，绘制动物，等于0，什么都不绘制 动物图片大小为39 * 39 */
		if (g_map[i][j] != 0)
		{
			putimage(j * 46 + 1.5, i * 56 + 6, 39, 39, &g_animal, 39, (g_map[i][j] - 1) * 39, SRCAND);
			putimage(j * 46 + 1.5, i * 56 + 6, 39, 39, &g_animal, 0, (g_map[i][j] - 1) * 39, SRCPAINT);
		}
	}
}
setlinecolor(GREEN);  //设置线条颜色
setlinestyle(PS_SOLID | PS_ENDCAP_FLAT, 3);	//画线样式为宽度 3 像素的实线，端点为平坦的
if (g_clickIndex > 0)
{
	rectangle(g_targetPos[0].X * 46 + 4, g_targetPos[0].Y * 56 + 4, g_targetPos[0].X * 46 + 36, g_targetPos[0].Y * 56 + 44);
}
EndBatchDraw();

数据更新

「在数据更新之前，先定义好两个位置变量存储鼠标点击位置」

int    g_clickIndex = 0;			//点击的下标
COORD  g_targetPos[2] = { -1, -1 };	//点击的两个位置

数据更新时获取鼠标点击的位置转化为地图坐标

MOUSEMSG msg = GetMouseMsg();
int row = msg.y / 56;
int col = msg.x / 45;
switch (msg.uMsg)		/*msg.uMsg得到一个鼠标消息*/
{
case WM_LBUTTONDOWN:    /*鼠标左键按下*/
	g_targetPos[g_clickIndex].X = col;    /*下标：0，1，超出了就越界*/
	g_targetPos[g_clickIndex].Y = row;
	break;

这个时候你就拥有了玩家点击两张图片在地图上的位置

对图片进行消除

/*点击一张图片两下，不消除，直接返回*/
if (g_targetPos[0].X == g_targetPos[1].X && g_targetPos[0].Y == g_targetPos[1].Y)
	return;
/*点击两张图片，判断鼠标两个坐标的位置值不相等，直接返回*/
if (g_map[g_targetPos[0].Y][g_targetPos[0].X] != g_map[g_targetPos[1].Y][g_targetPos[1].X])
{
	return;
}

/*进行消除操作*/
if (HavePath(g_targetPos) == true)
{
	for (int i = 0; i < 2; i++)
	{
		g_map[g_targetPos[i].Y][g_targetPos[i].X] = 0;
	}
	g_score -= 2;
}

g_targetPos[0]和g_targetPos[1]是玩家点击两张图片的位置，先判断「点击的是不是同一张图片」，再判断「点击的图片在地图中的值是否相同」,也就是玩家眼中图片是否相同

调用消除函数HavePath(g_targetPos)

「消除函数的原型我是这样定义的」

bool HavePath(COORD targetPos[]);
bool HavePathCorner0(COORD p1, COORD p2);	//没有转折点
bool HavePathCorner1(COORD p1, COORD p2);	//一个转折点
bool HavePathCorner2(COORD p1, COORD p2);	//两个转折点

顺便把0个、1个、2个转折点的函数原型也列举出来

我们看下「消除函数」

bool HavePath(COORD targetPos[])
{
	/*没有转折点*/
	if (HavePathCorner0(targetPos[0], targetPos[1]) == true)
	{
		returntrue;
	}
	/*有一个转折点*/
	if (HavePathCorner1(targetPos[0], targetPos[1]) == true)
	{
		returntrue;
	}
	/*有两个转折点*/
	if (HavePathCorner2(targetPos[0], targetPos[1]) == true)
	{
		returntrue;
	}
	returnfalse;
}

好像串起来了，数据更新里面把坐标传给HavePath函数，HavePath函数判断传入的坐标对应的图片到底有可不可以消除，可以消除就返回true,不可以false.然后分别讨论每个情况，是一个转折点还是几个转折点。

「看起来是不是变简单了」

我么接着往下看

0个转折点

bool HavePathCorner0(COORD p1, COORD p2)
{
	/*判断两张图片是否在一条直线上，不是，直接返回false*/
	if (p1.X != p2.X && p2.Y != p1.Y)
		returnfalse;
	/*为什么求最大值，最小值
	  因为：给的参数，不清楚你的p1,p2的坐标谁最大*/
	  
	int min = 0, max = 0;
	/*竖向：判断竖向是否都为空*/
	if (p1.X == p2.X)
	{
		min = p1.Y < p2.Y ? p1.Y : p2.Y;
		max = p1.Y > p2.Y ? p1.Y : p2.Y;
		for (min++; min < max; min++)
		{
			if (g_map[min][p1.X] != 0)
				returnfalse;
		}
	}

	/*横向：判断横向是否都为空*/
	if (p1.Y == p2.Y)
	{
		min = p1.X < p2.X ? p1.X : p2.X;
		max = p1.X > p2.X ? p1.X : p2.X;
		for (min++; min < max; min++)
		{
			if (g_map[p1.Y][min] != 0)
				returnfalse;
		}
	}
	returntrue;
}

看起来挺复杂的，其实就是「横向纵向判断」（你不晓得两个点是横向还是纵向），从某一点到某一点是否有障碍物,有返回false,没有继续判断，所有判断完成之后返回true,说明两点之间没有障碍物。

1个转折点

bool HavePathCorner1(COORD p1, COORD p2)
{
	//找到转折点
	COORD temp[2];	//两个目标是转折点
	temp[0].X = p1.X;
	temp[0].Y = p2.Y;
	temp[1].X = p2.X;
	temp[1].Y = p1.Y;
	//判断第一个转折点是否连通
	if (g_map[temp[0].Y][temp[0].X] == 0)
	{
		if (HavePathCorner0(p1, temp[0]) == true && HavePathCorner0(p2, temp[0]) == true)
		{
			line(p1.X * 46 + 23, p1.Y * 56 + 28, temp[0].X * 46 + 23, temp[0].Y * 56 + 28);
			line(p2.X * 46 + 23, p2.Y * 56 + 28, temp[0].X * 46 + 23, temp[0].Y * 56 + 28);
			returntrue;
		}
	}
	//判断第二个转折点是否连通
	if (g_map[temp[1].Y][temp[1].X] == 0)
	{
		if (HavePathCorner0(p1, temp[1]) == true && HavePathCorner0(p2, temp[1]) == true)
		{
			line(p1.X * 46 + 23, p1.Y * 56 + 28, temp[1].X * 46 + 23, temp[1].Y * 56 + 28);
			line(p2.X * 46 + 23, p2.Y * 56 + 28, temp[1].X * 46 + 23, temp[1].Y * 56 + 28);
			returntrue;
		}
	}
	returnfalse;
}

先把转折点（对角点）所在的地方定义好，然后先「判断转折点是否是障碍物」，不是的话就可以「调用0个转折点」判断转折点和图片位置是否连通

 

「好嘛，一个调用一个，一套一套的」

2个转折点

「两个转折」点是以「一个转折点」为基础构建「0个转折点」和「1个转折点」的方法，让程序变得简单，看下代码：

bool HavePathCorner2(COORD p1, COORD p2)
{
	COORD temp;

	//任取一目标，往上找
	for (temp.Y = p1.Y - 1, temp.X = p1.X; temp.Y >= 0; temp.Y--)
	{
		//如果往上找直到找到不为空的就结束，或者找到顶了
		if (g_map[temp.Y][temp.X] != 0)
			break;
		//可以判断temp点到p1点是一路为空的，只需要判断p2点和temp是否为只有一个转折点就可以
		if (HavePathCorner1(p2, temp))
			returntrue;
	}
	//任取一目标，往下找
	for (temp.Y = p1.Y + 1, temp.X = p1.X; temp.Y < MAP_ROW; temp.Y++)
	{
		//如果往下找直到找到不为空的就结束，或者找到顶了
		if (g_map[temp.Y][temp.X] != 0)
			break;
		//可以判断temp点到p1点是一路为空的，只需要判断p2点和temp是否为只有一个转折点就可以
		if (HavePathCorner1(p2, temp))
			returntrue;
	}

	//任取一目标，往左找
	for (temp.X = p1.X - 1, temp.Y = p1.Y; temp.X >= 0; temp.X--)
	{
		//如果往左找直到找到不为空的就结束，或者找到顶了
		if (g_map[temp.Y][temp.X] != 0)
			break;
		//可以判断temp点到p1点是一路为空的，只需要判断p2点和temp是否为只有一个转折点就可以
		if (HavePathCorner1(p2, temp))
		  returntrue;
	}
	//任取一目标，往右找
	for (temp.X = p1.X + 1, temp.Y = p1.Y; temp.X < MAP_COL; temp.X++)
	{
		//如果往下找直到找到不为空的就结束，或者找到顶了
		if (g_map[temp.Y][temp.X] != 0)
			break;
		//可以判断temp点到p1点是一路为空的，只需要判断p2点和temp是否为只有一个转折点就可以
		if (HavePathCorner1(p2, temp))
			returntrue;
	}

	returnfalse;
}

这个是看着复杂，其实就是上下左右四个方向都遍历一遍，for循环遍历，找可能存在的转折点，怎么判断？，将另「外一个图片点」和这个「转折点」做1个转折点判断

「就这样，大功告成，连连看游戏想想也不难嘛，都是一套接一套，思路搞清楚了，代码是事？」