MindBigData脑电信号数据处理by小波变换（附代码）

前言

MindBigData是公开的脑电信号数据集之一，本文会使用python语言提取其中的数据，使用小波变换进行去噪，最后使用支持向量机进行粗糙分类。因为在CSDN上尚未检索到该数据库的详细介绍和使用方法，所以本文着重介绍这些和展示相关代码。

MindBigData数据库

MindBigData是一个开放的数据集，这是它的访问入口，包含1,207,293个脑电信号，每个脑电信号维持两秒钟。采集的设备是商业级的而非医用级，受试对象为个人，采集于受试对象接受0-9这10个数字的图像的刺激并进行相应的思考的时候。该数据库分为四个部分，如下图。

除了Insight数据之外，其他三个数据均提供一个受试对象未接受图像刺激的数据，如下图。

文件使用简单的txt文本文件，内部分为6列，分别为：

• id，简单的排序的序列号。
• 一个 2 字符的字符串，用于标识用于捕获信号的设备，“MW”代表 MindWave，“EP”代表 Emotive Epoc，“MU”代表 Interaxon Muse，“IN”代表 Emotiv Insight。
• 通道名称
• 一个 整数，用于标识被认为/看到的数字，可能值为 0、1、2、3、4、5、6、7、8、9 或者用于与任何无关的随机捕获信号数字-1。
• 一个 整数，用于标识在该信号的 2 秒内捕获的值的数量大小，由于每个设备的 Hz 不同，在“理论上”该值接近 MW 的 512Hz，EP 的 128Hz，220Hz对于 MU & 128Hz 对于 IN，每 2 秒。
• 一组以逗号分隔的数字，具有信号的时间序列幅度，每个设备使用不同的精度来识别从大脑捕获的电势： MW 和 MU 中的整数或 实数EP＆IN的情况。

文件中没有标题，每一行都是一个信号，字段之间用制表符分隔。

下面是使用VScode打开的MW.txt文件截图。

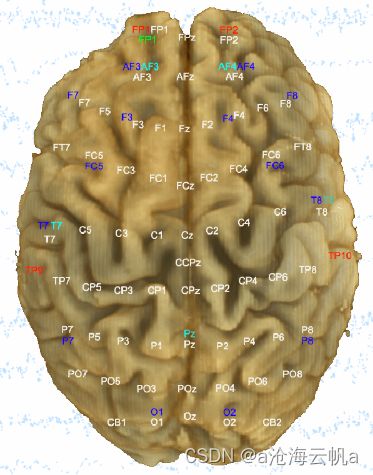
捕获信号的位置即信号通道如下。

信号描述

这里我仅使用MW中的数据进行展示，有兴趣的可以尝试一下其他数据。过程中，我使用支持向量机将信号进行一个二分类，其中一类为接受数字图像的刺激，另一类是不接受数字图像刺激，其中难免有数据不平衡的因素影响，但我认为可以忽略。并且从0-9的信号中提取可以将之分类的信息我已经尝试很久都无结果。
下面展示原始数据：
红色是接受刺激的信号，绿色则反之。
原始数据时域图

原始数据频域图

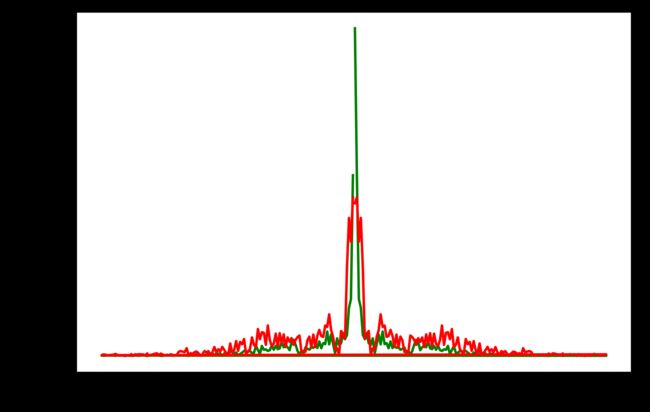
下面是使用小波硬阈值去噪后的数据展示：
去噪后时域图

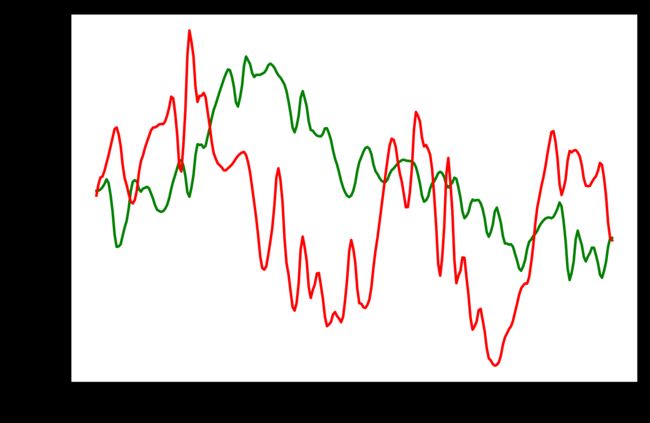
去噪后频域图

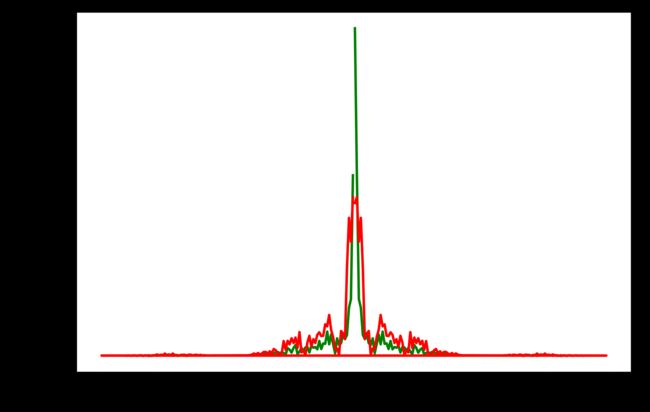
本文中直接将频域信号的归一化信号喂入支持向量机训练，下图是归一化的频域信号。

代码部分

下面将讲解相关代码。
首先导入所需要的库包括小波分解库pywt和数据处理库scipy：

import numpy as np
import pywt
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
from scipy import fft

下面是小波去噪函数，和文件存储位置，此处使用db4小波进行5尺度分解，一处cD1分量：

file_name = 'E:/database/MW.txt'#数据集文件

# 小波去噪预处理
def denoise(data):
    # 小波变换
    coeffs = pywt.wavedec(data=data, wavelet='db4', level=5)
    cA5,cD5, cD4, cD3, cD2, cD1 = coeffs

    # 阈值去噪
    cD1.fill(0)

    # 小波反变换,获取去噪后的信号
    rdata = pywt.waverec(coeffs=coeffs, wavelet='db4')
    return rdata

下面是从文件中读取相关数据，赋予数据新的标签，转换成ndarray对象，由于是使用频域特征，直接使用256点傅里叶变换即可，若是使用时域，则需要进行相应的填充：

labels = []
datas = []
with open(file_name, 'r') as f:
    file_data = f.readlines()
    for row in file_data:
        tmp_list = row.split('\t')                  #将原始数据每行使用制表符切分
        if tmp_list[-3] == '-1':                    #重新赋予标签
            labels.append(int('1'))
        else:
            labels.append(int('0'))
        tmp_list[-1] = tmp_list[-1].replace('\n','')#删除脑电数据最后一位的换行符
        predata = np.array([float(i) for i in tmp_list[-1].split(',')]).T                  #保存脑电数据
        denoise_data = denoise(predata)#去噪
        dataf = fft.fft(denoise_data,n=256)
        datas.append(np.abs(dataf))

labels = np.array(labels)
datas = np.array(datas,dtype=np.float32)

print(labels.shape,labels.dtype)
print(datas.shape,datas.dtype)

//下面是使用使用时域信号会用到的填充函数，这里我们不需要，给感兴趣的同学一个参考：

samples = 256

#填充
def padding(data, length):
    if length == samples:
        return data
    elif samples > length:
            return np.pad(data, (0, samples-length), 'mean')#使用平均值填充
    else:
        return data[:samples]

下面是可视化展示的代码：

x = fft.fftfreq(256,128)#计算频率中心，函数参数一是采样点数、参数二是采样频率
#绘制出频谱图，绿色是看数字的图片，红色是相反
plt.plot(x, datas[0],color='green')
plt.plot(x, datas[-1], color='red')

plt.show()

下面对数据进行归一化：

#归一化
scaler = MinMaxScaler()
new_data = scaler.fit_transform(datas)

可视化展示＋1：

#展示归一化后的频谱
plt.plot(x, new_data[0],color='green')
plt.plot(x, new_data[-1], color='red')
plt.show()

至此，数据预处理已经完成。下面使用机器学习模型进行训练：
首先打乱数据：

from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(new_data,labels)

然后喂入支持向量机：

from sklearn import svm
predictor = svm.SVC(gamma='scale', C=1.0, decision_function_shape='ovr', kernel='rbf')

predictor.fit(x_train, y_train)

预测结果：

from sklearn.metrics import accuracy_score
y_pre = predictor.predict(x_test)
accuracy_score(y_test, y_pre)

结果如图：

绘制混淆矩阵展示：

from sklearn.metrics import confusion_matrix
import seaborn
# 混淆矩阵
def plotHeatMap(Y_test, Y_pred):
    con_mat = confusion_matrix(Y_test, Y_pred)
    # 归一化
    # con_mat_norm = con_mat.astype('float') / con_mat.sum(axis=1)[:, np.newaxis]
    # con_mat_norm = np.around(con_mat_norm, decimals=2)
    ClassSet = ['Y','N']
    # 绘图
    plt.figure(figsize=(8,8))
    seaborn.heatmap(con_mat, annot=True, fmt='.20g', cmap='Reds')
    plt.xlim(0,2)
    plt.ylim(0,2)
    plt.xticks([0.5,1.5],ClassSet)
    plt.yticks([0.5,1.5],ClassSet)
    plt.xlabel('Predicted labels')
    plt.ylabel('True labels')
    plt.show()
plotHeatMap(y_test, y_pre)

下面是结果：

从结果来看，接受到数字图像的刺激产生的信号跟没有接受到刺激产生的信号是有显著性差别的。
就是搞不懂为啥我尝试了很多模型和去噪方法还是做不到将0-9的这些数据分开，在之前的实验中，分类准确率不超过15%，瞎蒙一个都比它准，希望有看到的大佬能够指点一二。

数据集介绍的图片源于MindBigData官网，本文不产生任何面向作者的利益。