数据库系统概述——第六章 关系数据理论(知识点复习+练习题)
博主:命运之光
专栏:离散数学考前复习(知识点+题)
专栏:概率论期末速成(一套卷)
专栏:数字电路考前复习
专栏:数据库系统概述
☀️博主的其他文章:点击进入博主的主页
前言: 身为大学生考前复习一定十分痛苦,你有没有过以下这些经历:
1.啊明天要考试了,关键这知识点它不进脑子啊。
2.小朋友,你是否有很多问号,为什么,快考试了你还啥也不会。
3.你们复习的时候,也是学着学着,手机就自动跳到手里了吗?
4.真正的大学生敢于直面崭新的课本。
5.睡也不敢睡,学也不想学。
6.监考老师+地理位置+附近战友友善度=考试分数。
当然以上都是开些玩笑,看看下面这些题,它可以让零基础未开始学习的你以最快的速度突击期末考试,知识点+练习题,突击起来效率嘎嘎快。
目录
☀️第六章 关系数据理论(重点)
1、设计性能较优的关系模式称为规范化,规范化主要的理论依据是(A)。
2、规范化过程主要为克服数据库逻辑结构中的插入异常,删除异常以及(C)的缺陷。
3、当关系模式R(A,B)已属于3NF,下列说法中(B)是正确的。
4、在关系DB中,任何二元关系模式的最高范式必定是(D)。
5、在关系模式R中,若其函数依赖集中所有候选关键字都是决定因素,则R最高范式是(C)。
6、根据关系数据库规范化理论,关系数据库中的关系要满足第一范式。下面“部门”关系中,因哪个属性而使它不满足第一范式?(B)。
函数依赖的概念
●平凡的函数依赖
●非平凡的函数依赖
例:在关系SC(Sno, Cno, Grade)中
例:学校教务的数据库:学生的学号(Sno)、所在系(Sdept)系主任姓名(Mname)、课程号(Cno) 成绩(Grade)
例:在关系Std(Sno, Sdept, Mname)中,有:
第一范式~BCNF
例:上例中,在S-L中存在非主属性对码的传递函数依赖,所以不属于3NF
例题:设有如下关系R
☀️练习题
☀️结语
☀️第六章 关系数据理论(重点)
本章内容:规范化、数据依赖的公里系统、模式分解
本章主要考点:函数依赖、多值依赖的概念、■范式判定、Armstrong公理系统
1、设计性能较优的关系模式称为规范化,规范化主要的理论依据是(A)。
A.关系规范化理论
B.关系运算理论
C.关系代数理论
D.数理逻辑
2、规范化过程主要为克服数据库逻辑结构中的插入异常,删除异常以及(C)的缺陷。
A.数据的不一致性
B.结构不合理
C.冗余度大
D.数据丢失
3、当关系模式R(A,B)已属于3NF,下列说法中(B)是正确的。
A.它一定消除了插入和删除异常
B.仍存在一定的插入和删除异常
C.一定属于BCNF D.A和B都是
4、在关系DB中,任何二元关系模式的最高范式必定是(D)。
A.1NF
B.2NF
C.3NF
D.BCNF
5、在关系模式R中,若其函数依赖集中所有候选关键字都是决定因素,则R最高范式是(C)。
A.2NF
B.3NF
C.4NF
D.BCNF
6、根据关系数据库规范化理论,关系数据库中的关系要满足第一范式。下面“部门”关系中,因哪个属性而使它不满足第一范式?(B)。
部门(部门号,部门名,部门成员,部门总经理)
A.部门总经理
B.部门成员
C.部门名
D.部门号
函数依赖的概念
函数依赖的定义:设R(U)是一个属性集U上的关系模式,X和Y是U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等, 而在Y上的属性值不等, 则称 “X函数确定Y” 或 “Y函数依赖于X”,记作X→Y。即只要 X 上的属性值相等,Y 上的值一定相等。
●平凡的函数依赖
在关系模式R(U)中,对于U的子集X和Y,
如果X→Y,但Y ⊆ X,则称X→Y是平凡的函数依赖
●非平凡的函数依赖
在关系模式R(U)中,对于U的子集X和Y,
若X→Y,但Y ⊈ X,则称X→Y是平凡的函数依赖
例:在关系SC(Sno, Cno, Grade)中
非平凡函数依赖: (Sno, Cno) → Grade
平凡函数依赖: (Sno, Cno) → Sno
(Sno, Cno) → Cno
部分函数依赖:若X→Y,但Y不完全依赖于X,则称Y对X部分函数依赖。记作
完全函数依赖:在R(U)中,如果X→Y,并且对于X的任何一个真子集X’,都有
, 则称Y对X完全函数依赖。记作
例:学校教务的数据库:学生的学号(Sno)、所在系(Sdept)系主任姓名(Mname)、课程号(Cno) 成绩(Grade)
U ={Sno, Sdept, Mname, Cno, Grade }
(Sno,Cno) →Grade是完全函数依赖,
(Sno,Cno)→Sdept是部分函数依赖
因为Sno →Sdept成立,且Sno是(Sno,Sanme)的真子集
●传递函数依赖:在R(U)中,如果X→Y,(Y X) ,YX, Y→Z,Z不属于Y, 则称Z对X传递函数依赖。
例:在关系Std(Sno, Sdept, Mname)中,有:
Sno → Sdept,Sdept → Mname
Mname传递函数依赖于Sno
第一范式~BCNF
第一范式(1NF):若关系模式R的每一个分量是不可再分的数据项,则关系模式R属于第一范式。
第二范式(2NF):若关系模式R∈1NF,且每一个非主属性完全函数依赖于码,则关系模式 R∈2NF 。(即 1NF 消除了非主属性对码的部分函数依赖则成为2NF)。
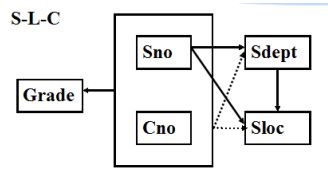
例:关系模式S-L-C(Sno, Sdept, Sloc, Cno, Grade)
Sloc为学生住处,假设每个系的学生住在同一个地方
函数依赖包括
(Sno, Cno) Grade
Sno → Sdept
(Sno, Cno) Sdept
Sno → Sloc
(Sno, Cno) Sloc
Sdept → Sloc
(虚线表示部分函数依赖)
由于非主属性Sdept和Sloc并不完全函数依赖于码(Sno, Cno),所以不是2NF解决方法:
S-L-C分解为两个关系模式,以消除这些部分函数依赖,这就属于2NF了
SC(Sno, Cno, Grade)
S-L(Sno, Sdept, Sloc)
第三范式(3NF):关系模式 R
成立,则称(每一个非主属性既不部分依赖于码有人不传递依赖于码)
例:上例中,在S-L中存在非主属性对码的传递函数依赖,所以不属于3NF
解决方法:采用投影分解法,把S-L分解为两个关系模式,以消除传递函数依赖:
S-D(Sno, Sdept)码为Sno
D-L(Sdept,Sloc) 码为Sdept
BCNF:关系模式 R
R
BCNF性质:若R∈BCNF
①所有非主属性对每一个码都是完全函数依赖
②所有的主属性对每一个不包含它的码,也是完全函数依赖
③没有任何属性完全函数依赖于非码的任何一组属性
例:在关系模式STJ(S,T,J)中,S表示学生,T表示教师,J表示课程。每一教师只教一门课。每门课由若干教师教,某一学生选定某门课,就确定了一个固定的教师。某个学生选修某个教师的课就确定了所选课的名称函数依赖:(S,J)→T,(S,T)→J,T→J (S,J)和(S,T)都是候选码
STJ∈3NF (S,J)和(S,T)都可以作为候选码,S、T、J都是主属性,没有任何非主属性对码传递依赖或部分依赖。但STJ不是BCNF,因为T是决定因素,T不包含码
解决方法:将STJ分解为二个关系模式: ST(S,T) ∈ BCNF, TJ(T,J)∈ BCNF
例题:设有如下关系R
| 课程名 |
教师名 |
教师地址 |
| C1 |
刘爽英 |
D1 |
| C2 |
乔志伟 |
D2 |
| C3 |
于得水 |
D2 |
| C4 |
井超 |
D2 |
(1)它为第几范式? 为什么?
(2)是否存在删除操作异常?若存在,则说明是在什么情况下发生的?
(3)将它分解为高一级范式,分解后的关系是如何解决分解前可能存在的删除操作异常问题?
解: (1)它是2NF。 因为R的候选关键字为“课程名”。依赖关系: 课程名→教师名,教师名 → 课程名,教师名→教师地址,所以课程名→教师地址。即存在非主属性“教师地址”对候选关键字课程名的传递函数,因此R不是3NF。但:因为不存在非主属性对候选关键字的部分函数依赖,所以R是2NF。
(2)存在。当删除某门课程时,会删除不该删除的教师的有关信息。
(3)分解为高一级范式如图所示。
R1(课程名,教师名)
| 课程号 |
教师名 |
| C1 |
刘爽英 |
| C2 |
乔志伟 |
| C3 |
于得水 |
| C4 |
井超 |
R2(教师名,教师地址)
| 教师名 |
教师地址 |
| 刘爽英 |
D1 |
| 乔志伟 |
D2 |
| 于得水 |
D2 |
| 井超 |
D2 |
分解后,若删除课程数据时,仅对关系R1操作,教师地址信息在关系R2中仍然保留,不会丢失教师方面的信息。
☀️练习题
☀️结语
❤️❤️一路看到这里,相信你的数据库考试应该已经增加了几分胜算
❤️❤️如果喜欢本文请不吝点赞,如果爱上本文请留下评论~
❤️❤️如果既不想点赞又不想评论…那么/(ㄒoㄒ)/~~还是祝愿你考试顺利啦~
![]()
#include
using namespace std;
int main()
{
cout<<"对编程,算法,人工智能,机器学习,深度学习,";
cout<<"图像处理,大数据挖掘,web前端网页设计等等感兴趣的同学";
cout<<"可以关注命运之光,命运之光正在努力学习,";
cout<<"不断的提升自己的专业能力,耗油跟,加加布鲁根!"< 再接再厉,继续加油!