leetcode - 2090. K Radius Subarray Averages

Description

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

Example 1:

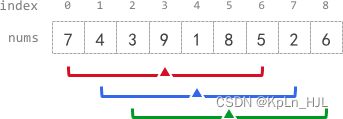
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

Constraints:

n == nums.length
1 <= n <= 10^5
0 <= nums[i], k <= 10^5

Solution

The most straightforward and brute way is to iterate the whole list, and for every element we calculate the k interval before and after, then calculate the average. Thus the time complexity will be $o(n\ast k)=10^{10}$, and this is unacceptable.

So we could use pre_sum to keep track of the sum, when we iterate the new element, simply minus the element at the previous boundary and add the element at the new boundary, this way the time complexity would be $o(n)$

Time complexity: $o(n)$
Space complexity: $o(1)$

Code

class Solution:
    def getAverages(self, nums: List[int], k: int) -> List[int]:
        res = []
        pre_sum = sum(nums[:2 * k])
        for i in range(len(nums)):
            if i - k < 0 or i + k >= len(nums):
                res.append(-1)
            else:
                pre_sum = pre_sum - (nums[i - k - 1] if i - k - 1 >= 0 else 0) + nums[i + k]
                res.append(pre_sum // (2 * k + 1))
        return res