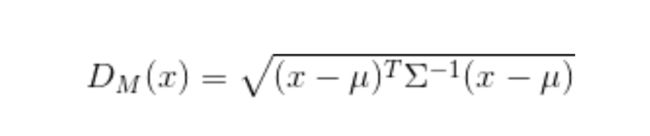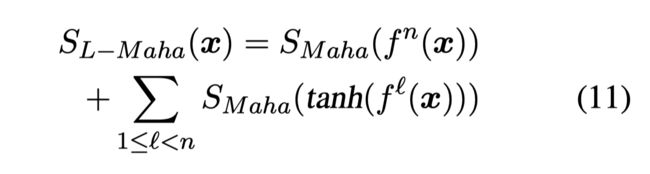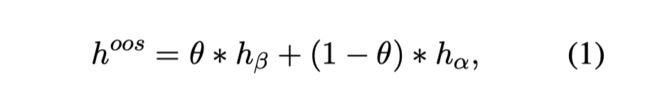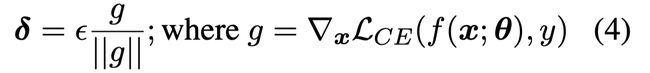论文笔记 - 对话系统中的 OOD （Out of Domain出域）问题

徐阿衡

人工智能与机器学习工程师

最近看了下 2021年关于 OOD 的几篇 paper，记录一下~

对话系统中的 domain 都是预先定义好的，而在实际应用场景中，会有很多现有系统回答不了的问题（out of the design scope），我们把系统支持的意图称为 in-domain (IND)，系统不支持的意图称为 out-of-domain (OOD)，OOD 是需要被拒识的。

处理 OOD 问题一般分为有监督和无监督两类方法。有监督方法相对更直接，收集好 OOD 数据，在 IND 和 OOD 上训练一个二分类器，或者直接学习一个 K+1 的分类器。然而 OOD 数据直接获取比较困难，所以有些研究是讨论怎么生成 pseudo outlier。另外，从直觉上看，IND 和 OOD 数据分布是不一致的，IND/OOD 数据极不平衡，在选择 OOD 数据时存在一定的 selection bias，很难选择到高质量有代表性的数据，所以学习的模型对没见过的 OOD 数据很难泛化。

而无监督方法往往在训练阶段只利用 IND 数据来学习 IND 的 decision boundaries（如 LMCL，SEG），在测试阶段使用额外的检测算法来检测 OOD。这类方法致力于更好的对 IND 数据建模，以及探索更好的检测方法。但由于训练和测试阶段的目标并不一致，容易对 OOD 数据产生 overconfident 的后验分数。下面是三类常见的检测方法：

• Probability Threshold: 利用 IND 模型的输出概率分布来决定 OOD，如 Maximum Softmax Probability (MSP)，或者对输出的分数进行若干操作转化如 ODIN, Entropy，也有一些是在 reconstruction loss 或者 likelihood ratios 上设定阈值
• Outlier Distance： 异常检测的方法，看 outlier 到 in-scope 集合的距离是否足够远。通常是在 embedding function 或者距离函数上做文章，如 Local Outlier Factor (LOF)、马氏距离等
• Bayesian Ensembles： 在 16-18 年的工作比较多，近两年没怎么看到，通过 IND 模型输出的方差来决定是否是 OOD，如通过 ensemble / dropout 等方式看模型输出的方差如果够大，就认为是 OOD。

总的来说，各类方法各有优缺点，并没有突破性的进展，依旧是道阻且长。

ACL 2021: Enhancing the generalization for Intent Classification and Out-of-Domain Detection in SLU

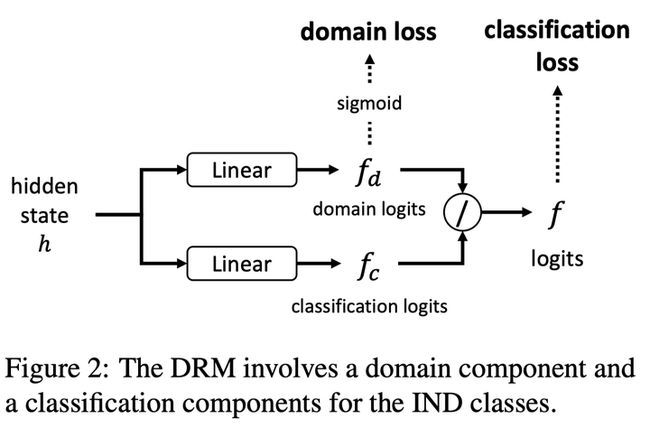
无监督方法。不需要额外收集数据，通过在最后一层线性层加上 DRM 模块就能实现。

模型

依据：

编码器对 query 进行编码得到 hidden state h，两个线性层得到(1)中的分母 domain_logits  和分子 classification logits ，相除得到新的 logits ，用  计算 IND 分类的损失，用  计算另一个损失 L_domain，作用是使得  接近 1（训练集里只有 IND），sigmoid 之前先对 进行裁剪，避免 的值过大，影响训练。两个损失相加得到最终损失。 

参数可以从 2.2-4 之间调，sigmoid(2.2) => 0.9，sigmoid(4) => 0.982

预测

OOD 的预测有 confidence-based 和 feature-based 两类方法

Confidence-based Methods

基于 softmax output 来输出 OOD 的预测分数

Feature-based Methods

这里提到了马氏距离，马氏距离修正了欧式距离中各个维度尺度不一致且相关的问题。马氏距离计算点与聚类（分布）之间的距离，在多维数据集异常检测，高维数据集分类应用中表现出色。

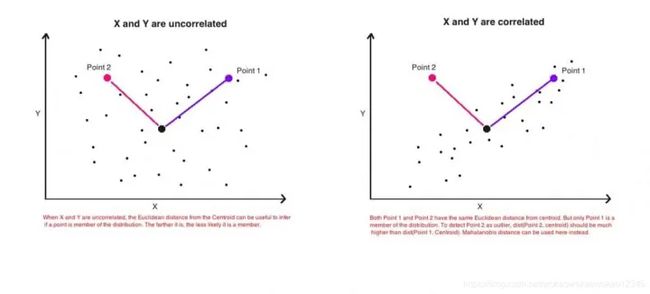
可以用下面两张图来理解欧式距离与马氏距离，如果 X, Y 两个维度不相关，欧氏距离可以很好的判别Point1和Point2距离聚类中心黑点的远近，而如果各维度不满足独立同分布的条件时，如右图，欧氏距离就无法很好的表征Point1和Point2谁是异常点了。因为两个点与中心的欧氏距离相等。但实际上只有蓝色点更接近该聚类。下图来自这篇博客：https://blog.csdn.net/wokaowokaowokao12345/article/details/115765116

简而言之，马氏距离将变量按主成分进行旋转，让维度间相互独立，然后进行标准化，让维度同分布。最后基本公式如下，x - μ 是样本到样本均值间的距离，Σ 是多维随机变量的协方差矩阵，如果协方差矩阵是单位向量，也就是各维度独立同分布，马氏距离就变成了欧氏距离。

对应到这篇 paper，

仅用最后一层 就有不错的效果了，具体的看 paper 吧。

作者额外提出了 L- Mahalanobis:

对 BERT 最后输出的每一层结果进行计算，�� 是第 l 层，�� 是最后一层。

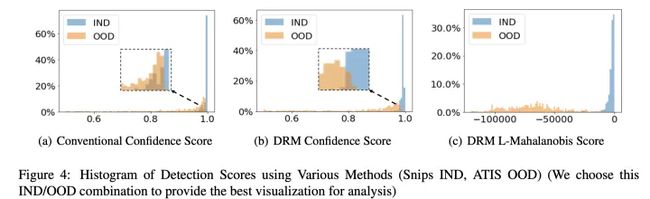
不同 detection score 的效果：

ACL 2021: Out-of-Scope Intent Detection with Self-Supervision and Discriminative Training

这一篇通过构建一系列的 pseudo outliers，然后把 intent classification 和 OOD 两个任务抽象为一个 K+1 的分类任务来做

Outliers 分为两种：

• hard outliers：和 inlier 很近，难以区分。可以通过不同各类别 inlier 的 feature 的 convex combination 来自监督的生成。如下， 和  是从不同类别采样的两个输入的表征，从均匀分布 U(0,1) 中采样。在 ablation study 里显示这部分带来的收益更大。

• easy outliers：和 inlier 较远，与 kown intent 很不相关，可以从 open_domain 数据集中抽取

训练和正常的预训练模型做分类任务一样。

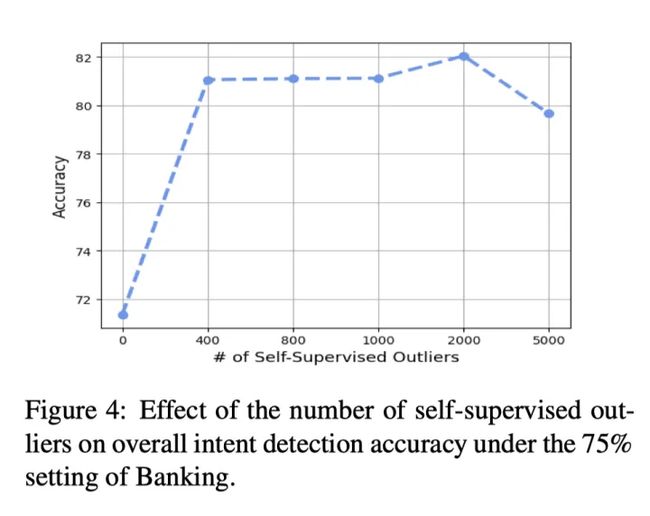
要注意的是 outlier 的数量对最终效果有较大影响。实验里的数据比例 # of inliers : # of open-domain outliers: # of self-supervised outliers = 1: 1: 4。

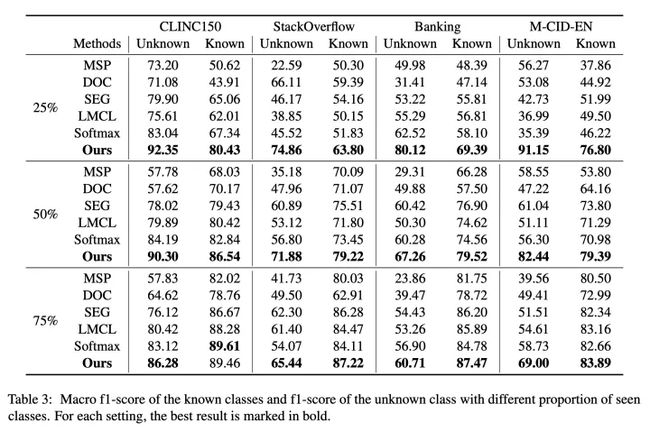
这篇的实验设置是用 k% 个 intents 作为 known intents 来训练，剩下的作为 unknown intents 作为测试集。

EMNLP 2021: GOLD: Improving Out-of-Scope Detection in Dialogues using Data Augmentation

弱监督方式，在少量有标签的 OOD 数据（seed data）以及一个辅助的外部数据集 (source data)上进行数据增强，产生 pseudo-OOD data。任务是 in-domain/out-of-domain 二分类。

两种增强的方法：

1. 在 OOD seed data 和 source data 的 embedding 空间里，对每个 seed 数据，通过 cosine 距离，从 source data 中找到 d 条与 seed 相似的数据，文中讨论 d= 24 对各个 source data 都是最优解
2. 对话增强方法：seed data 是多轮对话数据，通过把 dialogue 里任意一条 utterance 替换为 source data 的 matched utterance 来构建新的 dialogue

上面构建的增强数据有较大的噪声，一些数据与 IND 数据可能有 overlap，所以有个过滤机制来保证 candidates 是最有可能的 OOD。通过 baseline detector 的 ensemble 方法来进行投票选出最优的 OOD。

这篇的两个前提条件是很重要的，一是要有合适的 seed data，如果 seed data 数量减低一半效果会大打折扣（论文里限制 OOD 数量为 IND 样本的 1%），还有一个source data 的选取，需要和 target data 不同，但又不能完全不相关。构建的最理想的 pseudo-label 当然是在 IND 和 OOD 的 decision boundary 上了。

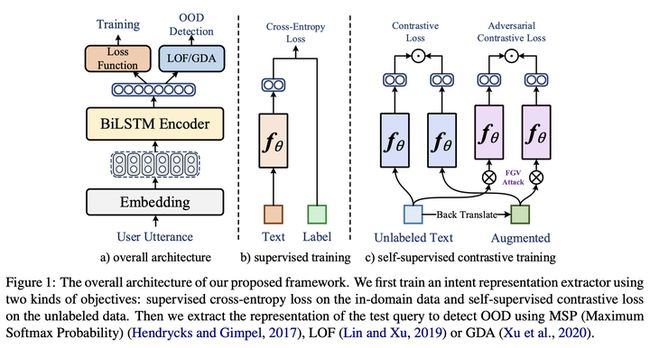
ACL 2021: Modeling Discriminative Representations for Out-of-Domain Detection with Supervised Contrastive Learning

idea很简单，有监督对比学习（SCL） + 交叉熵（CE）的方法，使用对抗攻击的方法实现正样本的增强。希望同一个意图下的样本互相接近，不同意图下的样本互相远离。有监督对比学习的表示学习方法可以通过最大化类间距离和最小化类内方差来提升特征的区分度。

属于无监督的OOD检测方法，训练阶段用IND数据，测试阶段用 MSP/LOF/GDA 来检测 OOD。

对比学习损失：

对抗攻击的样本增强，用 FGV 方式计算扰动

NACCL 2021: Adversarial Self-Supervised Learning for Out-of-Domain Detection

这篇和上面一篇都是美团发的文，模型上一篇更简单，实验指标也是上一篇更好看。

用 IND 数据和 CL loss 训练一个分类器，对 unlabeled data 进行对比学习，用 back translate 做正样本数据增强，

Back-translation 方法得到正样本对 (��, ��)，对抗攻击得到 (�����, �����)，实验了四种对比学习的设置

• Standard- to-Standard (S2S)，正样本对是 (��, ��)
• Adversarial-to-Adversarial (A2A)，正样本对是 (�����, �����)
• Standard- to-Adversarial (S2A)，正样本对是 (��, �����) / (��, �����)
• Dual Stream (DS)，正样本对是 S2S 和 A2A 相结合

最后是 DS 效果最好，也就是上图的方法，对比损失如下：

本文使用  WPL/s 发布  @GitHub