第七章 原理篇:HOG特征提取
之前面试被问到了然后没有讲出来,所以今天复习一下!
气死我了!
参考教程:
What Is a Feature Descriptor in Image Processing?
https://medium.com/analytics-vidhya/a-gentle-introduction-into-the-histogram-of-oriented-gradients-fdee9ed8f2aa
文章目录
- Feature Descriptors
-
- Local Descriptors
- Global Descriptors
- HOG feature descriptor
-
- steps to calculate HOG features
-
- 预处理
- 计算梯度
- 获得梯度直方图
- 归一化
- 获得特征向量
- 代码实现
随着机器学习的发展更迭,优化算法很容易被更先进的算法取代。而Histogram of Oriented Gradient方向梯度直方图检测算法,简称HOG则经历了时间的考验,即使在今天也被频繁使用,因为它的效果真的很好。
Feature Descriptors
“The feature descriptor describes an interest point and encodes the description in the form of a multidimensional feature vector in the vector space.” 特征描述子对图像中的感兴趣区域进行描述,并对描述的结果以多维度特征向量的形式进行编码。
那么什么是感兴趣区域interest point呢?这个区域通常是两个或多个区域的边缘段的交集或者物体的边界的方法发生快速改变的区域。这些区域具有一定的稳定性,在缩放、旋转或者光照改变时它们都具有一不变性,不会受到这些变化的影响。
因此,我们能够准确地找到这些区域,对于我们的图像相关的任务都会带来巨大的帮助。
特征描述子是一种提取对整个图像或者其中的感兴趣区域的特征描述的方法。它是对图像的表达,它提取了图像中有用的信息,抛弃了一些没有用的信息。特征描述子就像是一种数字化的指纹,它对重要信息进行编码,使得我们能使用这个编码结果将不同的特征区分开来。特征描述子在数学上的表达方式就是一维或者多维的向量,被称为特征向量。
从应用层面考虑,特征描述子可以简单分为两类。一种是对局部特征的描述,一种是对全局特征的描述。我们在一些low-level的应用上使用全局特征,比如目标检测和分类。我们在high-level的应用上使用局部特征,比如目标识别。
Local Descriptors
局部特征表达了一个图像的纹理。一个局部描述子通常对image中的一部分进行描述。使用多个局部描述子来处理一张图像要比只使用一个单独的描述子效果更好。常见的局部描述子有SIFT,SURF,LBP等。
Global Descriptors
全局特征将整个图片当作一个整体来进行描述,比如contour representation, shape descriptors, texture features。常见的全局描述子有HOG,HOF和MBH等。
HOG feature descriptor
使用HOG描述子,我们会将一个图像转换成一个长度为n的特征向量。虽然这个你很难通过这个向量得到原始图像的样子,但是它能够被应用在图像相关的任务中,并取得非常不错的结果。
在使用时,它只是简单地使用了梯度直方图作为图像的特征,对图像的局部区域梯度方向的次数进行了统计。
steps to calculate HOG features
在最开始的地方进行一下概念的总结:
window: 进行hog计算的区域称为window,要求宽高比1:2,一般使用64*128。
cell: hog中的最小单元,基于cell进行长度为9的梯度直方图的计算。
block: 2*2个cell组成一个block,基于block进行normalization。
预处理
图像大小:
- 首先对图像进行预处理,使其拥有一个固定的宽高比,通常这个比例是1:2。在实际使用中,一般选择64*128大小的图像,所以你需要先将你的图像转为64x128的大小。
- 假如你有一张很大的图片,你需要从图片中crop出一张张你想用来特征提取的小图片,并把它们转为指定大小。
- 这里的64*128,我们称为window。
灰度or RGB:
- 灰度图像和RGB图像都可以用来计算直方图,因此不是必须将图像转成灰度图的格式。假如使用的是彩色图像,就用多通道中最大的梯度代表当前位置的梯度。
色彩校正:
为减少光照因素的影响,可以对图像进行gamma矫正,调节对比度。
f ( x ) = x γ f(x) = x^{\gamma} f(x)=xγ
计算梯度
计算梯度直方图。使用以下的kernal对图像进行卷积操作,可以得到他们的水平和垂直方向的梯度。
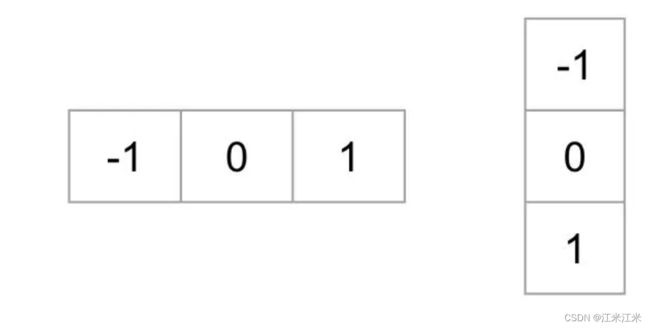
用公式的方法表示就是
G x ( r , c ) = I ( r , c + 1 ) − I ( r , c − 1 ) ; G y ( r , c ) = I ( r − 1 , c ) − I ( r + 1 , c ) G_x(r,c) = I(r, c+1) - I(r, c-1) ; G_y(r,c) = I(r-1, c) - I(r+1,c) Gx(r,c)=I(r,c+1)−I(r,c−1);Gy(r,c)=I(r−1,c)−I(r+1,c)
获得水平和垂直方向的梯度后,使用笛卡尔坐标都极坐标的映射公式来获得梯度的方向和幅值。
g = g x 2 + g y 2 g = \sqrt{g^2_x + g^2_y} g=gx2+gy2
θ = a r c t a n g y g x \theta = arctan\frac{g_y}{g_x} θ=arctangxgy
获得梯度直方图
在获得每个像素处的梯度后,梯度矩阵会被划分为8*8的小单元,称为cell。每一个cell中存在8*8*2=128个值。对每一个cell,都要计算一个长度为9的数组,也就是我们的直方图。bin值以20度为一个区间进行划分。如下图。

以下图为例子,对于cell中的第一个位置,方向角度为80,幅值为2,那么就在bin=80的位置加2。对第二个位置,方向角度36,幅值为3,那么这个3会按比例分配给bin=20和bin=40。对于角度大于160的值,图中画圈的位置,方向角度为165,幅值为85,那么它会被按比例分配给bin=0和bin=160.
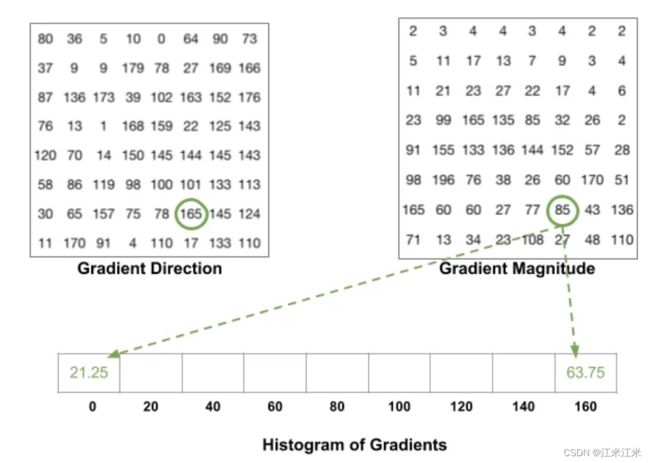
归一化
一个8*8的区域是一个cell,2*2个cell组成了一个block。这个block是使用滑动窗口得到的。一个cell中有9个值,那么一个block就有36个值。为了减少光照变化的影响,要对直方图进行归一化。使用L2范式,以block为单位进行归一化。
f b i = f b i ∣ ∣ f b i 2 ∣ ∣ + ϵ f_{bi} = \frac{f_{bi}}{\sqrt{||f_{bi}^2||+\epsilon}} fbi=∣∣fbi2∣∣+ϵfbi
获得特征向量
对一个block我们可以得到长度36的特征向量。假如图像大小是64*128,划分为8*16个cell,那么得到的block数目为(16-1)*(8-1) = 105。整个图像的特征向量长度为105*36 = 3780。
代码实现
import cv2
import math
import numpy as np
import matplotlib.pyplot as plt
img = cv2.resize(cv2.imread('car.png',0),(64,128))
img = np.power(img/float(np.max(img)), 1.5)
读取图像并进行gamma矫正。虽然hog可以提取彩色图像的特征,但是这里为了方便仍将图像转成了灰度图。
resize后真的很丑,将就看看。接下来进行图片梯度的计算,我们按照上一章节中提供的公式进行计算,而没有直接使用Sobel算子。
import math
def gradient_calculate(img):
gradient_x = []
gradient_y = []
mag = []
angle = []
h,w = img.shape
for i in range(h):
for j in range(w):
if j-1<0:
gx = img[i,j+1]
elif j+1 >= w:
gx = 0 - img[i,j-1]
else:
gx = img[i,j+1] - img[i,j-1]
if i-1<0:
gy = img[i+1,j]
elif i+1>=h:
gy = img[i-1,j]
else:
gy = img[i-1,j] - img[i+1,j]
gradient_x.append(gx)
gradient_y.append(gy)
mag.append(math.sqrt(gx**2 + gy**2))
if gx ==0:
angle.append(math.degrees(0))
else:
angle.append(math.degrees(abs(math.atan(gy/gx))))
gradient_x = np.array(gradient_x).reshape(h,w)
gradient_y = np.array(gradient_y).reshape(h,w)
mag = np.array(mag).reshape(h,w)
angle = np.array(angle).reshape(h,w)
return gradient_x, gradient_y, mag, angle
x, y, mag, ang = gradient_calculate(img)
输入为我们读取的图片,输出为gradient_x, gradient_y, mag 和angle。
看一下我们得到的结果。
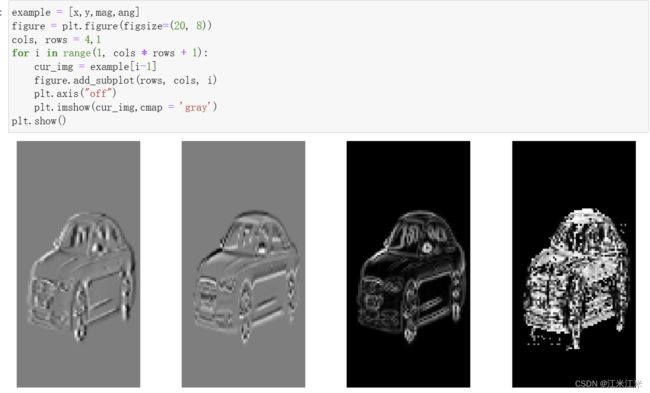
接下来对每个8*8的cell进行直方图的计算。我们使用上一步得到的mag和angle作为输入。
def histogram_calculate(mag, angle):
number_bins = 9
h, w = mag.shape
hist_out = []
for i in range(0,h,8):
tmp = []
for j in range(0,w,8):
patch_mag = mag[i:i+8,j:j+8]
patch_angle = angle[i:i+8,j:j+8]
bins = [0 for _ in range(number_bins)]
for m in range(8):
for n in range(8):
cur_mag = patch_mag[m,n]
cur_val = patch_angle[m,n]
index = cur_mag//20
if index == number_bins-1:
left = index * 20
right = 0
left = index*20
right = index*(20+1)
left_value = (cur_mag - left)//20 * cur_val
right_value = cur_val - left_value
bins[int(index)]+=left_value
bins[int((index+1)%number_bins)]+=right_value
tmp.append(bins)
hist_out.append(tmp)
return hist_out
hist = histogram_calculate(mag, angle)
这里返回结果的hist的大小为[16,8,9]。即对全图上所有的cell都进行了直方图的计算。接下来按照2*2的cell组成一个block,block按滑动窗口进行选取的规则,完成特征的计算,和block内部的normalization。
def calculate_feature(hist):
epsilon = 1e-05
feature = []
h, w = len(hist), len(hist[0])
for i in range(h-1):
tmp = []
for j in range(w-1):
block4 = [hist[m][n] for n in range(j,j+2) for m in range(i,i+2)]
block = []
for sample in block4:
for val in sample:
block.append(val)
summ = math.sqrt(sum([x**2 for x in block]))
block = [x/(summ+epsilon) for x in block]
tmp.append(block)
feature.append(tmp)
return feature
feature = calculate_feature(hist)
这里得到的feature大小为[15, 7, 36],也就是我们的图片的特征。
