深度学习中有监督，无监督， 自监督学习

1. 有监督

有监督学习的特点，是数据集通常带有人工标签的数据集。

1.1 定义

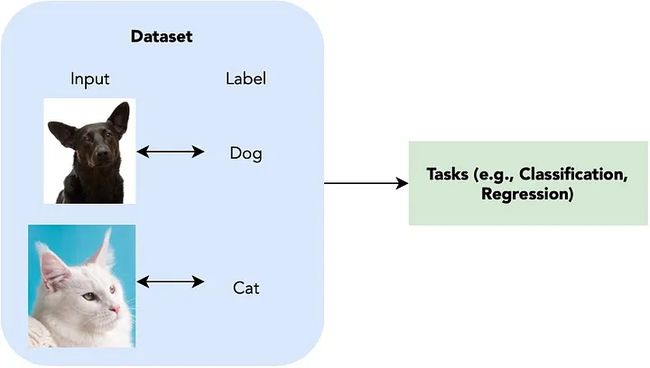
监督学习提供了一组输入输出对，这样我们就可以学习一个将输入映射到正确输出的中间系统。

监督学习的一个简单示例是根据图像数据集及其相应类别（我们将其称为标签）确定图像的类别（即，狗/猫等）。

对于给定的输入标签对，当前流行的方法是直接训练深度神经网络（即卷积神经网络）以从给定图像输出标签预测，计算预测与实际正确值之间的可微损失答案，并通过网络反向传播来更新权重以优化预测。

总的来说，监督学习是最直接的学习方法，因为它假设给定每个图像的标签，这简化了学习过程，因为网络更容易学习。

有监督学习的局限性，数据的标注过程是昂贵的。
虽然监督学习假设要训练任务的整个数据集对于每个输入都有相应的标签，但现实可能并不总是这样。

标记是一项劳动密集型处理任务，输入数据通常是不成对的。

1.2　半监督学习

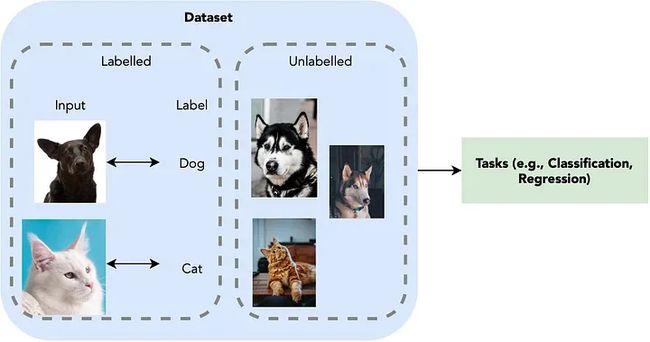
半监督学习旨在解决这个问题：我们如何使用一小组输入输出对和另一组仅输入来优化我们正在解决的任务的模型？

回顾图像分类任务，图像和图像标签现在仅部分存在于数据集中。是否可以在没有任何标签的情况下继续使用数据？

简短的回答是，是的。事实上，有一个称为伪标签的简单技巧可以做到这一点。首先，我们使用具有正确标签的图像来训练分类模型。然后我们使用这个分类模型来标记未标记的图像。然后将带有来自模型的高置信度标签的图像添加到模型中，并将其预测标签作为伪标签用于继续训练。我们迭代这个过程，直到所有数据都被用于最佳分类模型。

半监督学习的局限性：当然，这种方法虽然看似聪明，但很容易出错。如果标记数据的数量非常有限，则模型很可能对训练数据过度拟合，并在早期给出错误的伪标签，导致整个模型完全错误。因此，确定将输入伪标签对纳入训练的置信度阈值也非常重要。

为了避免模型在早期阶段过度拟合，还可以采用数据增强技术来增加训练规模并创建更广泛的数据分布。如果有兴趣，您还可以参考我关于混合作为图像分类任务最主要的增强策略之一的文章。

半监督和弱监督，都属于有监督的类型；
半监督或弱监督混淆：（半监督和弱监督）指的是在数据集中部分一些例子X没有标签，但是数据的人工标签是存在的。

1.3　弱监督学习

2. 自监督self-supervised learning

自监督，是指从输入数据中构建出标签或者监督信号；

它利用数据本身的固有结构或信息来创建训练的标签。自我监督学习不是依靠人类标记的数据，而是从输入数据中创建人工标签或监督信号。这些人工标签是使用特定的先验任务生成的，旨在捕捉数据中的有用信息或关系。

自监督学习是从数据本身找标签来进行有监督学习。
在自我监督学习(SSL) 中，您使用自己的输入X
（或修改，例如作物或应用数据增强）作为监督。

2.1关键思想

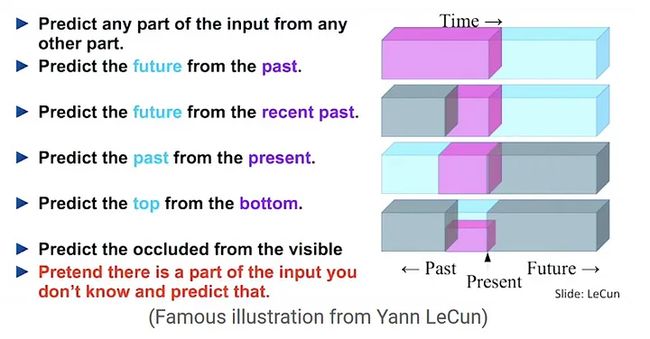
自监督学习的关键思想是设计一个先验任务，要求模型预测输入数据中缺失或损坏的部分。通过训练模型来解决这个任务，它学会了捕捉对下游任务有用的有意义的特征或表示。

自监督学习中的先验任务的例子包括预测图像的缺失部分（例如，绘画），预测shuffle 后的图像补丁的顺序，或预测视频中的未来帧。

SSL 主要用于预训练和表征学习。因此，在以后的下游任务中引导一些模型。

自监督学习的代表是语言模型，自监督不需要额外提供label，只需要从数据本身进行构造。

2.2 　对比学习（正负对）

正对:对相同的图像进行增强，并将它们标记为正对;

负对: 将不同的图像标记为负对，并尝试将负对的学习特征推开，同时将正特征拖近;

这使得网络能够学习对相似类别的图像进行分组，这进一步使得原本需要固定标签来学习的分类和分割等任务在没有给定基本事实的情况下变得可能。

2.3 自我预测方法

给定一个数据样本，我们尝试填充故意缺失的部分。例如，预测句子中的掩码词或为灰度图像着色。

2.4 自监督学习的模型

Barlow Twins 架构于 2021 年 6 月首次在论文“Barlow Twins: Self-Supervised Learning via Redundancy Reduction”中提出。Barlow twins 的名字来源于神经科学家 H. Barlow，他在 1961 年的工作启发了这种架构。它是一种最先进的 ssl 方法，它依赖于直观且易于实现的想法。

最近的自监督学习研究的目标是学习对输入样本失真不变的嵌入。这是通过对输入样本应用扩充并尽可能“驱动”它们的表示来实现的。但一个反复出现的问题是存在微不足道的常数解。当网络依赖于这种微不足道的解决方案时，就不会发生有意义的学习。

已经提出了许多自监督模型和架构（BYOL、SimCLR、DeepCluster、SIMSIAM、SELA、SwAV）。Barlow twins 在几个计算机视觉下游任务上的表现优于或与大多数方法相当。

与其他自监督方法类似，Barlow twins 旨在学习对输入失真不变的表示（嵌入）。它通过 3 个步骤实现。

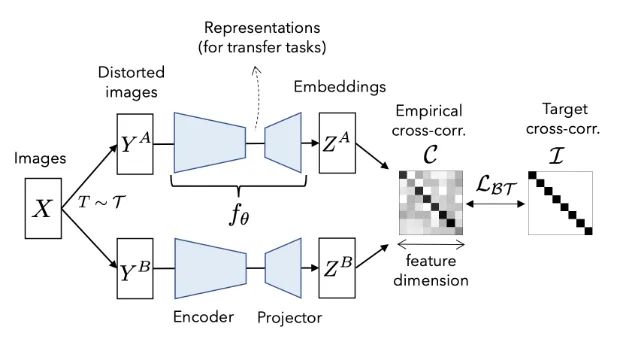
将两组不同的增强应用于同一输入样本 X，导致同一图像的两个扭曲视图 (Y^a, Y^b)。
扭曲的视图被送入完全相同的编码器，在下面的图 1 中表示为 f。我们将这两个输出分别称为 Z^a、Zb。
计算两个嵌入向量的互相关矩阵 M。应用损失，计算矩阵 M 与单位矩阵 I 的距离。

一个重要的细节是编码器 f 实际上是由一个编码器网络和一个“投影仪”网络组成的。我们将编码器的输出称为“表示”，将投影仪的输出称为嵌入。编码器执行特征提取，而投影仪设计嵌入的高维空间。学习到的表示用于在下游任务上训练分类器，而嵌入被馈送到损失函数中以训练模型。

由于失真表示不变是我们的主要目标，因此编码器 f 在同一样本的失真视图上生成的嵌入应该几乎相同。如果它们相同，则互相关矩阵 M 将等于单位矩阵。通过最小化我们的损失函数，我们尽可能接近它们的嵌入和表示。此外，通过将 M 驱动到单位矩阵 I，我们将彼此的嵌入维度去相关。

2.4　自监督学习的优势

• 无需人工标注
  高质量的标记数据很昂贵，而且通常很稀缺。自监督训练方法不依赖人工标签来学习有用的特征。这使我们能够利用野外可用的大量数据。

像 BERT 或 GPT-3 这样的大型语言模型之所以出奇地有效，不仅仅是因为它们的体积庞大。这些模型是在 huuuge 文本语料库上训练的。互联网是他们的游乐场，他们可以自由地从书籍、维基百科和常见互联网站点中的所有文本中学习。

另一方面，视觉模型可以收集 Instagram 照片和 youtube 视频进行训练。这使他们能够建立更多的常识

• 模型可扩展

上述观点的直接结果是，使用 SSL 方法训练的模型可以而且确实可以扩展到前所未有的规模。其他技术因素，如更好的硬件，也有助于此。但是由于较大的模型有更多的参数需要优化，因此在训练过程中需要更多的数据。SSL 是满足庞大模型数据需求的唯一途径。

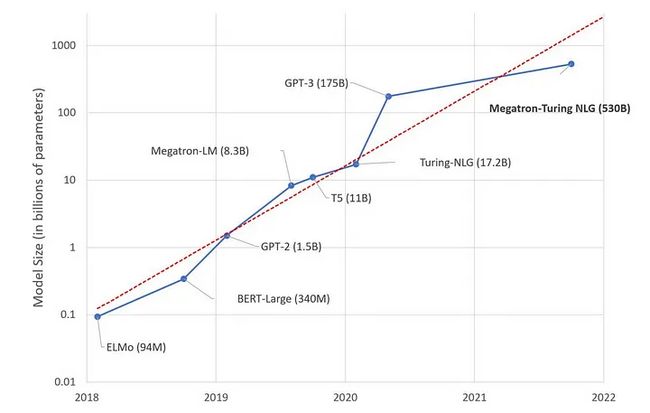
GPT-3 有 1750 亿个参数，甚至不再是最大的模型。如果我们依赖于带注释的数据，那么结果要么非常糟糕，要么训练成本非常高。然而，不断增加的大型模型可能并不是 AI 可遵循的最佳路径。

通过自我监督学习，模型可以扩大规模，从而使它们更有效并提供更多容量。将我们带到下一点的东西。

• Zero shot 零样本的迁移学习能力
  自监督模型似乎具有的一个巨大优势是它们能够处理未明确接受过训练的多项任务。他们有能力将他们的知识零样本转移到新的下游任务上。

CLIP 是一个经过训练的模型，可以为给定图像找到最合适的文本片段（在许多文本片段中）。尽管它从未在图像分类、目标检测或图像分割等其他任务上接受过明确的训练，但它能够在 30 种不同的任务中取得相当不错的性能。

如果他们在新任务上表现出色的先天能力也得到了一些标记样本（比如原始数据集的 1% 或 10%）的补充，那么自监督模型可以匹配甚至优于在完整数据集上训练的完全监督模型！

用 Yann LeCun（META AI 首席人工智能科学家）的话来说

我们认为，自我监督学习 (SSL) 是在 AI 系统中构建背景知识和近似常识形式的最有前途的方法之一。

2.4　自监督学习的缺点

与生活中的大多数事情一样，自我监督学习也有其自身的缺点和局限性。认识它们是改善它们的第一步。

• 计算能力
  由于数据集和模型都更大，自监督训练方法的计算成本通常比监督训练方法高。这对个人、小型组织，甚至一些大学来说都是一个瓶颈。

提高这些方法的训练效率是一个非常有价值的研究方向。开源模型权重也有助于小型组织使用这些模型。

• 先验任务设计
  设计先验任务具有挑战性，会影响模型的下游能力。根据最终应用程序，一些先验任务可能比其他任务更合适。这同样适用于某些方法工作所必需的数据扩充。与经典的监督学习范式相比，这又增加了一层复杂性。

3. 无监督 unsupervised

无监督学习只有输入数据没有相应的分类或标签。目标是找到每个数据集的潜在模式。

涉及无监督学习的任务包括客户细分、推荐系统等等。然而，一个模型如何在没有任何标签的情况下学习任何东西？

无监督学习不依赖任何标签值，通过对数据内在特征的挖掘，找到样本间的关系，比如聚类相关的任务；

无监督学习是机器学习的一种类型，算法在没有明确标签或预定输出的情况下学习数据中的模式、关系或结构。

其目的是发现数据中的固有模式或分组。

3.1 　无监督学习过程

算法在没有任何具体指导的情况下探索数据以寻找有意义的模式或表征。

它通常被用于类似数据点的聚类，识别异常值，或发现数据中的隐藏结构等任务。无监督学习也可以作为监督学习任务的预处理步骤，学到的表征可以帮助提高性能。

无监督学习没有标拟合标签的过程，而是从数据分布的角度来构造损失函数。
在无监督学习(UL) 中根本没有监督；

无监督的代表是聚类。

3.2　无监督常见算法

由于我们对每个输入标签都没有“正确答案”，因此以某种方式找到模式的最佳方法是对它们进行聚类。也就是说，给定一组数据特征，我们试图找到彼此相似的特征并将它们组合在一起。一些聚类方法包括 K-Means 和 K-Medoids 方法。

仅仅聚类实际上可能会产生大量的见解。以推荐系统为例：通过根据用户的活动对用户进行分组，可以将一个用户喜欢的内容推荐给另一个用户，而无需明确了解每个用户的兴趣是什么。

无监督学习中使用的常见算法包括聚类算法（如k-means聚类）、降维技术（如主成分分析）和生成模型（如高斯混合模型）。

密度估计、降维（例如 PCA、t-SNE）和聚类（K 均值），至少从经典的 ML 前景来看是完全不受监督的：例如 PCA 只是试图保持方差

UL，至少在经典 ML 中，用于密度估计和聚类。

3.3　无监督与自监督的关系

无监督学习是一个更广泛的类别，模型从无标签的数据中学习，而自我监督学习是无监督学习中的一个特定方法，从数据本身产生人工标签或监督信号。自监督学习由于能够在不需要大量标签数据的情况下学习有意义的表征而得到了普及

实际上，在现代无监督深度学习方法中，事情变得更加模糊，这些方法倾向于混合 SSL 和 UL 的方法，例如也具有密度估计头的 AE。甚至嵌入首先由 SSL 学习，然后以无监督的方式针对聚类进行微调。