第二章 数据结构(一)——链表,栈和队列与kmp
文章目录
-
- 链表
- 栈和队列
-
- 表达式运算
- 单调栈
- 单调队列
- kmp
- 链表练习题
-
- 826. 单链表
- 827. 双链表
- 栈和队列练习题
-
- 828. 模拟栈
- 3302. 表达式求值
- 829. 模拟队列
- 830. 单调栈
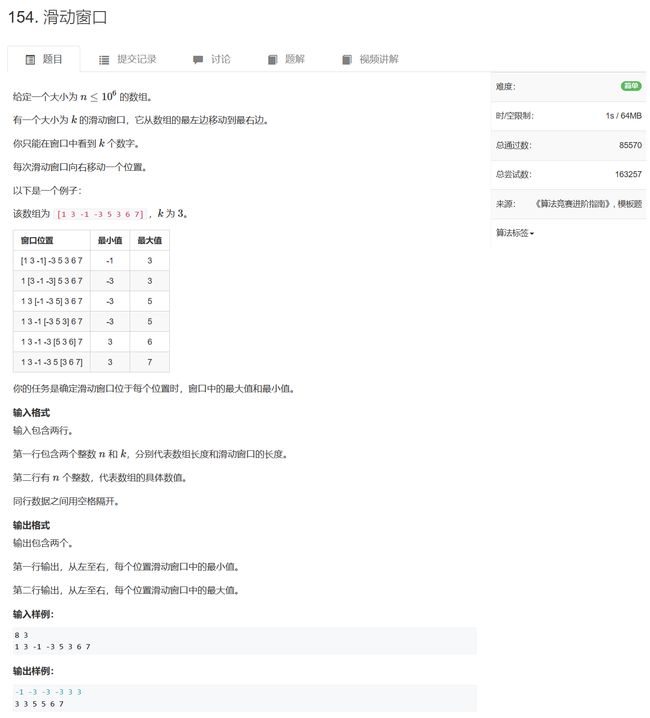
- 154. 滑动窗口
- kmp练习题
-
- 831. KMP字符串
kmp虐我一下午
链表
若用链式结构实现链表,效率低,因为new的开销大
采用数组的方式实现,可以提高某些算法的速度,不会卡时间
- 单链表:常被使用为邻接表,存储图和树
实现:
e[i]:数据域,存储val值
ne[i]:指针域,存储下标,指向空节点的ne[i]为-1
idx:存储当前使用节点的后一个未使用节点,注意:这样将导致内存泄漏,但算法中不用考虑内存泄漏问题
e和ne用下标关联,如以下板书

y总没有仔细区分头节点与头指针两个概念,一开始看注释看得有些懵,后来发现是y总没有特别强调这两个概念。其实y总的链表实现是不带头节点(也就是常说的哨兵位)的实现,也就是说只有头指针。但是代码的注释中却出现了头节点的字眼,以下链表的实现为带头节点版本,因为带上头节点的操作更为灵活
带头节点单链表的模拟:
// ne数组的0号下标作为head指针,e数组的0号下标不存储任何有效数据
// 所以0号位置是头节点的位置,头节点只是为了操作方便,不存储任何有效值
int e[N], ne[N];
int idx = 1;
// 在第k个插入的数之后插入节点
void insert(int k, int x)
{
e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++;
}
// 头插,在头节点之后插入
void push_front(int x)
{
insert(0, x);
}
// 删除第k个插入的数之后的节点
void erase(int k, int x)
{
ne[k] = ne[ne[k]];
}
// 链表的输出
void print()
{
for (int i = ne[0]; i; i = ne[i]) printf("%d ", e[i]);
}
注意:第k个插入的节点在数组中的下标为k
当erase的k为0时,表示删除头节点之后的数,也就是第一个插入的数。若链表为不带头节点的实现,那么这个操作就需要特判。带上头节点后,这个操作直接erase(0)即可
- 双链表:可用来优化某些问题
与单链表的指针域不用,双链表的指针域有两个指针。所以使用l[N]与r[N]表示其前后(左右)节点,
带头节点双链表的模拟:
int l[N], r[N], e[N];
int idx = 1;
// 初始化
void init()
{
l[0] = 0, r[0] = 0;
}
// 往第k个插入的节点右边插入节点
void insert(int k, int x)
{
e[idx] = x;
r[idx] = r[k], l[idx] = k, l[r[k]] = idx, r[k] = idx ++;
}
// 删除第k个插入的节点
void erase(int k)
{
r[l[k]] = r[k], l[r[k]] = l[k];
}
栈和队列
用原生数组模拟实现栈与队列,速度会比STL快一些
栈的模拟:
// 初始化,stk为存储栈元素的原生数组,tt为栈顶指针
// 注意:tt一开始指向0,但是栈元素从1下标开始使用
// 所以当tt指向0时,说明栈为空
int stk[N], tt;
// 入栈
stk[++ tt] = x;
// 出栈
-- tt;
// 判栈
return tt == 0;
// 返回栈顶元素
return stk[tt];
注意,以上代码没有合法性判断,只关注结构的实现
队列的模拟:
// 初始化,q为存储队列元素的原生数组
// tt为队尾指针,hh为队头指针
// tt一开始指向-1,hh一开始指向0,此时队列为空
// 也就是tt < hh时,队列为空,tt >= hh时,队列不为空
int q[N], hh, tt = -1;
// 入队
q[++ tt] = x;
// 出队
++ hh;
// 判空
return tt < hh;
// 返回队头元素
return q[hh];
表达式运算
表达式求值也是一个模板,具体看练习题
单调栈
运用场景:给定一个序列 a n a_n an,求这个序列中每一个数的左边,距离它最近,且比它小的数在什么地方?输出这个序列
首先思考暴力解法,遍历序列中的每个数 a k a_k ak,对于每次的遍历,从 a k − 1 a_{k-1} ak−1开始往左遍历。直到找到比 a k a_k ak小的数或者遍历完左边的所有数,输出该数(若遍历完所有数,输出-1)并遍历下一个数 a k + 1 a_{k+1} ak+1
在 a k a_k ak左边的数中,对于其中两个元素 a i a_i ai与 a j a_j aj,若满足i < j && a i a_i ai > a j a_j aj
因为 a i a_i ai > a j a_j aj,且 a i a_i ai比 a j a_j aj后遍历到,不论 a j a_j aj与 a k a_k ak是否满足小于关系,对于 a k a_k ak的遍历,因为 a j a_j aj的存在, a i a_i ai永远不可能是比 a k a_k ak小的数
若 a j a_j aj大于 a k a_k ak,那么大于 a j a_j aj的 a i a_i ai肯定是大于 a k a_k ak的
若 a j a_j aj小于 a k a_k ak,那么关于 a k a_k ak的遍历最终会在 a j a_j aj停下,不可能遍历到 a i a_i ai
假设我们用栈完成暴力解法中对 a k a_k ak的一次遍历,栈存储了 a k a_k ak左边所有的数,并且栈顶为 a k − 1 a_{k-1} ak−1
此时我们只要不断地将栈顶元素出栈,判断该元素是否小于 a k a_k ak,直到栈为空或者找到小于 a k a_k ak的数
根据刚才的推导,对于 a k a_k ak左边的所有元素,若满足i < j && a i a_i ai > a j a_j aj,在这样的逆序对中 a i a_i ai是没有必要存储的。因此在元素入栈时,若入栈元素与栈顶元素构成了逆序对,那么删除栈顶元素,直到两者不构成你逆序对或者栈为空,将元素入栈
根据以上入栈算法,我们能保证栈中的元素是单调的,单调上升
当我们要找距离 a k a_k ak最近且在 a k a_k ak左边的元素时,需要先用 a k a_k ak左边的元素构建单调栈,然后按照以上入栈算法将 a k a_k ak入栈
若经过入栈算法维护后的栈为空,说明 a k a_k ak左边没有数小于 a k a_k ak
若经过入栈算法维护后的栈不为空,此时的栈顶为距离 a k a_k ak最近且在 a k a_k ak左边的小于 a k a_k ak的元素
int a[N], stk[N];
for (int i = 0; i < n; ++ i)
{
// a[i]入栈前的维护
while (栈不为空 && 栈顶元素与a[i]构成逆序对) pop栈;
if (栈不为空) 输出栈顶元素;
else 输出-1;
将a[i]入栈;
}
单调队列
运用场景:求给定一个数组,求长度为k的滑动窗口中的最大值/最小值
比如输出窗口大小为3的最小值
与单调栈一样,先思考暴力解法,挖掘其单调性,后优化算法
若窗口大小为k,那么从第k个元素开始,往后遍历所有的元素
每次的遍历都要往前遍历k个元素,找出其中的最大值/最小值
这样暴力解决,时间复杂度为O(nk),n为数组长度,k为窗口长度
考虑如何优化:求滑动窗口中的最小值时
假设窗口中有k个元素,对于其中两个元素 a i a_i ai与 a j a_j aj,满足i < j && a i a_i ai > a j a_j aj
那么根据窗口的滑动, a i a_i ai会比 a j a_j aj先退出滑动窗口,可以理解为队列的先进先出,因为 a i a_i ai比 a j a_j aj先进入滑动窗口,那么 a i a_i ai就会比 a j a_j aj先退出滑动窗口
而 a i a_i ai > a j a_j aj,且 a i a_i ai比 a j a_j aj先退出窗口(i < j)。只要 a i a_i ai与 a j a_j aj同时存在,滑动窗口的最小值只可能是 a j a_j aj,不可能是 a i a_i ai,所以此时的 a i a_i ai是无效元素,没有必要在窗口中记录该元素
由此,我们可以推导更普遍的情况。即窗口中不允许i < j且 a i a_i ai > a j a_j aj这样的逆序对出现,即窗口中的元素是单调的,单调上升
当 a i a_i ai进入窗口时, a i a_i ai将比窗口中所有的元素迟出窗口(存在时间更久)。若队尾(窗口右侧)的元素大于 a i a_i ai, a i a_i ai 进入窗口后,将出现逆序对。所以此时需要删除队尾元素,重复上面的比较步骤,直到队尾与 a i a_i ai不构成逆序对,或者队列为空时,比较结束,将 a i a_i ai入队
根据以上的入队算法,我们能保证窗口中的序列是单调上升的,此时窗口中的最小值为窗口左侧(队头)元素
所以对于 a n a_n an这个序列,我们只要线性遍历一次,将每个元素按照以上的入队算法依次入队。每个元素入队后(某个滑动窗口)的最小值就是队头元素,其中涉及到一些边界的细节问题,将在练习题的代码中呈现
// 分别存储所有元素以及滑动窗口中的元素在a数组中下标
int a[N], q[N];
for (int i = 0; i < n; ++ i )
{
if (队列不为空 && 窗口的长度超过了k) hh ++; // 窗口向右滑动时,删除左侧元素
// 窗口向右滑动时,元素将要入队
// 采用双端队列的方式,维护窗口的单调性
while (队列不为空 && 队尾元素与将入队元素构成逆序对) -- tt;
// 窗口向右滑动时,维护完单调性,元素入队
q[++ tt] = i;
if (窗口长度为k) 输出最小值(队头元素);
}
kmp
- S串:文本串,P串:模式串
- 遍历S串,在S串中找P串
kmp的精髓是next数组,代码中用ne[N]表示该数组
kmp使用双指针实现,用i遍历S串,j遍历P串,其中i不会出现回退,当S[i] != P[j + 1]时, j会发生回退
需要注意的是,S串和P串的0号位置不存储任何值,两串都从1号下标开始存储有效值
并且i从1开始,j从0开始,每次都是比较S[i] == P[j + 1],为什么j不从1开始?这个看个人习惯,j从0开始的话,代码比较好写
现有S串:aaaaaaaaa,P串:aaaac。思考暴力做法,用i遍历S串,尝试以S[i]开头的子串与P串进行匹配,若匹配失败,i ++。尝试以S[i + 1]开头的子串与P串的匹配,可以发现在这个过程中,虽然i不会回退,但是产生了多次重复的比较
比如第一次比较时,S串的前4个字符和P串的前4个字符匹配,但第5个字符不匹配。下一次进行的比较将重复比较前4个字符中的后三个,这样的重复比较有很多。为消除这样的重复比较,可以使用kmp算法
首先需要理解ne数组,理解ne数组首先要理解前缀与后缀两个概念,一个字符串中,后缀的终点固定,前缀的起点固定。现有字符串:ababa,该字符串中后缀的终点为最后一个字符a,前缀的起点为第一个字符a。现有问题,是否存在长度相等并且内容也相等的前缀与后缀(前缀与后缀不包括字符串本身)?
- 若存在,请返回长度最长的前缀与后缀的长度(或者是长度最长的前缀的终点)
- 若不存在,返回前缀的起点
显然,ababa中,最长前缀的终点为第三个字符,也就是中间的那个a。以上问题应该返回该字符的下标
对于P串的每个子串,都要解决以上问题,问题的答案将构成ne数组
ne数组的含义:ne[j]保存了以P[j]为终点,和该后缀相等,并且以P[0]为起点的最长前缀的终点
ababa的例子中,ne[0] = 0, ne[1] = 0, ne[2] = 1, ne[3] = 2, ne[4] = 3
保存相同的最长前后缀有什么用?在P串尝试匹配S串时,遇到一个不匹配字符,就说明了在P串中,该字符之前的所有字符和S串的某一部分匹配。为减少重复的比较运算,找出这些字符的最长前后缀,因为这些字符和S串的某部分是相同的,那么这些字符串的后缀和S串的某部分的后缀也是相同的,和后缀相同的前缀与S串的某部分的后缀也是相同的。此时我们就能舍弃最少的尾部字符,从前缀的后一个字符开始比较
因此,当S[i] != P[j + 1]时,需要更新j = ne[j]。当前要匹配的是p + 1,说明P[0, j],和S串的某部分匹配,找到此时最长前缀的终点ne[j],再匹配S[i]与P[j + 1]。若两字符不匹配,j将一直更新。也就是说P串和S串匹配的字符越来越少,直到j为0,此时退无可退
所以,kmp的比较本质是字符的比较。用i从下标1开始遍历S串,j从下标0开始遍历P串,当S[i] != P[j + 1]时,需要更新j,找到一个最长前缀,用其之后的字符(同样是P[j + 1])再与S[i]比较
当更新结束,可能是两种情况
一是S[i] == P[j + 1],此时j ++,表示P串有字符和S串匹配。若这时的j走到P串结尾,说明找到S串的某个子串和P串匹配。因为kmp需要在S串中,找出所有和P串匹配的子串,因此此时还需要更新j = ne[j]。用相等的最长前缀再次开始匹配
二是S[i] != P[j + 1],说明在S串种,不论怎样更新j,都没有和P[j + 1]匹配的字符。此时什么都不做
在kmp比较前,需要预处理ne数组。ne数组的构建也是双指针,不过是两个指针遍历同一序列,而kmp的比较是两个指针遍历不同序列。i从P串的第二个字符开始(因为此时才有前缀和后缀),i = 2,j从第一个字符开始,j = 0。同样,每次比较P[i] == P[j + 1],若不相等,更新j。更新完成时
若P[i] == P[j + 1],j ++
否则说明不论怎样更新都没有P[j + 1] == P[i],此时j不变
最后,ne[i] = j,表示与以i为终点后缀相等的最长前缀的终点是j
以上,描述可能存在着差一错误,在实现代码时,需要注意边界问题
模板:
const int M = 1e6 + 10;
const int N = 1e5 + 10;
char p[N], s[M];
int m, n, ne[N];
for (int i = 2, j = 0; i <= n; ++ i )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) ++ j;
ne[i] = j;
}
for (int i = 1, j = 0; i <= m; ++ i )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) ++ j;
if (j == n)
{
printf("%d ", i - n);
j = ne[j];
}
}
链表练习题
826. 单链表
#include 827. 双链表
#include y总的实现中,将数组的0号与1号位置作为双链表的头尾节点,即带有两个哨兵位的双链表
初始化时:l[1] = 0, r[0] = l,可以发现l[0]以及r[1]没有使用,当然初始化时也可以l[0] = 1, r[1] = 0
这个看个人习惯,我习惯只使用一个头节点,初始化时:l[0] = 0, r[0] = 0
遍历双链表时,从头节点的下一个节点(第一个存储有效数据的节点)开始遍历,直到遇到头节点就结束(因为是循环双链表)
y总实现的双链表是不循环的,遍历时遇到尾节点(尾哨兵位)时停下
以及,在双链表的最右侧插入一个节点时,不能insert(idx - 1, x),应该insert(l[0], x)
idx - 1不是链表的最右侧,只有在第idx - 1次插入的节点没有被删除的情况下,该节点才是链表的最右侧
而l[0]表示头节点的左侧节点,因为链表的是循环的,所以该节点是链表最右侧的节点
在第k个插入的数左边插入一个节点时,不能insert(k - 1, x),同理,第k个数左边的节点应该是l[k],所以要写insert(l[k], x)
栈和队列练习题
828. 模拟栈
#include 3302. 表达式求值
与后缀表达式求值不同,中缀表达式求值需要使用两个栈模拟。一个数字栈,一个符号栈
遍历表达式,遇到数字直接入栈。遇到符号也要入栈,不过需要判断符号栈的栈顶符号优先级是否大于等于要入栈的符号
若栈顶符号优先级大于等于要入栈的符号,那么需要进行eval运算
eval运算:取出符号栈的栈顶元素一次以及取出数字栈的栈顶元素两次,根据取出的符号进行二元运算,将运算结果入数字栈
遍历表达式时,若符号栈的栈顶符号优先级大于等于要入栈的符号,进行eval运算,直到栈为空或者栈顶符号优先级小于等于要入栈的符号
因为栈的性质决定靠近栈顶的元素先出栈,在表达式计算中,靠近栈顶的符号先被运算
因此我们要使优先级越高的符号越靠近栈顶,从栈底到栈顶,符号的优先级顺序是从低到高升高的
当一个元素入栈后破坏了这种单调性,为了维护单调性,我们需要pop栈顶元素,使栈顶元素的优先级小于要入栈的符号,从而使该符号入栈后,栈仍然具有单调性
当表达式被遍历完,符号栈中还有元素,我们需要不断地进行eval运算,直到符号栈为空
此时数字栈中只有一个元素,该元素就是表达式运算的结果
需要注意的是,表达式中可能含有括号,对于括号我们需要特判。遇到左括号时将其入栈,左括号与右括号之间也具有单调性,注意:括号维护的单调性与原表达式维护的单调性可能不连续
因此维护单调性时,停止维护的情况为:栈空,遇到左括号以及满足了单调性
当遇到右括号时,我们需要不断进行eval运算,直达遇到左括号eval运算停止,最后将左括号出栈
#include 829. 模拟队列
#include 830. 单调栈
#include 154. 滑动窗口
代码中检测当窗口左侧所在的位置是否在当前窗口左侧应该在的位置,以此判断是否要更新窗口
#include kmp练习题
831. KMP字符串
#include