RFID课程要点总结_4 Tag Identification Protocol

4. Tag Identification Protocol

Checksum procedure: parity checks, LRC, CRC

奇偶校验不多说，查1的个数，poor error recognition。电路通过所有位异或是偶校验，结果为1说明有错误；再取反是奇校验。

LRC longitudinal redundancy check (LRC) procedure 循环冗余检测，所有字节进行异或运算，得到的结果是LRC校验码。也就是说数据发送到终点后，所有字节（数据和LRC）进行字节异或运算结果应该为0. 也有一些错误无法纠正，主要用于小的数据块校验。

CRC (cyclic redundancy check) procedure

接收方计算原数据+CRC数据拼接起来的CRC数据值，应该为0. 不能纠错，不过检错效率很高。

ASK, FSK, PSK

amplitude Shift Keying: 幅度调制，y轴上的调制。

计算方法2：duty factor: $m=1-\frac{u_1}{u_0}$

$U_{ASK}(t)=(m\cdot u_{code}(t)+1-m)\cdot u_{HF}(t)$

Frequency shift keying: 频率上的改变。

Phase shift keying: 频率相位翻转180.

Difficulty of traditional anti-collision algorithms for solving collision detection between RFID tags

Compared with the reader, limited by hardware resources, tags have very limited storage capacity and computing.

标签受制于硬件资源，存储容量和计算能力都不高。

TDMA, FDMA, CSMA

首先主要有两种方式，一个是reader broadcast 广播到诸多 tags，一个是多个 tags Multi-access 每个tags单独访问reader。

TDMA FDMA是multi-access, CSMA是broadcast

FDMA: 多个频率通道 several frequency channels 传输数据。

TDMA:

ALOHA based protocols: pure ALOHA, S-ALOHA, FSA, DFSA, Q 算法。重点：性能分析、执行过程

Pure ALOHA algorithm：收到成功确认 ack 后就不再发送。否则一直随机等待后继续发送。简单但是通道利用率 channel utilization 低，poor performance.

offered load G：单位时间 tau 里同时发送的应答器数量

s-aloha: 规定时间片 slot，一个时间片只能发一次，冲突就下一次时间片去发。channel utilization 几乎是 pure 的两倍。

$S=G\times e^{-G}$ G=1最大

frame S-ALOHA: 规定一个周期 frame，包含若干个 slots，会更加有组织有秩序。reader 广播一个 frame length，tags 自己选择组织时间片（0~f-1），每个时间片开始 reader 轮询一下tag里sn信号是不是0，是0就发送，不是0就-1.

conflict slot, single slot, idle slot（空）

逻辑，电路设计，内存都比较简单，但是 frame length 长度不固定。tags 远远多于 frame length 冲突时间片就太多，tags 太少空时间片太多太浪费。负载 G=1 也就是 length=tags 利用率最好。

DFSA：利用以前的 frame 冲突反馈结果，和一些机器学习算法推测合适的 frame length。

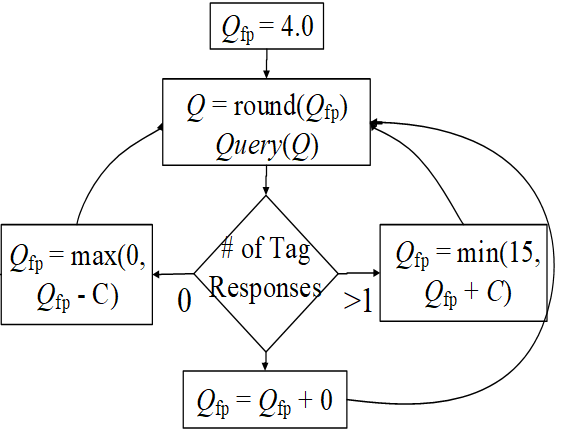
EPC Global（第五章介绍）规范里使用了一种Q算法。简单说就是如果冲突太多了，当前 frame 就别继续了，中断，新开一个大容量 frame. 同理 空闲太多了就新开一个小 frame。

Qfp是指定的初始值。每次先取整，然后发起 query。

没有回复：Qfp-C C是一个参数，比如0.1.

有冲突>1：+C。注意有上下限。

ALOHA 算法公平。但是可能发生饥饿 ，比如有一个 tag 每次都是有冲突的 slot，一直没有办法被处理。

Binary tree based protocols: BT, QT, 重点：执行过程

第二种算法，基于二进制数。就像二叉树不断拆分冲突的结点变为两个结点，直到节点里只有一个 tag。

random binary tree BT：随机。

binary query tree QT：排序，查询。

每一个 tag 需要有一个计数器来记录自己的状态。

每一个tag都会被识别，不会饥饿，但是需要存储每个tag的状态。

比如看下面的例子：

首先 tag1234 随机选一个数，比如选了0010，SN分别加自己选的数。

找SN=0的，发现有是有，但是他们几个都冲突了。那么继续分，比如1011，SN=1021

2的SN=0而且不冲突，把2读取了之后2不再继续参与。然后当有tag读取后，所有其他SN-=1

=0的是14，但是他俩冲突。然后再重新划分一下，比如011, SN=0021

然后处理1，其他-=1，处理4，其他-=1，处理3.

QT 不需要存储状态，如何实现？读取tag的序列号比较。

不会饿死，也不需要一个可以读写的cnt，识别的时间和 tag id 有关。

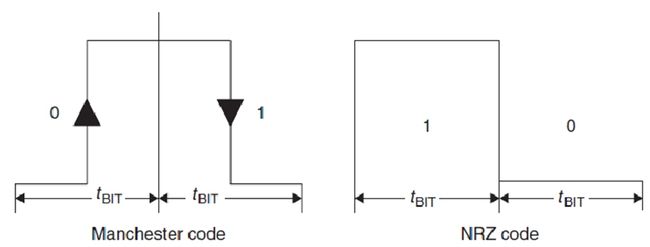
Binary search: Manchester code instead of NRZ code, 重点：执行过程

具体分辨哪一位有冲突。1代表冲突。

NRZ混合没法检测错误。

曼彻斯特可以，一个上升一个下降，合起来是0或者1.

查询的流程：

• request：发送一个序列号给tags的transponder，如果tags的序列号小于给定序列号返回。
• select：给定一个特定序列号，返回等序列号的tag。
• read_data：返回所选tag的信息。
• unselect：读取完data了，这个tag退出选择流程。

第一次迭代：返回uplink是所有transponder的id的共同信息（通过曼彻斯特编码找出没有冲突的位）。046位冲突了（从右往左），8个可能。

第二次迭代：限定 bit6 为0的request。发现有3个还是冲突04位（最高位冲突位=0，其他冲突位=1，如果range是大于等于，则正好相反）。

第三次迭代：限定bit4为0的request……

长度 L(N)=log2(N)+1

Dynamic binary search, 重点：执行过程

Binary Search 是每次都传输完整二进制字符串. 其实我们只需要动态改变的部分.

比如我们查询1010 1111 1111, 那返回值前面一定是1010呀, 就不用传输了. 前缀叫 NVB, Number of Valid Bits

每次请求发送的信息: Request+NVB=4+1010

Advantages and disadvantages of ALOHA based anti-collision algorithm

simple

good identification performance

results can be statistically analyzed 结果可以被统计化分析

缺点就是可能 starvation 饥饿，delay trend to ∞

Advantages and disadvantages of binary tree based anti-collision algorithm

simple

intermediate state variables 不需要存储中间状态变量（QT）

缺点：查询时间受到 tags id 和 长度限制，比如二叉树沿着一个方向一直偏。