【tushare使用经验分享】等权重模型、均值方差模型、风险平价模型的投资组合配置比较

id:472745

获取2015.1.1至2021.12.31期间 贵州茅台、美的集团、宁波银行、中国平安、三一重工 五只股票的日度收益数据。 利用2015.1.1—2019.12.31间的数据作为训练样本，并分别利用以下三种模型构造投资组合：（1）等权重；（2）哈利马科维兹（M-V）模型；（3）风险平价模型。 试比较以上三种投资组合在 2020.1.1—2021.12.31之间的表现。

##模块导入
import datetime
import time
from datetime import timedelta
from dateutil.relativedelta import *
import statsmodels.api as sm
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas import DataFrame, Series
import math
import tushare as ts
token='xxx'
ts.set_token(token)
pro=ts.pro_api()
import ffn
%matplotlib inline

一、提取五只股票日度收益率数据

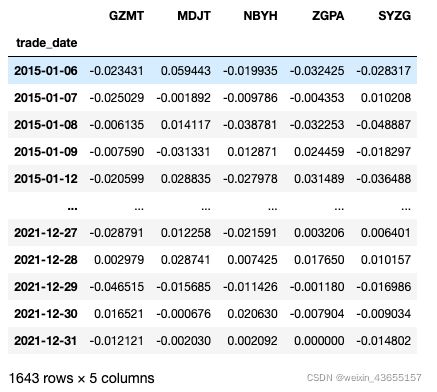
#提取各只股票的日度收益率数据（前复权）
df_gzmt=ts.pro_bar(ts_code='600519.SH',     adj='qfq',start_date='20150101',end_date='20211231').set_index(['trade_date']).sort_index()
df_mdjt=ts.pro_bar(ts_code='000333.SZ', adj='qfq',start_date='20150101',end_date='20211231').set_index(['trade_date']).sort_index()
df_nbyh=ts.pro_bar(ts_code='002142.SZ', adj='qfq',start_date='20150101',end_date='20211231').set_index(['trade_date']).sort_index()
df_zgpa=ts.pro_bar(ts_code='601318.SH', adj='qfq',start_date='20150101',end_date='20211231').set_index(['trade_date']).sort_index()
df_syzg=ts.pro_bar(ts_code='600031.SH', adj='qfq',start_date='20150101',end_date='20211231').set_index(['trade_date']).sort_index()
#将数据存入dataframe中
data=pd.DataFrame({'GZMT':ffn.to_log_returns(df_gzmt['close']),
                 'MDJT':ffn.to_log_returns(df_mdjt['close']),
                 'NBYH':ffn.to_log_returns(df_nbyh['close']),
                 'ZGPA':ffn.to_log_returns(df_zgpa['close']),
                 'SYZG':ffn.to_log_returns(df_syzg['close'])})
data=data.dropna()
data.index=pd.to_datetime(data.index)
data.describe()
data

#绘制收益率折线图
data.plot(figsize=(12,6),grid=True)
#绘制累积收益率折线图
cumreturn=(1+data).cumprod()
cumreturn.plot(figsize=(12,6),grid=True)

data.corr()#各只股票的相关系数相关系数
#划分训练集与测试集
train_set=data.loc['2015':'2019']
test_set=data.loc['2020':'2021']

二、构建模型

1、均值方差模型 

#构建均值方差模型
def M_V(R, rf, Sigma, output_type = 'Dict', print_out = False):
    '''
    :param R: list格式，输入各收益序列
    :param rf: num格式或list格式，输入无风险利率
    :param Sigma: two-d list格式，输入各收益序列协方差矩阵
    :param output_type: Bool类型，True为打印结果，Flase为不打印结果
    :param : num格式或list格式
    :return: dataframe
    '''
    
    # Step 1: 初始化收入变量格式
    N = len(R) # 获取资产类别数
    R = np.array(R).reshape(N) # 格式化收益率序列
    rf = np.array(rf) # 格式化无风险利率
    Sigma = np.array(Sigma).reshape(N, N) # 格式化协方差矩阵

    # Step 2: 利用minimize函数进行模型求解：
    eps = 1e-10  # 找到一个非常接近0的值作为误差限
    w0 = np.ones(N) / (N)  # 各类别资产权重参数初始化
    fun = lambda w:  - np.dot(w, R - rf) / np.dot(np.dot(w, Sigma), np.transpose(w))**0.5 # 约束函数：最大化对数sharpe-ratio
    cons = ({'type': 'eq', 'fun': lambda w: np.sum(w) - 1},  # 限制条件一：全部投资
            {'type': 'ineq', 'fun': lambda w: w - eps},  # 限制条件二：不可做空
            )
    res = minimize(fun, w0, method='SLSQP', constraints=cons)

    # Step 4: 计算各指标
    w_op = res.x # 获取权重数据
    r_op = np.dot(res.x, R) # 计算收益率
    sigma_op = np.dot(np.dot(w_op, Sigma), np.transpose(w_op)) # 计算组合波动率
    SR = (r_op - rf) / sigma_op # 计算夏普比率

    # Step 5: 是否打印测试
    if print_out:
        print('''
        最优权重配比：{0:}
        最优收益率：{1:.2f}
        最优风险：{2:.2f}
        最优夏普比率：{3:.2f}  
            '''.format(w_op, r_op, sigma_op, SR))
            
    # Step 6: 打印模块
    if str(output_type).upper() == 'DATAFRAME':
        return pd.DataFrame({'Weights':[w_op], 'Return':r_op, 'Sigma':sigma_op, 'SR':SR})
    elif str(output_type).upper() == 'DICT':
        return {'Weights':w_op, 'Return':r_op, 'Sigma':sigma_op, 'SR':SR}
    elif str(output_type).upper() == 'LIST':
        return [w_op, r_op, sigma_op, SR]
    else:
        return {'Weights':w_op, 'Return':r_op, 'Sigma':sigma_op, 'SR':SR}


def weights_calculate_MV(returns):
    weights_strategy_MV = []
    R = []
    for i in range(5):
        R.append(np.mean(returns[tickers[i]]))
   
    rf = np.mean(rff['rff']) 
    Sigma = np.cov(returns[tickers[0:5]], rowvar=False)
    outcome = M_V(R=R, rf=rf, Sigma=Sigma)
    weights_strategy_MV.append(outcome['Weights'])

    return weights_strategy_MV

2、风险平价模型

#构建风险平价模型
def R_P(R, rf, Sigma, output_type = 'Dict', print_out = False):
    '''
    :param R: list格式，输入各收益序列
    :param rf: num格式或list格式，输入无风险利率
    :param Sigma: two-d list格式，输入各收益序列协方差矩阵
    :param output_type: Bool类型，True为打印结果，Flase为不打印结果
    :param : num格式或list格式
    :return: dataframe
    '''
    
    # Step 1: 初始化收入变量格式
    N = len(R) # 获取资产类别数
    R = np.array(R).reshape(N) # 格式化收益率序列
    rf = np.array(rf) # 格式化无风险利率
    Sigma = np.array(Sigma).reshape(N, N) # 格式化协方差矩阵

    # Step 2: 利用minimize函数进行模型求解：
    eps = 1e-10  # 找到一个非常接近0的值作为误差限
    w0 = np.ones(N) / N  # 各类别资产权重参数初始化
    fun = lambda w: np.dot(w - np.dot(np.dot(w, Sigma), np.transpose(w))/N / np.dot(w, Sigma),
                           np.transpose(w - np.dot(np.dot(w, Sigma), np.transpose(w))/N / np.dot(w, Sigma) ))

    cons = ({'type': 'eq', 'fun': lambda w: np.sum(w) - 1},  # 限制条件一：全部投资
            {'type': 'ineq', 'fun': lambda w: w - eps},  # 限制条件二：不可做空
            )
    res = minimize(fun, w0, method='SLSQP', constraints=cons)

    # Step 4: 计算各指标
    w_op = res.x # 获取权重数据
    r_op = np.dot(res.x, R) # 计算收益率
    sigma_op = np.dot(np.dot(w_op, Sigma), np.transpose(w_op)) # 计算组合波动率
    SR = (r_op - rf) / sigma_op # 计算夏普比率

    # Step 5: 是否打印测试
    if print_out:
        print('''
        最优权重配比：{0:}
        最优收益率：{1:.2f}
        最优风险：{2:.2f}
        最优夏普比率：{3:.2f}  
            '''.format(w_op, r_op, sigma_op, SR))

    # Step 6: 打印模块
    if str(output_type).upper() == 'DATAFRAME':
        return pd.DataFrame({'Weights':[w_op], 'Return':r_op, 'Sigma':sigma_op, 'SR':SR})
    elif str(output_type).upper() == 'DICT':
        return {'Weights':w_op, 'Return':r_op, 'Sigma':sigma_op, 'SR':SR}
    elif str(output_type).upper() == 'LIST':
        return [w_op, r_op, sigma_op, SR]
    else:
        return {'Weights':w_op, 'Return':r_op, 'Sigma':sigma_op, 'SR':SR}

def weights_calculate_RP(returns):
    weights_strategy_RP = []
    R = []
    for i in range(5):
        R.append(np.mean(returns[tickers[i]]))
    rf = np.mean(rff['rff']) 
    Sigma = np.cov(returns[tickers[0:5]], rowvar=False)
    outcome = R_P(R=R, rf=rf, Sigma=Sigma)
    weights_strategy_RP.append(outcome['Weights'])

    return weights_strategy_RP

3、均值模型

def weights_calculate_EW(returns):
    weights_strategy_EW = np.ones(5)/returns.shape[1]
    return weights_strategy_EW

三、计算组合权重

tickers = ["GZMT","MDJT","NBYH","ZGPA","SYZG"]
td_dates = train_set.index #记录交易日信息，方便以后进行查找
ts_dates = test_set.index
n = len(td_dates)
rff= pd.DataFrame(np.ones((n,1))*0.003, index = td_dates, columns =['rff'])

nv_strategy_EW= []
nv_strategy_MV= []
nv_strategy_RP= []
nv_strategy_EW = [1]
r_strategy_EW = []
nv_strategy_MV = [1]
r_strategy_MV = []
nv_strategy_RP = [1]
r_strategy_RP = []

returns=train_set # 设置训练日期
returns_test=test_set #设置测试日期
weights_strategy_EW = weights_calculate_EW(returns) # 计算等权重策略权重序列
weights_strategy_MV = weights_calculate_MV(returns) # 计算马科维茨模型策略权重序列
weights_strategy_RP = weights_calculate_RP(returns) # 计算风险平价策略权重序列

data_weight={"weights_strategy_EW":weights_strategy_EW,
           "weights_strategy_MV":weights_strategy_MV[0],
           "weights_strategy_RP":weights_strategy_RP[0]}
df_weight=pd.DataFrame(data_weight,index=['GZMT','MDJT','NBYH','ZGPA','SYZG'])
df_weight

for i in range(len(ts_dates)):
    r_strategy_EW.append(weights_strategy_EW[0] * returns_test[tickers[0]][ts_dates[i]] +
                         weights_strategy_EW[1] * returns_test[tickers[1]][ts_dates[i]] +
                         weights_strategy_EW[2] * returns_test[tickers[2]][ts_dates[i]] +
                         weights_strategy_EW[3] * returns_test[tickers[3]][ts_dates[i]] +
                         weights_strategy_EW[4] * returns_test[tickers[4]][ts_dates[i]])
    r_strategy_MV.append(weights_strategy_MV[0][0] * returns_test[tickers[0]][ts_dates[i]] +
                         weights_strategy_MV[0][1] * returns_test[tickers[1]][ts_dates[i]] +
                         weights_strategy_MV[0][2] * returns_test[tickers[2]][ts_dates[i]] +
                         weights_strategy_MV[0][3] * returns_test[tickers[3]][ts_dates[i]] +
                         weights_strategy_MV[0][4] * returns_test[tickers[4]][ts_dates[i]])
    r_strategy_RP.append(weights_strategy_RP[0][0] * returns_test[tickers[0]][ts_dates[i]] +
                         weights_strategy_RP[0][1] * returns_test[tickers[1]][ts_dates[i]] +
                         weights_strategy_RP[0][2] * returns_test[tickers[2]][ts_dates[i]] +
                         weights_strategy_RP[0][3] * returns_test[tickers[3]][ts_dates[i]] +
                         weights_strategy_RP[0][4] * returns_test[tickers[4]][ts_dates[i]])
    nv_strategy_EW.append(nv_strategy_EW[i] * (1 + r_strategy_EW[i]))
    nv_strategy_MV.append(nv_strategy_MV[i]* (1 + r_strategy_MV[i]))
    nv_strategy_RP.append(nv_strategy_RP[i] * (1 + r_strategy_RP[i]))

 四、进行模型回测

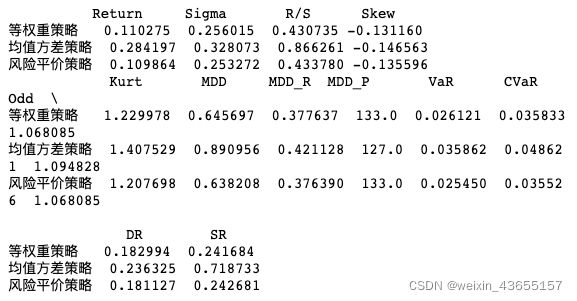
#Risk_Factor为导入文件
import Risk_Factor as RF
r_series = [r_strategy_EW ,r_strategy_MV , r_strategy_RP]
nv_series = [nv_strategy_EW ,nv_strategy_MV ,nv_strategy_RP]
 
Period = 'D'
Indicators = 'ALL'
alpha = 0.05
output_type = 'pd.DataFrame'
strategy_names = ['等权重策略', '均值方差策略', '风险平价策略']
rf=0.0002

# 进入风险值计算回测系统框架（该框架为自主创建，需要读取该文件）
Risks = RF.Risk_Indicators(r_series, nv_series,rf_series = rf, Period = Period, Indicators= Indicators, alpha=alpha, output_type=output_type)
Risks = pd.DataFrame(Risks.values.tolist(), index = strategy_names, columns = Risks.columns)

#打印风险值情况
print(Risks[Risks.columns[:4]])
print(Risks[Risks.columns[4:]])


nv_set=data.loc['2019-12-31':'2021']#横坐标提取
nv_index=nv_set.index
result_nv={"nv_strategy_EW":nv_strategy_EW,"nv_strategy_MV":nv_strategy_MV,"nv_strategy_RP":nv_strategy_RP}
result_nv_strategy=pd.DataFrame(result_nv, index= nv_index)

plt.figure(figsize=(12,6))
plt.grid()
plt.plot(result_nv_strategy['nv_strategy_EW'], label='nv_strategy_EW', color="red")
plt.plot(result_nv_strategy['nv_strategy_MV'], label='nv_strategy_MV', color="green")
plt.plot(result_nv_strategy['nv_strategy_RP'], label='nv_strategy_RP', color="yellow")
plt.legend(loc='best')