【数据结构-查找】树型查找

1 折半查找判定树

1.1 折半查找判定树的性质

1. 若指针 low 和 high 指向表的上界和下界，mid = (low+high)/2（向下取整，也是 C 语言除法运算的特性），则：

• 若 low 和 high 之间有奇数个元素，则 mid 的左右部分元素个数相等；
• 若 low 和 high 之间有偶数个元素，则 mid 的左半部分比右半部分元素个数少一个。

【例】若 low 和 high 之间有 10 个元素，则 mid = (low+high)/2 = (1+10)/2 = 11/2 = 5，所以 mid 的左半部分有 4 个元素，右半部分有 5 个元素。

2. 若指针 low 和 high 指向表的上界和下界，mid = (low+high)/2（向上取整，或按照 C 语言规则写成 (low+high)/2+1），则：

• 若 low 和 high 之间有奇数个元素，则 mid 的左右部分元素个数相等；
• 若 low 和 high 之间有偶数个元素，则 mid 的左半部分比右半部分元素个数多一个。

【例】若 low 和 high 之间有 10 个元素，则 mid = (low+high)/2 + 1 = (1+10)/2 + 1 = 11/2 + 1 = 6，所以 mid 的左半部分有 5 个元素，右半部分有 4 个元素。

【推论】在分块查找中，若对索引表进行向下取整的折半查找时，若索引表不包含目标关键字，则折半查找最终停在 low > high，要在 low 所指的分块查找；若对索引表进行向上取整的折半查找时，若索引表不包含目标关键字，则要在 high 所指的分块查找。

3. 任意两棵折半查找判定树，若取整方向一致，且它们的结点个数相同，则它们的结构完全相同。

【注】在 1.2 节判定树的画法中将体会到这一点。

4. 若折半查找判定树有 n 个结点，则失败结点（外部结点/空指针域）有 n+1 个。

【证明】判定树是一棵有 n 个结点的非空二叉树，设不同度的结点个数分别为 n₀、n₁、n₂，有n0 = n2 + 1，n = n0 + n1 + n2，将n2代入消去，得n = 2n0 + n1 - 1。注意到此时2n0 + n1即为空指针域的总数，因而总结点数比空指针域总数少 1。

5. 若折半查找判定树有 n 个结点，则树高（不包含失败结点）为log2(n+1)（向上取整）或log2n（向下取整）+1，即查找成功最多需要log2(n+1)（向上取整）次，时间复杂度为 O(log₂n)。

1.2 折半查找判定树的画法

向下取整的折半判定树的画法：

• 先画出最大的满二叉树；
• 从上往下看，比较每个结点的左右子树的结点个数，若个数相同则优先放右边，若左边比右边少则放左边。

向上取整的折半判定树的画法：

• 先画出最大的满二叉树；
• 从上往下看，比较每个结点的左右子树的结点个数，若个数相同则优先放左边，若右边比左边少则放右边。

【例】画出一棵共 12 个结点的查找判定树（向下取整）：

1.3 折半查找法的查找长度

• 通用公式：ASL = ∑(查找次数*概率)
• 查找成功公式：ASL（成功） = ∑(查找成功次数*概率)，其中概率 = 1/成功结点总数
• 查找失败公式：ASL（成功） = ∑(查找失败次数*概率)，其中概率 = 1/失败结点总数

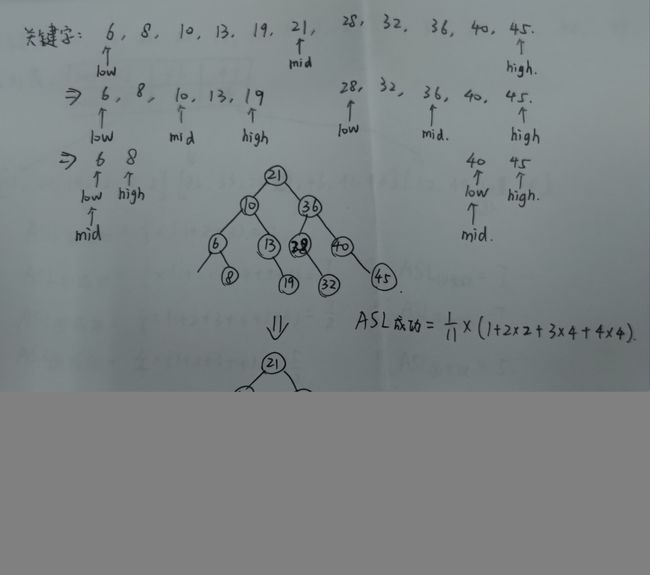
以上图为例：

• ASL（查找成功）= 1*1/12 + 2*2/12 + 3*4/12 + 4*5/12 = 37/12
• ASL（查找失败）= 3*3/13 + 4*10/13 = 49/13

1.4 相关例题

关键字：6,8,10,13,19,21,28,32,36,40,45

2 二叉排序树（BST）

2.1 二叉排序树的性质

1. 若二叉排序树有 n 个结点，则树高（不包含失败结点）为log2(n+1)（向上取整）或log2n（向下取整）+1，即查找成功最多需要log2(n+1)（向上取整）次，时间复杂度为 O(log₂n)。插入和删除操作的时间复杂度需要 O(n)。

2. 在二叉排序树中删除并插入某结点，得到的排序二叉树一般与原来不同。

3. 折半查找判定树唯一，但二叉排序树不唯一，其结构与关键字的插入顺序有关。

4. 假设以 n_h 表示深度为 h 的二叉平衡树中含有的最少结点数（可得到最大深度的二叉平衡树），则有 n₀ = 0，n₁ = 1，n₂ = 2，并且nh = nh-1 + nh-2 + 1。

2.2 二叉排序树的建立（代码）

#include 
using namespace std;

// 二叉树结点声明 
typedef struct TreeNode{
	TreeNode *left;
	TreeNode *right;
	int data;
	TreeNode (int x): left(NULL), right(NULL), data(x) {}
} TreeNode;

// 二叉排序树的建立 
TreeNode *insert (int x, TreeNode *root){
	if (root == NULL){
		root = new TreeNode(x);
	}
	else if (x < root->data){
		root->left = insert(x, root->left);
	}
	else{
		root->right = insert(x, root->right);
	}
	return root;
}

// 前序遍历 
void PreOrder (TreeNode *root){
	if (root != NULL){
		printf("%d ", root->data);
		PreOrder(root->left);
		PreOrder(root->right);
	}
}

// 中序遍历 
void InOrder (TreeNode *root){
	if (root != NULL){
		InOrder(root->left);
		printf("%d ", root->data);
		InOrder(root->right);
	}
}

// 后序遍历 
void PostOrder (TreeNode *root){
	if (root != NULL){
		PostOrder(root->left);
		PostOrder(root->right);
		printf("%d ", root->data);
	}
}

int main(){
	int n;
	TreeNode *T;
	
	while (scanf("%d", &n) != EOF){
		T = NULL;
		for (int i = 0; i < n; i++){
			int x;
			scanf("%d", &x);
			T = insert(x, T);
		}
		PreOrder(T); printf("\n");
		InOrder(T); printf("\n");
		PostOrder(T); printf("\n");
	}
	
	return 0;
}

2.3 二叉排序树的插入和删除

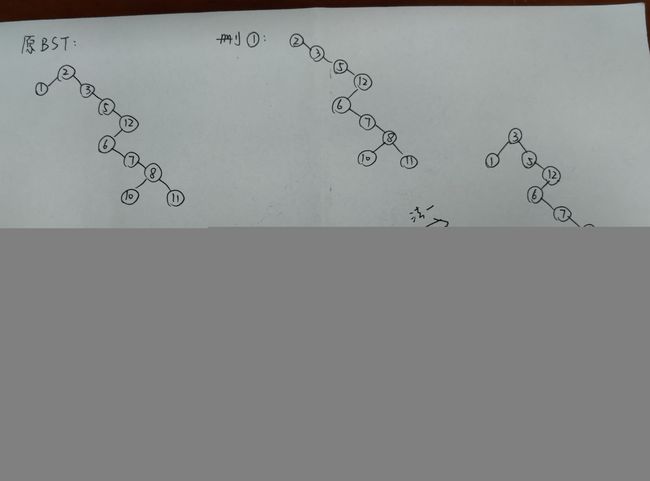
删除操作：可先将元素按序排列，然后找到待删除元素的左右两个元素，挑选任意一个元素替代这个待删除元素即可。

如上图：元素排好序后为 1,2,3,5,6,7,8,10,11,12，则删除元素 2，可选择元素 1 去替代它（法二），也可以选择元素 3 去替代它（法一）。

3 平衡二叉树（AVL）

3.1 平衡二叉树的性质

• 任何一个结点的左右两个子树的高度之差不超过 1，并且左右两个子树都是一棵平衡二叉树。
• 查找、插入和删除操作的时间复杂度需要 O(log₂n)。

3.2 平衡二叉树的旋转

3.2.1 基本操作——左旋、右旋

• 左旋：不平衡结点变为其右孩子的左孩子。
• 右旋：不平衡结点变为其左孩子的右孩子。

3.2.2 四种非平衡形态——LL、RR、LR、RL

• LL 型：结点 A 的左孩子（L）的左子树（L）插入了新结点，导致结点 A 失衡。解决办法：右旋一次。
• RR 型：结点 A 的右孩子（R）的右子树（R）插入了新结点，导致结点 A 失衡。解决办法：左旋一次。
• LR 型：结点 A 的左孩子（L）的右子树（R）插入了新结点，导致结点 A 失衡。解决办法：左旋一次，转化为 LL 型，再右旋一次。
• RL 型：结点 A 的右孩子（R）的左子树（L）插入了新结点，导致结点 A 失衡。解决办法：右旋一次，转化为 RR 型，再左旋一次。

【应试】简化流程

因为实际的二叉树形态很复杂，因此需要一个简便的方法用来快速解题（例子见下节）：

• 从最深的叶结点一路向上找到第一个失衡结点；
• 从这条路径上的失衡结点以及后面两个结点，组成了四种非平衡形态的一种；
• 先断开其他结点，把这三个结点按上面四种形态旋转，使其恢复平衡；
• 最后把断开的其他结点按照关系连回到正确位置上。

3.3 平衡二叉树的插入

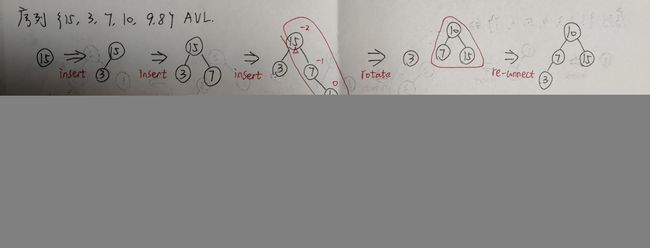
【例 1】插入序列 {15,3,7,10,9,8}

【例 2】插入序列 {1,2,3,4,5,6,7}

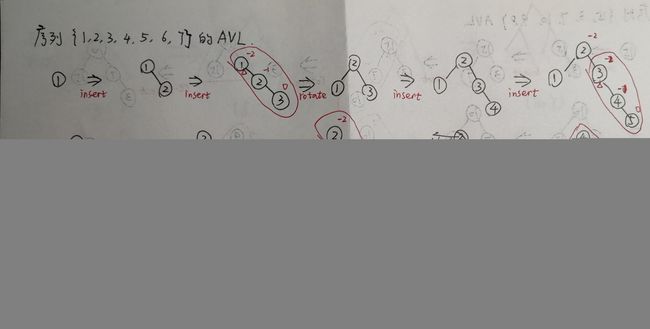
【例 3】插入序列 {2,1,5,3,8,9,10,11,4,7,6}

4 多路平衡查找树（B 树）

4.1 B 树的性质

假设一棵 m 阶 B 树，则满足以下特性：

1. 每个结点最多有 m 棵子树，最多含有 m-1 个关键字。

2. 根结点（如果它不是终端结点）至少有两棵子树。

3. 所有非叶结点（根结点除外）最少有┍m/2┑棵子树（即最少有 m 的一半过数这么多），最少含┍m/2┑-1个关键字。

【推论】结点的关键字个数范围为┍m/2┑-1 ≤ n ≤ m-1。

4. 设 B 树有 n 个关键字，则其高度范围为logm(n+1) ≤ h ≤ log┍m/2┑((n+1)/2) + 1。

【证明 1】结点最多（且每个结点含关键字数最多，高度最小）的情况：B 树每个结点最多有 m 棵子树、m-1 个关键字，所以关键字总数的范围为n ≤ (m-1)(1+m+m2+…+mh-1) = mh-1，反解出 h 的范围：logm(n+1) ≤ h。

【证明 2】结点最少（且每个结点含关键字数最少，高度最大）的情况：设k = ┍m/2┑，B 树每个结点最少有 k 棵子树、k-1 个关键字。第 1 层最少有 1 个结点，第 2 层至少有 2 个结点，第 3 层至少有 2k 个结点，第 4 层至少有 2k² 个结点，以此类推，第 h 层至少有 2k^h-2 个结点；因而，第 1 层最少有 1 个关键字，第 2 层至少有 2(k-1) 个关键字，第 3 层至少有 2k(k-1) 个关键字，第 4 层至少有 2k²(k-1) 个关键字，以此类推，第 h 层至少有 2k^h-2(k-1) 个关键字。所以，关键字总数的范围为n ≥ 1 + 2(k-1) + 2k(k-1) + 2k2(k-1) + … + 2kh-2(k-1) = 1 + (k-1)(1 + k + k2 + … + kh-2) = 1 + 2(kh-1 - 1)，反解出 h 的范围：h ≤ logk((n+1)/2) + 1 = log┍m/2┑((n+1)/2) + 1。

5. B+ 树可视为使用了分块查找的 B 树。

相关例题

【例 1】高度为 5 的 5 阶 B 树至少有几个结点和关键字？至多有几个结点和关键字？

【解】a. 结点最少的情况：根结点有 2 棵子树，其他非叶结点有 3 棵子树，设高度为 h，则结点总数为1 + 2 + 2*31 + 2*32 +…+ 2*3h-2 = 1 + 2 * (30 + 31 +…+ 3h-2) = 1 + 2 * 1/2 * (3h-1 - 1) = 3h-1，代入 h=5 得结点总数为 81。

b. 关键字最少的情况：在结点总数最少的情况下，根结点有 1 个关键字，其他非叶结点有 2 个关键字，设高度为 h，则关键字总数为1 + 2 * (2 + 2*31 + 2*32 +…+ 2*3h-2) = 1 + 4 * (30 + 31 +…+ 3h-2) = 1 + 4 * 1/2 * (3h-1 - 1) = 1 + 2 * (3h-1 - 1)，代入 h=5 得关键字总数为 161。

c. 结点最多的情况：所有结点都有 5 棵子树，设高度为 h，则结点总数为1 + 5 + 52 + 53 +…+ 5h-1 = 1/4 * (5h - 1)，代入 h=5 得结点总数为 781。

d. 关键字最多的情况：在结点总数最多的情况下，根结点和其他非叶结点有 4 个关键字，设高度为 h，则关键字总数为4 * (1 + 5 + 52 + 53 +…+ 5h-1) = 5h - 1，代入 h=5 得关键字总数为 3124。

【例 2】一棵 3 阶 B 树中有 2047 个关键字，则此 B 树的最大高度是多少？最小高度是多少？

【解】a. 最大高度：即结点总数和关键字总数都是最少的情况，根结点有 2 棵子树（1 个关键字），其他非叶结点有 2 棵子树（1 个关键字）。则关键字总数为1 * (1 + 2 + 22 + 23 +…+ 2h-1) = 2h - 1 = 2047，解得 h=11。

b. 最小高度：即结点总数和关键字总数都是最多的情况，所有结点都有 3 棵子树（2 个关键字）。则关键字总数为2 * (1 + 3 + 32 + 33 +…+ 3h-1) = 2 * (3h - 1) = 2047，解得 h=7。

【例 3（变形）】在一棵有 15 个关键字的 4 阶 B 树中，含关键字的结点个数最多几个？

【解】因为题目所求的是最多的结点数量，所以在关键字总数一定（15 个）的情况下，让每个结点都存储最少的关键字数。即根结点有 1 个关键字，其他非叶结点有 1 个关键字，推出每个非叶结点有 2 棵子树。因此关键字总数为1 * (1 + 2 + 22 + 23 +…+ 2h-1) = 1 * (2h - 1) = 2h - 1 = 15，解得 h=4。易知，含关键字的结点有 15 个。

【例 4（变形）】在一棵高度为 2 的 5 阶 B 树中，所含关键字的个数至少几个？

【解】因为题目所求的是最少的关键字总数，所以在高度一定的情况下，要求结点数最少，且每个结点所含关键字尽可能的少。因此，根结点有 1 个关键字，2 棵子树；其他非叶结点有 2 个关键字。因为高度为 2，所以第一层是根结点，第二层是两个非叶结点，关键字总数为 1+2*2=5。

4.2 B 树的插入和删除

相关例题

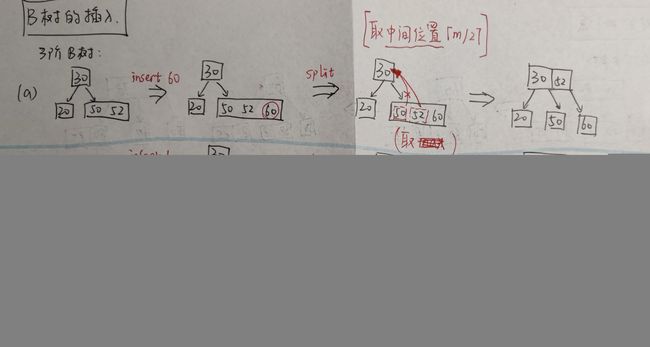
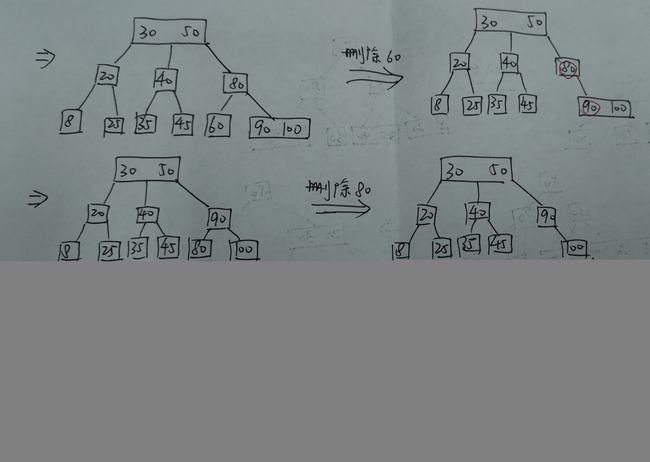
一棵 3 阶 B 树，插入 90、插入 25、插入 45、删除 60、删除 80：

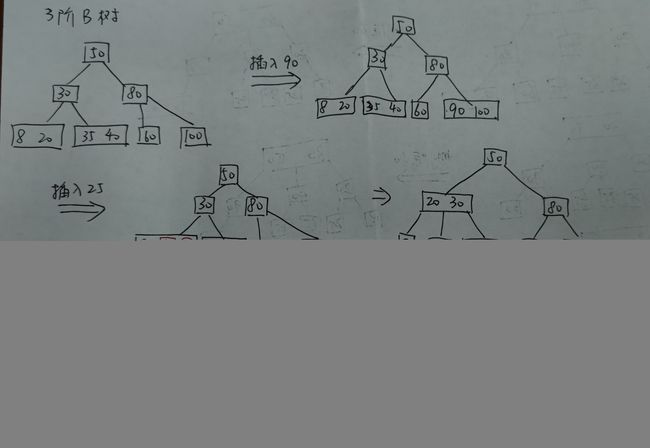
5 红黑树

（略）

---EOF---