C++矩陈操作类(好像求逆矩陈要用方程,下次完善解方程)
不完善,是因为自动解方程类的类比较复杂,还没写出来,卡在求逆矩陈函中。
例子:
#include "X:\Work\Share\CCode\CPlatform\AM\_Matrix.h"
#include "X:\Work\Share\CCode\CPlatform\AM\_Expression.h"
using namespace lf;
void main()
{
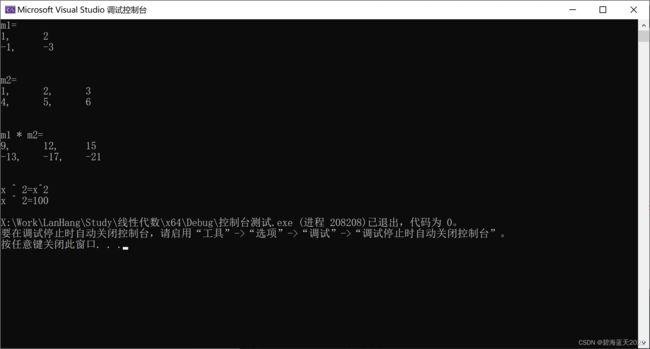
_Matrix m1(2, 2, { 1,2,-1,-3 });
_Matrix m2(2, 3, { 1,2,3,4,5,6 });
_pcn(m1);
_pcn(m2);
_pcn(m1 * m2);
_UnknownVar x(_t("x"));
//x^2 - 2x + 1 = 0
_pcn(x ^ 2);
x = 10;
_pcn(x ^ 2);
} 输出:
矩陈操作类:
_NDimensionalVectorSpace 用一维数组表示N维矩陈(前面用Java发表过,依照那时的思路)
_Matrix.h
/*******************************************************************************************
文件名 : _Matrix.h
作者 : 李锋
功能 : 线性代数(矩陈)
创建时间 : 2023-04-23
最后一次修改时间 : 2023-04-23
定义1.1:由n个a1,a2...an 数组成的一个有序数值称为一个n维向量,数ai 称为该n维向量的第i个分量。
若该向量表示成{ 一列,称为n维列向量,它也就是矩阵;若该向量表示成一行,称为n维行向量,它也就是矩阵。
********************************************************************************************/
#ifndef __MATRIX_H_
#define __MATRIX_H_
#include "_Equation.h"
_LF_BEGIN_
///
/// 前置声明
///
///
class _Matrix;
///
/// N维数组,n-维向量空间(n-dimensional vector space),在解析几何中有些事物的性质不能用一个数来刻画,
/// 如一个n元方程组的解是由n个数组成,而这n个数作为方程组的解是一个整体,分开来谈是没有意义的,这时我们
/// 就需要用n维向量来刻画方程组的解。在几何上这样的例子是很多的,所以n维向量在抽象代数这一领域的研究中起
/// 着很重要的作用。
///
///
class _NDimensionalVectorSpace : public _Object
{
protected:
///
/// 数域p (a1,a2,...,an)
/// 定义:一个n维向量空间就是由数域p中n个数组成的有序数组
/// (a1,a2,...,an),ai称为上述向量的一个分量。
///
_Array _NumberField;
///
/// 保存维度的数组
///
_Array _Dimensional;
public:
///
/// 获取向量空间的数域
///
__declspec(property(get = GetNumberField)) const _Array& NumberField;
///
/// 获取向量空间的数域
///
inline const _Array& GetNumberField() const { return _NumberField; }
///
/// 获取向量空间的维度数组
///
__declspec(property(get = GetDimensional)) const _Array& Dimensional;
///
/// 获取向量空间的维度数组
///
const _Array& GetDimensional() const { return this->_Dimensional; }
///
/// 获取向量空间的维度
///
__declspec(property(get = GetDimensionalCount)) const int DimensionalCount;
///
/// 获取向量空间的维度
///
inline int GetDimensionalCount() const { return _Dimensional.Length; }
inline _NDimensionalVectorSpace() { }
inline _NDimensionalVectorSpace(const _NDimensionalVectorSpace& ndvs)
{
_Dimensional = ndvs._Dimensional;
_NumberField = ndvs._NumberField;
}
///
///
///
///
/// 创建时间:2023-05-01 最后一次修改时间:2023-05-01
inline _NDimensionalVectorSpace(const _Array& arrDimensional)
{
_Dimensional = arrDimensional;
int nLength = 1;
for (int i = 0; i < arrDimensional.Length; ++i)
{
nLength *= arrDimensional[i];
}
_NumberField.SetBuffer(nLength);
for (int i = 0; i < nLength; ++i)
{
_NumberField.Add(T());
}
}
inline _NDimensionalVectorSpace(const _Array& arrDimensional, const _Array& arrNumberField)
{
_Dimensional = arrDimensional;
_NumberField = arrNumberField;
}
///
/// 如果 维向量 a=(a1,a2,...,an) b = (b1,b2,...,bn)
/// 的对应分量都相等,即 a1 = b1, a2 = b2, ... an = bn,
/// 就称这两个向量是相等的,记作 a = b;
///
///
/// & rhs)
{
if (this == &rhs) return true;
return _Dimensional == rhs._Dimensional && _NumberField == rhs._NumberField;
}
///
///
///
///
/// & rhs)
{
//_cout << _t("inline bool operator!=(const _NDimensionalVectorSpace& rhs)");
return !(*this == rhs);
}
///
/// 定义:
/// a = a=(a1,a2,...,an) b = (b1,b2,...,bn)
/// a + b = (a1+b1,a2+b2,...,an+bn)
///
///
/// operator+(const _NDimensionalVectorSpace& rhs)
{
//丙个n维向量的分量个数必须相等
assert(_Dimensional.Length == rhs._Dimensional.Length);
_NDimensionalVectorSpace ndvsResult;
_Array tmp = _NumberField;
for (int i = 0; i < tmp.Length; ++i)
{
tmp[i] += rhs._NumberField[i];
}
return _NDimensionalVectorSpace(_Dimensional, tmp);
}
///
/// 定义4:
/// 分量全为零的向量称为零向量,记为(0,0,...,0) ;向量(-a1,-a2,...,-an) 称为向量 a= (a1,a2,...,an) 的负向量,记为 -a。
/// 显然,对于所有的a,都有
/// a + 0 = a a + -a = 0
/// 利用负向量,可以定义向量的减法 a - b = a + (-b)
///
///
/// operator-(const _NDimensionalVectorSpace& rhs)
{
//丙个n维向量的分量个数必须相等
assert(_Dimensional.Length == rhs._Dimensional.Length);
_NDimensionalVectorSpace ndvsResult;
_Array tmp = _NumberField;
for (int i = 0; i < tmp.Length; ++i)
{
tmp[i] -= rhs._NumberField[i];
}
return _NDimensionalVectorSpace(_Dimensional, tmp);
}
///
/// 定义5:
/// 设 k 为数域 p 中的数,向量(ka1,ka2...kan) 称为向量 a = (a1,a2,...an) 与数 k 的数量乘积,记为 ka
///
///
/// operator*(const int& k, const _NDimensionalVectorSpace& ndvs)
{
_NDimensionalVectorSpace ndvsResult;
_Array tmp = ndvs._NumberField;
for (int i = 0; i < tmp.Length; ++i)
{
tmp[i] *= k;
}
return _NDimensionalVectorSpace(ndvs._Dimensional, tmp);
}
///
/// 定义5:
/// 设 k 为数域 p 中的数,向量(ka1,ka2...kan) 称为向量 a = (a1,a2,...an) 与数 k 的数量乘积,记为 ka
///
///
/// operator*(const _NDimensionalVectorSpace& ndvs, const int& k)
{
return k * ndvs;
}
///
///
///
/// dimensionValueArgs)const
{
/*
三维数组 a[3][2][5] => 用一维数字 m_DataArray[3*2*5] 表示。
假设三维数组 a[3][2][5] 3行2列5面数组 用 a[x_max][y_max][z_max] 代替,
那么 x_max = 3, y_max = 2, z_max = 5,那么
数组 m_DimensionMax = {x_max,y_max,z_max}
即:
dimensionValueArgi[0] = x_max = 3
dimensionValueArgi[1] = y_max = 2
dimensionValueArgi[1] = z_max = 5
所有元素可以看作 三个数列相加,数列名为 a[0],a[1],a[2]
a[0] 总数 10个
a[1] 总数 10个
a[2] 总数 10个
例子:getFixedPsition(0,1,2) x,y,z
第一列第一个无素是: a[0][0][0] => (y+1) * (z+1) => m_DataArray[ (x * y_max * z_max) + y+1) * (z+1) - 1] => m_DataArray[0]
第二列第一个元素是: a[1][0][0] => m_DataArray[ (x * y_max * z_max) + (y+1) * (z+1) - 1]
=> a[ ( 1 * 2 * 5) + (0+1) * (0+1) ] => m_DataArray[10];
错:
第二列第二个元素是: a[1][1][0] => m_DataArray[ ( x * y_max * z_max) + (y+1) * (z+1) - 1]
=> a[ ( 1 * 2 * 5) + (1+1) * (0+1) - 1] => m_DataArray[11];
错误: 计算结果是:m_DataArray[11],正确是 m_DataArray[16] = 11 + 5
最后:
a[x][y][z] => m_DataArray[ (x * y_max * z_max) + (y+1) * (z+1) - 1]
=> m_DataArray[ (dimensionValueArgi[0] * y_max * z_max) + ( dimensionValueArgi[1] + 1) * (dimensionValueArgi[2] + 1) - 1]
*/
/*
//时间问题,太晚了,这一版本暂时不进行异常处理
int i数列总数 = 1;
for(int i = 1; i < m_DimensionMax.length; ++i) {
i数列总数 *= m_DimensionMax[i];
}
int sum1 = dimensionValueArgi[0] * i数列总数;
int sum2 = 1;
for(int i = 1; i < dimensionValueArgi.length; ++i) {
sum2 *= (1 + dimensionValueArgi[i]);
}
return sum1 + sum2 - 1;
*/
int sum = 0;
for (int i = dimensionValueArgs.Length - 1; i >= 0; --i)
{
int n = 1;
for (int j = i + 1; j < _Dimensional.Length; j++)
{
n *= _Dimensional[j];
}
sum += n * dimensionValueArgs[i];
}
return sum;
}
///
/// 功能: 根据一维数组的索引,获取N维数组的坐标。
///
/// 索引
/// 返回坐标
/// 创建时间:2023-09-17 最后一次修改时间:2023-09-17
_Array GetCoordinateFromIndex(int nIndex)const
{
_Array iResultArray(_Dimensional.Length);
for (int i = 0; i < _Dimensional.Length; ++i)
{
iResultArray.Add(0);
}
int tmp = nIndex;
for (int i = 0; i < _Dimensional.Length; ++i) {
int sum = 1;
for (int j = i + 1; j < _Dimensional.Length; ++j) {
sum *= _Dimensional[j];
}
iResultArray[i] = tmp / sum;
tmp = tmp - sum * iResultArray[i];
}
return iResultArray;
}
/**
* 功能: 描述
* @param value
* @param dimensionValueArgi
* @return void
* @since 创建日期:2022年9月14日,最后一次修改日期:2022年9月14日
* @author 李锋
*/
void SetValue(const T& value, const _Array& dimensionValueArgi) {
//jp.p("getPsition(dimensionValueArgi)=" + getPsition(dimensionValueArgi) + "x=" + dimensionValueArgi[1] + ",y=" +
// dimensionValueArgi[2]);
//时间问题,太晚了,这一版本暂时不进行异常处理
_NumberField[GetIndexFromCoordinate(dimensionValueArgi)] = value;
}
/**
* 功能: 在区间[iMin,iMax]中的随机整数
* @param iMin
* @param iMax
* @return void
* @since 创建日期:2022年9月17日,最后一次修改日期:2022年9月17日
*/
void SetRandomInt(int iMin, int iMax) {
//for (int i = 0; i < m_DataArray.length; ++i) {
// m_DataArray[i] = jp.getRandomInt(iMin, iMax);
//}
}
///
/// 返回向量空间中坐标的元素引用
///
/// 坐标
/// & arrCoordinate)const
{
return _NumberField[GetIndexFromCoordinate(arrCoordinate)];
}
/**
* 功能: 维度数组转置
* If A is the mxn matrix, then the nxm matrix is called the transpose of A.
* 如果A是mxn矩阵, 那么nxm矩阵为A的转置矩阵.
* @return
* @since 创建日期:2022-09-16,最后一次修改日期:2022-09-16
* @author 李锋
* @throws Exception
*/
///
/// 参考: https://baike.baidu.com/item/%E8%BD%AC%E7%BD%AE%E7%9F%A9%E9%98%B5/3380917?fr=aladdin
/// 功能:返回一个转置矩阵
/// 转置矩阵定义:
/// 将矩阵的行列互换得到的新矩阵称为转置矩阵,转置矩阵的行列式不变。
/// 由定义可知,A[n,m] 转置后为 B[m,n]
///
/// Transposition() const
{
/*
二维数组:
8,4,5,7
9,3,9,9
1,6,4,6
转置后应该是:
8,9,1
4,3,6
5,9,4,
7,9,6
//二维
NDimensionalArray_ tmp = new NDimensionalArray_(Math_.copyReverseArray(m_DimensionMax));
if(m_DimensionMax.length == 2) {
for(int i = 0; i< m_DimensionMax[0]; ++i) {
for(int j = 0; j < m_DimensionMax[1]; ++j) {
tmp.setValue(getValue(i,j),j,i);
}
}
m_DataArray = tmp.m_DataArray;
m_DimensionMax = tmp.m_DimensionMax;
}
*/
//N维呢?探索中
//可以推导出
//N维数组转置原理:
//假设有 a1,a2,a3...an 维数组NDimensiona1,它转置后就是: an...a3,a2,a2
//转置后的关系一定有: NDimensiona1[a1,a2,a3...an] = NDimensiona2[an...a3,a2,a1]
_NDimensionalVectorSpace ndtvtResult(_Dimensional.Reverse());
for (int i = 0; i < _NumberField.Length; ++i)
{
T value = _NumberField[i];
_Array Coordinat = GetCoordinateFromIndex(i);
ndtvtResult.SetValue(value, Coordinat.Reverse());
}
return ndtvtResult;
}
};
///
/// 字符串表示的矩陈
///
class _MatrixS : public _NDimensionalVectorSpace<_string>
{
public:
/*
///
/// 获取向量空间的数域
///
__declspec(property(get = GetNumberField)) const _Array<_string>& NumberField;
///
/// 获取向量空间的数域
///
inline const _Array<_string>& GetNumberField() const { return _NumberField; }
*/
///
/// 行数
///
__declspec(property(get = GetRowsCount)) const int RowsCount;
inline int GetRowsCount()const { return this->_Dimensional[0]; }
///
/// 列数
///
__declspec(property(get = GetColumnsCount)) const int ColumnsCount;
inline int GetColumnsCount()const { return this->_Dimensional[1]; }
public:
_MatrixS();
_MatrixS(const int mRow, const int nColumn, bool bVariable = true);
_MatrixS(const _Matrix& intM);
virtual _string ToString() const override;
///
/// 矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时
/// 才有意义[1] 。一般单指矩阵乘积时,指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。
/// 由于它把许多数据紧凑地集中到了一起,所以有时候可以简便地表示一些复杂的模型,如电力系统网络模型。
///
/// 注意事项编辑 播报
/// 1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
/// 2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
/// 3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
///
///
///
///
/// 返回向量空间中坐标的元素引用
///
/// 坐标
///
/// 设置两个相等距陈元素相等的等式
///
///
void SetEquality(const _Matrix& intM);
};
///
/// 矩陈(由 m * n 个数 a[i,j] (i = 1,2,...,m, j = 1,2,...,n)排成 m 行,n列的数表称为 m 行 n 列 距陈
///
/// 创建时间:2023-04-27 最后一次修改时间:2023-04-27
template
class _Matrix : public _NDimensionalVectorSpace
{
public:
///
/// 行数
///
__declspec(property(get = GetRowsCount)) const int RowsCount;
inline int GetRowsCount()const { return this->_Dimensional[0]; }
///
/// 列数
///
__declspec(property(get = GetColumnsCount)) const int ColumnsCount;
inline int GetColumnsCount()const { return this->_Dimensional[1]; }
inline _Matrix() {}
///
/// 创建一个 m 行 n 列矩陈,且对所有元素初化为 T()
///
///
///
/// 创建时间:2023-04-27 最后一次修改时间:2023-04-29
inline _Matrix(const int mRow, const int nColumn)
{
assert(mRow >= 0 && nColumn >= 0);
this->_Dimensional = { mRow, nColumn };
for (int i = 0; i < mRow * nColumn; ++i)
{
this->_NumberField.Add(T());
}
}
///
/// 创建一个 m 行 n 列矩陈,其元素列表为arrElements
///
///
///
///
/// 创建时间:2023-04-27 最后一次修改时间:2023-04-29
inline _Matrix(const int mRow, const int nColumn, const _Array& arrElements)
{
assert(mRow >= 0 && nColumn >= 0);
assert(mRow * nColumn == arrElements.Length);
this->_Dimensional = { mRow, nColumn };
this->_NumberField = arrElements;
}
///
///
///
///
/// 创建时间:2023-05-01 最后一次修改时间:2023-05-01
inline _Matrix(const _Matrix& m)
{
this->_Dimensional = m._Dimensional;
this->_NumberField = m._NumberField;
}
inline _Matrix(const _NDimensionalVectorSpace& m)
{
assert(m.Dimensional.Length == 2);
this->_Dimensional = m.Dimensional;
this->_NumberField = m.NumberField;
}
///
/// 只有两个距陈是同型距陈时才可以进行加减法。
/// https://jingyan.baidu.com/article/6525d4b186fd4cac7c2e946f.html
///
///
/// operator+(const _Matrix& rhs)
{
//(1)距陈的维度都是2
//(2)元素个数必须相同
//(3)必须是同型距陈(距陈A和B的行数和列数都相等)
assert(this->_Dimensional.Length == rhs._Dimensional.Length && this->_Dimensional.Length == 2);
assert(this->_Dimensional[0] == rhs._Dimensional[0] && this->_Dimensional[1] == rhs._Dimensional[1]);
assert(this->_NumberField.Length == rhs._NumberField.Length);
_Array tmp = this->_NumberField;
for (int i = 0; i < tmp.Length; ++i)
{
tmp[i] += rhs._NumberField[i];
}
return _Matrix(this->_Dimensional[0], this->_Dimensional[1], tmp);
}
///
/// 只有两个距陈是同型距陈时才可以进行加减法。
///
///
/// operator-(const _Matrix& rhs)
{
//(1)距陈的维度都是2
//(2)元素个数必须相同
//(3)必须是同型距陈(距陈A和B的行数和列数都相等)
assert(this->_Dimensional.Length == rhs._Dimensional.Length && this->_Dimensional.Length == 2);
assert(this->_Dimensional[0] == rhs._Dimensional[0] && this->_Dimensional[1] == rhs._Dimensional[1]);
assert(this->_NumberField.Length == rhs._NumberField.Length);
_Matrix ndvsResult;
_Array tmp = this->_NumberField;
for (int i = 0; i < tmp.Length; ++i)
{
tmp[i] -= rhs._NumberField[i];
}
return _Matrix(this->_Dimensional, tmp);
}
///
/// 定义5:
/// 设 k 为数域 p 中的数,向量(ka1,ka2...kan) 称为向量 a = (a1,a2,...an) 与数 k 的数量乘积,记为 ka
///
///
/// operator*(const int& k, const _Matrix& ndvs)
{
_Matrix ndvsResult;
_Array tmp = ndvs._NumberField;
for (int i = 0; i < tmp.Length; ++i)
{
tmp[i] *= k;
}
return _Matrix(ndvs._Dimensional, tmp);
}
///
/// 定义5:
/// 设 k 为数域 p 中的数,向量(ka1,ka2...kan) 称为向量 a = (a1,a2,...an) 与数 k 的数量乘积,记为 ka
///
///
/// operator*(const _Matrix& ndvs, const int& k)
{
return k * ndvs;
}
///
/// 矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时
/// 才有意义[1] 。一般单指矩阵乘积时,指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。
/// 由于它把许多数据紧凑地集中到了一起,所以有时候可以简便地表示一些复杂的模型,如电力系统网络模型。
///
/// 注意事项编辑 播报
/// 1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
/// 2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
/// 3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
///
///
///
/// operator*(const _Matrix& rLeft, const _Matrix& rRight)
{
if (rLeft.ColumnsCount != rRight.RowsCount)
{
_cout << _t("错误:矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(columns)和第二个矩阵的行数(rows)相同时才有意义。\n\n");
//当矩阵A的列数(columns)等于矩阵B的行数(rows)时,A与B可以相乘。
assert(rLeft.ColumnsCount == rRight.RowsCount);
}
//矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
_Matrix mResult(rLeft.RowsCount, rRight.ColumnsCount);
for (int i = 0; i < mResult.RowsCount; ++i)
{
//第 i + 1 行
for (int j = 0; j < mResult.ColumnsCount; ++j)
{
//(AB)ij = Ai1B1j + Ai2B2j +... + AipBpj
//p为A的列数,B的行数
T sum = 0;
for (int k = 0; k < rLeft.ColumnsCount; ++k)
{
sum = sum + rLeft.GetElement(i, k) * rRight.GetElement(k, j);
}
mResult.NumberField[i * mResult.ColumnsCount + j] = sum;
}
}
return mResult;
}
///
/// 返回某行的所有元素
///
/// 行索引
/// GetRows(int nRowIndex)const
{
assert(nRowIndex >= 0 && nRowIndex < RowsCount);
_Array arrResult(this->ColumnsCount);
for (int i = 0; i < ColumnsCount; ++i)
{
arrResult.Add(this->NumberField[nRowIndex * ColumnsCount + i]);
}
return arrResult;
}
///
/// 返回某列的所有元素
///
/// 列索引
/// GetColumns(int nColumnIndex)const
{
assert(nColumnIndex >= 0 && nColumnIndex < ColumnsCount);
_Array arrResult(this->RowsCount);
for (int i = 0; i < RowsCount; ++i)
{
arrResult.Add(this->NumberField[i * ColumnsCount + nColumnIndex]);
}
return arrResult;
}
///
/// 返回向量空间中坐标的元素引用
///
/// 坐标
///
/// 功能:判断是否对称矩陈
///
/// 对称矩陈定义:
/// 对称矩陈(symmetric matrix)是指其转置等于自己的矩陈,即满足 A == AT (T为转置)
/// 对称矩陈定义:
/// 在一个n阶方阵A中,若元素满足下述性质:Aij = Aji( i >= 0, j >=0; i <= n-1; j <= n-1),则称A为对称矩阵。
/// _cout << m1 + m2;
/// [1,0,-1]
/// A = [0,1,0] 是一个对称矩陈 1,0,-1,0,1,0,-1,0,1
/// [-1,0,1]
///
///
/// 判断矩陈是否对角矩陈。
/// 对象矩陈定义:
/// 对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2, ..., an) 。
/// 对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素
/// 相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、
/// 数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。
///
/// 主对角线定义:
/// 在一个n阶方阵(或是n阶行列式)中,从左上角到右下角这一斜线方向上的n 个元素所在的对
/// 角线,叫做n 阶方阵(或行列式)的主对角线。
///
/// coordinate = this->GetCoordinateFromIndex(i);
if (coordinate[0] != coordinate[1])
{
return false;
}
}
}
}
///
/// 判断矩陈是否单位矩陈。
/// 单位矩陈定义:
/// 单位矩陈(identity matrix)是一种特殊的对角矩陈,其主对角线元素为1,其余元素为0。
/// n阶单位矩陈 In 是一个n⨯n的方块矩陈,可以记为
/// In = diag(1, 1, ..., 1)
/// 一个 m ⨯ n 的矩陈A和单位矩陈的乘积等于其本身,即
/// AIn = Im A = A
///
/// coordinate = this->GetCoordinateFromIndex(i);
if (coordinate[0] != coordinate[1])
{
return false; //不是对角矩陈
}
if (n != 1) //不是单位矩陈
{
return false;
}
}
}
}
///
/// 获得与行数相等的单位矩陈
///
/// GetRowIdentityMatrix()const
{
_Matrix mResult(this->_Dimensional[0], this->_Dimensional[0]);
for (int i = 0; i < this->_Dimensional[0]; ++i)
{
mResult.SetValue(1, { i,i });
}
return mResult;
}
///
/// 获得与列数相等的单位矩陈
///
/// GetColumnIdentityMatrix()const
{
_Matrix mResult(this->_Dimensional[1], this->_Dimensional[1]);
for (int i = 0; i < this->_Dimensional[1]; ++i)
{
mResult.SetValue(1, { i,i });
}
return mResult;
}
///
/// 判断矩陈m是否这个矩陈的逆矩陈
/// 逆矩陈定义:
/// 对于一个n ⨯ n 的方块矩陈A,如果存在另一个方块矩陈B使得
/// AB = BA = In
/// 为单位矩陈,则称A是可逆的。矩陈B称为矩陈A的逆矩陈(inverse matrix),记为A - 1.
///
///
/// & m)const
{
//https://www.bilibili.com/read/cv2920478
//零矩阵是不可逆的(零矩阵,在数学中,特别是在线性代数中,零矩阵即所有元素皆为0的矩阵)
//定义: 单位矩阵的逆矩阵是它本身
if (this->ColumnsCount != m.RowsCount && this->RowsCount != m.ColumnsCount)
{
return false; //不能相乘
}
_Matrix A = *this * m;
_Matrix B = m * (*this);
_pcn(A);
_pcn(B);
if (A != B) return false;
if (A != GetRowIdentityMatrix() && A != GetColumnIdentityMatrix()) //A 不是单位矩陈
{
return false;
}
//这步不用,因为 A 和 B 是相等的
//if (B != GetRowIdentityMatrix() && B != GetColumnIdentityMatrix()) //B 不是单位矩陈
//{
// return false;
//}
return true;;
}
///
/// 求矩陈的 伴随矩陈
///
/// GetAdjugateMatrix()const
{
}
///
/// 求矩陈的 逆矩陈
///
/// GetInverseMatrix() const
{
_Matrix mResult;
//https://blog.csdn.net/u010551600/article/details/81504909 求解逆矩阵的常用三种方法
//1.待定系数法
_MatrixS ms1 = *this;
_MatrixS ms2(this->RowsCount, this->ColumnsCount);
_MatrixS ms3 = ms1 * ms2;
ms3.SetEquality(this->GetRowIdentityMatrix());
_Equation eq(ms3.NumberField);
_pcn(ms3);
_pcn(eq.Equality);
_pcn(eq.GetUnknowList());
//2.伴随矩阵求逆矩阵
//3.初等变换求逆矩阵
return mResult;
}
};
#ifdef _UNICODE_
template
std::wistream& operator >> (std::wistream& os, _Matrix& m)
{
_cout << _t("std::wistream& operator >> (std::wistream& os, _Array& m){未完成!\n");
return os;
}
template
std::wostream& operator<<(std::wostream& os, const _Matrix& m)
{
os << m.ToString();
return os;
}
#else
template
std::istream& operator >> (std::istream& os, _Matrix& m)
{
_cout << _t("std::wistream& operator >> (std::wistream& os, _Matrix& m){未完成!\n");
return os;
}
template
std::ostream& operator<<(std::ostream& os, const _Matrix& m)
{
os << m.ToString();
return os;
}
#endif
_LF_END_
#endif // !__LINEARALGEBRA_H_ _Matrix.cpp
#include "_Matrix.h"
_LF_BEGIN_
_MatrixS::_MatrixS(const _Matrix& intM)
{
_Dimensional = intM.Dimensional;
for (int i = 0; i < intM.NumberField.Length; ++i)
{
_NumberField[i] = _tostr(intM.NumberField[i]);
}
}
_MatrixS::_MatrixS()
{
}
///
/// 创建一个 m 行 n 列矩陈,如果不用变量表示,则对所有元素初化为 T(),
/// 如果用变量表示,则所有变量用 a~z A~Z 表示
///
///
///
/// 创建时间:2023-05-02 最后一次修改时间:2023-05-02
_MatrixS::_MatrixS(const int mRow, const int nColumn, bool bVariable)
{
assert(mRow >= 0 && nColumn >= 0);
this->_Dimensional = { mRow, nColumn };
if (!bVariable)
{
for (int i = 0; i < mRow * nColumn; ++i)
{
this->_NumberField.Add(_t("0"));
}
}
else
{
for (int i = 0; i < mRow * nColumn; ++i)
{
_string tmp;
_char c = 'a' + i;
tmp.Add(c);
this->_NumberField.Add(tmp);
}
}
}
_string _MatrixS::ToString() const
{
_string sResult;
int RowsCount = _Dimensional[0];
int ColumnsCount = _Dimensional[1];
sResult.Add(_t("\n"));
for (int i = 0; i < RowsCount; ++i)
{
int iLast = ColumnsCount - 1;
for (int j = 0; j < iLast; ++j)
{
sResult.Add(_NumberField[i * ColumnsCount + j]);
sResult.Add(_t(",\t\t"));
}
sResult.Add(_NumberField[i * ColumnsCount + iLast]);
sResult.Add(_t("\n"));
}
sResult.Add(_t("\n"));
return sResult;
}
_string& _MatrixS::GetElement(const int nRowIndex, const int nColumnsIndex) const
{
int n = nRowIndex * this->ColumnsCount + nColumnsIndex;
return this->_NumberField[n];
}
void _MatrixS::SetEquality(const _Matrix& intM)
{
for (int i = 0; i < intM.NumberField.Length; ++i)
{
_NumberField[i].Add(_t(" = "));
_NumberField[i].Add(_tostr(intM.NumberField[i]));
}
}
_MatrixS operator*(const _MatrixS& rLeft, const _MatrixS& rRight)
{
if (rLeft.ColumnsCount != rRight.RowsCount)
{
_cout << _t("错误:矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(columns)和第二个矩阵的行数(rows)相同时才有意义。\n\n");
//当矩阵A的列数(columns)等于矩阵B的行数(rows)时,A与B可以相乘。
assert(rLeft.ColumnsCount == rRight.RowsCount);
}
//矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
_MatrixS mResult(rLeft.RowsCount, rRight.ColumnsCount);
for (int i = 0; i < mResult.RowsCount; ++i)
{
//第 i + 1 行
for (int j = 0; j < mResult.ColumnsCount; ++j)
{
//(AB)ij = Ai1B1j + Ai2B2j +... + AipBpj
//p为A的列数,B的行数
_string sSum;
for (int k = 0; k < rLeft.ColumnsCount; ++k)
{
///sum = sum + rLeft.GetElement(i, k) * rRight.GetElement(k, j);
sSum.Add(rLeft.GetElement(i, k));
sSum.Add(_t(" * "));
sSum.Add(rRight.GetElement(k, j));
if (k != rLeft.ColumnsCount - 1)
{
sSum.Add(_t(" + "));
}
}
mResult.NumberField[i * mResult.ColumnsCount + j] = sSum;
}
}
return mResult;
}
_LF_END_ 变量类(初步)
/*******************************************************************************************
文件名 : _UnknownVar.h
作者 : 李锋
手机 : 13828778863
Email : [email protected]
功能 : 方程类,变量定义
创建时间 : 2023-05-04
最后一次修改时间 : 2023-05-04
方程(equation)是指含有未知数的等式。是表示两个数学式(如两个数、函数、量、运算)之间相等关
系的一种等式,使等式成立的未知数的值称为“解”或“根”。求方程的解的过程称为“解方程”。通过方程求解可以
免去逆向思考的不易,直接正向列出含有欲求解的量的等式即可。方程具有多种形式,如一元一次方程、二元一
次方程、一元二次方程等等,还可组成方程组求解多个未知数。在数学中,一个方程是一个包含一个或多个变量
的等式的语句。 求解等式包括确定变量的哪些值使得等式成立。 变量也称为未知数,并且满足相等性的未知数
的值称为等式的解。
********************************************************************************************/
#ifndef __UNKNOWNVAR_H_
#define __UNKNOWNVAR_H_
#include "X:\Work\Share\CCode\CPlatform\Base\global_c_all.h"
_LF_BEGIN_
///
/// 前置声明
///
class _Expression;
///
/// 未知数,变量
///
class _UnknownVar : public _Object
{
public:
///
/// 变量名子
///
_string Name;
///
/// 空为未赋值
///
_string Value;
public:
_UnknownVar(const _string sName);
inline _UnknownVar() {};
//乘法运算符重载
friend _Expression operator*(const _UnknownVar& lVar, const _UnknownVar& rVar);
//负号运算符重载
_Expression operator -();
_UnknownVar& operator=(const int iValue);
///
/// 重载减号
///
///
///
///
/// "^"符号在数学中通常表示乘方运算,即一个数的自乘。例如,2的3次方可以表示为2^3=8。
/// 8 的开方为 = 8 ^ 1/2
/// 8 的2次方为 = 8 ^ 2
/// 8 的开3次方为 = 8 ^ 1/3
/// 8 的3次方为 = 8 ^ 3
/// 8 的-3次为 = 8 ^ -3 = 1 / 8^3 (8的三次方的倒数) 倒数:设x为正整数,则x的倒数为1/x。
///
/// 变量
/// 2表示平方,1/2 表示开2次方,-2表示平方的倒数,以次类推......
/// #include "_UnknownVar.h"
#include "_Expression.h"
_LF_BEGIN_
_Expression operator*(const _UnknownVar& l, const _UnknownVar& r)
{
return _Expression(l.Name + _t("*") + r.Name, { l });
}
///
/// 重载减号
///
///
///
///
/// 负号运算符重载
///
/// 表达式类(初步)
/*******************************************************************************************
文件名 : _Expression.h
作者 : 李锋
手机 : 13828778863
Email : [email protected]
功能 : 表达式
创建时间 : 2023-05-06
最后一次修改时间 : 2023-05-06
********************************************************************************************/
#ifndef __EXPRESSION_H_
#define __EXPRESSION_H_
#include"_UnknownVar.h"
_LF_BEGIN_
///
/// 数学表达式
///
/// 创建时间:2023-05-06 最后一次修改时间:2023-05-06
class _Expression : public _Object
{
private:
///
/// 变量列表
///
_DList<_UnknownVar> _VarList;
_string _sExpression;
public:
_Expression(const _string& sExpression);
_Expression(const _string& sExpression, const _DList<_UnknownVar> &VarList);
virtual _string ToString() const override;
};
_LF_END_
#endif //-------------------------------------------------------------------__EXPRESSION_H_#include "_Expression.h"
_LF_BEGIN_
_Expression::_Expression(const _string& sExpression)
{
_sExpression = sExpression;
}
_Expression::_Expression(const _string& sExpression, const _DList<_UnknownVar>& VarList)
{
_sExpression = sExpression;
_VarList = VarList;
}
_string _Expression::ToString() const
{
return _sExpression;
}
_LF_END_方程类:(初步)
/*******************************************************************************************
文件名 : _Equation.h
作者 : 李锋
功能 : 方程类
创建时间 : 2023-05-02
最后一次修改时间 : 2023-05-02
方程(equation)是指含有未知数的等式。是表示两个数学式(如两个数、函数、量、运算)之间相等关
系的一种等式,使等式成立的未知数的值称为“解”或“根”。求方程的解的过程称为“解方程”。通过方程求解可以
免去逆向思考的不易,直接正向列出含有欲求解的量的等式即可。方程具有多种形式,如一元一次方程、二元一
次方程、一元二次方程等等,还可组成方程组求解多个未知数。在数学中,一个方程是一个包含一个或多个变量
的等式的语句。 求解等式包括确定变量的哪些值使得等式成立。 变量也称为未知数,并且满足相等性的未知数
的值称为等式的解。
********************************************************************************************/
#ifndef __EQUATION_
#define __EQUATION_
#include "_UnknownVar.h"
_LF_BEGIN_
class _Equation : public _Object
{
private:
///
/// 等式,或者代码
///
_StringList _Equality;
///
/// _Pair1 是未知数,_Pair2 是含有未知数的等式
///
_DList < _Pair<_string, _StringList> > _UnknownList;
public:
///
/// 等式列表
///
__declspec(property(get = GetEquality)) const _StringList& Equality;
///
/// 获取等式列表
///
inline const _StringList& GetEquality() const { return _Equality; }
public:
///
///
///
/// 方程等式
/// 创建时间:2023-05-02 最后一次修改时间:2023-05-02 (已测试)
_Equation(const _StringList& slEquality);
_Equation(const _Array<_string>& arrEquality);
_StringList GetUnknowList()const;
};
_LF_END_
#endif //----------------------------------------------------------- __EQUATION_
#include "_Equation.h"
_LF_BEGIN_
_Equation::_Equation(const _StringList& slEquality)
{
//优化等式
//1 * a + 2 * c = 1, 1 * b + 2 * d = 0
// - 1 * a + -3 * c = 0, -1 * b + -3 * d = 1
for (_string s : slEquality)
{
}
_Equality = slEquality;
}
_Equation::_Equation(const _Array<_string>& arrEquality)
{
const _char* sCaption = _t("_Equation::_Equation(const _Array<_string>& arrEquality)");
//优化等式
//1 * a + 2 * c = 1, 1 * b + 2 * d = 0
// - 1 * a + -3 * c = 0, -1 * b + -3 * d = 1
// (-1 * a ) * (a + c ) = 2 * d
// a**5 => a 五次方
// 256 ** (1/4) == 4
// 4 ** 4 == 256
for (_string s : arrEquality)
{
//第一步,去掉空格
_char* ps = (_char*) s.Data;
_string tmp = s.RemoveChar(_t(' '));
_string sResult(_t(""), tmp.Length);
//第二步,分解等式
//_StringList sl(s.std_c_str(), _t("="));
//if (sl.Count != 2)
//{
// d.ShowError(_t("等式错误!"), sCaption);
//}
//第三步,优化等式
ps = (_char*)tmp.Data;
for (int i = 0; i < tmp.Length; ++i)
{
if (ps[i] == _t('*'))
{
int j = i - 1;
if (j < 0)
{
d.ShowError(_t("等式错误,*号前面没有字符!"), sCaption);
break;
}
_string word1,word2;
for ( ; j >= 0; --j)
{
if (ps[j] == _t('/') || ps[j] == '*' || ps[j] == '-' || ps[j] == _t('+'))
{
break;
}
else
{
word1.Add(ps[j]);
}
}
if (word1 == _t("1"))
{
ps[j+1] = _t(' ');
}
_pcn(word1.Reversal());
j = i + 1;
if (j > tmp.Length - 1)
{
d.ShowError(_t("等式错误,*号后面没有字符!"), sCaption);
break;
}
for (; j < tmp.Length; ++j)
{
if (ps[j] == _t('/') || ps[j] == '*' || ps[j] == '-' || ps[j] == _t('+'))
{
if (word2 == _t("1"))
{
ps[j - 1] = _t(' ');
}
break;
}
word2.Add(ps[j]);
}
_pcn(word2);
ps[i] = _t(' ');
}
}
tmp = tmp.RemoveChar(_t(' '));
ps = (_char*)tmp.Data;
//第三步,去括号
if (s.IndexOf(_t("(")) != -1)
{
}
_Equality.Add(tmp);
}
}
///
/// 返回未知数列表
///
///