搜索算法（五） DFS BFS 练习题

练习题

1.
力扣https://leetcode.cn/problems/surrounded-regions/这题和417类似，都是从边界朝内部搜索，417用的是DFS，这里为了练习，就用BFS。

首先从四条边界得到‘O’的坐标，加入队列。接着一层一层搜索，将所有相邻且为‘O'元素坐标加入队列，并且标记为已访问。

搜索结束后，遍历整个数组，将所有未访问的'O'标记为'X'，因为所有边界可达的'O'都已被标记为访问过。

class Solution {
public:
    void solve(vector>& board) {
        int m = board.size();
        int n = board[0].size();
        queue> q;
        vector> visit(m,vector(n,false));
        for(int i=0;i path = {-1,0,1,0,-1};
        while(!q.empty()){
            int k = q.size();
          
            for(int i=0;i=0 && x=0 && y

2.力扣https://leetcode.cn/problems/binary-tree-paths/这题是一道典型的DFS，题目不难，但注意不要写成引用传递了。

不然就会像我一开始那样，string插入弹出写了半天，老是不对。（因为确定不了一个数字到底是几位char）

仔细一看，写成值传递，这样函数结束时，path上新增的内容都会自然消除。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector binaryTreePaths(TreeNode* root) {
        vector res;
        dfs(root,"",res);
        return res;
    }

    void dfs(TreeNode* root, string path, vector& res){
       if(root){
           path += to_string(root->val);
           if(!root->left && !root->right){
               res.push_back(path);
           }else{
               path += "->";
               dfs(root->left,path,res);
               dfs(root->right,path,res);
               
           }
       }
    }


};

3.力扣https://leetcode.cn/problems/permutations-ii/

这题是典型的DFS，考虑到重复数字直接DFS，会产生重复的排列，有两种解决方法。

一是用set存储排列，自动去除了重复的排列。

二是跳过与前一个数字重复的数字（且前一个数字是未访问的）。

这里采用第二种方法：

class Solution {
public:
    vector> permuteUnique(vector& nums) {
        int n = nums.size();
        vector path;
        vector> res;
        vector visit(n,false);
        sort(nums.begin(), nums.end());
        
        dfs(nums,path,res,visit);
            
        return res;
    }

    void dfs(vector& nums, vector path, vector>& res, vector visit){
        if(path.size()==nums.size()){
            res.push_back(path);
        }else{
            int n = nums.size();
            for(int i=0;i

4.力扣https://leetcode.cn/problems/sudoku-solver/

解数独的关键在于记录每行每列每个3x3方块的数字，然后对空格处依次遍历可能的数字。

先预处理矩阵，然后DFS，需要注意的是DFS的递归方法中，最后找到目标解法后，要在每一层递归直接return，不然会继续遍历可能的数字。

class Solution {
public:
    void solveSudoku(vector>& board) {
        memset(row,false,sizeof(row));
        memset(col,false,sizeof(col));
        memset(cube,false,sizeof(cube));


        for(int i=0;i<9;i++){
            for(int j=0;j<9;j++){
                if(board[i][j]=='.'){
                    path.push_back({i,j});
                }else{
                    int m = board[i][j] - '0';
                    row[i][m] = col[j][m] = cube[i/3][j/3][m] = true;
                }
            }
        }

        dfs(board,0);
    }

    bool dfs(vector>& board, int x){
        if(x>=path.size()){
            return true;
        }
        auto [a,b] = path[x];
        for(int i=1;i<=9;i++){
            if(!row[a][i] && !col[b][i] && !cube[a/3][b/3][i]){
                row[a][i] = col[b][i] = cube[a/3][b/3][i] = true;
                board[a][b] = '0' + i;
                if(dfs(board,x+1))
                    return true;
                row[a][i] = col[b][i] = cube[a/3][b/3][i] = false;
            }
        }
        return false;
    }

private:
    bool row[9][10];
    bool col[9][10];
    bool cube[3][3][10];
    vector> path;
};

5.力扣https://leetcode.cn/problems/minimum-height-trees/这题挺绕的，记忆化DFS过不了所有的答案，必须要用拓朴排序。

虽然我不懂 这种解法为啥要叫拓扑排序，但看题解都这么说那就是了吧。

拓朴排序解这道题就绕开了搜索的问题。

要找高度最小的根节点，这个根节点应该出现在两个相距最远的叶子节点的中间位置。不然的话，其中一个子树的高度就会很高。

举个例子，两个叶子节点相距11，如果我选最中间的节点作为根节点，那么树高度为6.

如果随便选了叶子节点相邻的节点作为根节点，那么树高度为9。

有了这个思想之后，怎么实现代码呢？

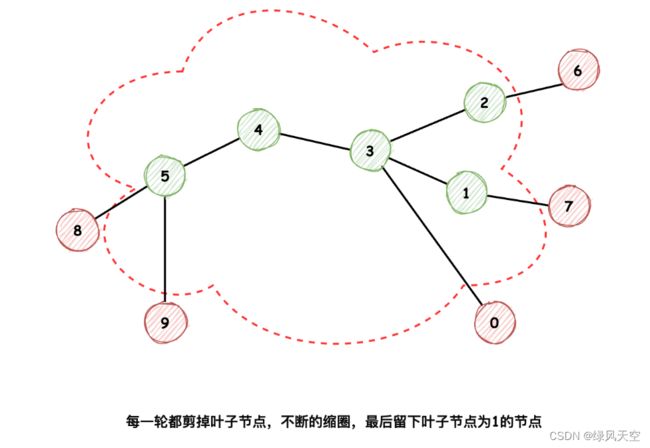
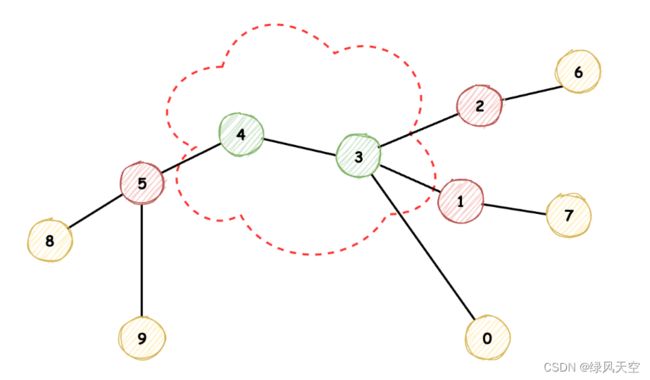
这个题解链接里的这两张图很好地说明了方法：

 

目标是寻找距离最远的两个叶子节点的中间节点，我们无法立刻知道哪两个叶子节点相距最远。

所以每次都删除掉最外围的叶子节点（也就是入度为1的节点），删掉叶子节点之后，与它们相连的入度为2的节点就会变成新的叶子节点，这样新一轮继续删除叶子节点，更新与它们相连的节点的度数。

这里有些类似层次遍历，每一次删除最外层节点，当删除到只剩下两个或一个节点时，可以认为它们是最中间的节点，作为答案返回。 

看上图还是挺生动形象的，从相距最远的节点，一层一层剥开，最后找到中心节点。

代码：

class Solution {
public:
    vector findMinHeightTrees(int n, vector>& edges) {
       if(n==1) return vector{0};
       vector degree(n,0);
       vector> connect(n);
       for(auto e:edges){
        connect[e[0]].emplace_back(e[1]);
        connect[e[1]].emplace_back(e[0]);
        degree[e[0]]++;
        degree[e[1]]++;
       }
        
       queue q;
       for(int i=0;i2){
           int m = q.size();
           n -= m;
          
           for(int i=0;i res;
       while(q.size()>0){
           res.push_back(q.front());
           q.pop();
       }
       return res;


    }




   
};

Reference:

力扣