GIS tips：基于弗雷歇（Frechet）距离的曲线/形状相似度计算方法（python）

---

前言

最近在研究线的相似度匹配，自然而然地了解到两个比较好的相似度匹配方法，分别是弗雷歇距离和隐式马尔科夫模型。本文主要介绍如何通过python实现不同曲线/形状之间基于弗雷歇距离的相似度计算。

知乎链接：GIS tips：基于弗雷歇（Frechet）距离的曲线/形状相似度计算方法（python）

1.弗雷歇距离简介

利用弗雷歇距离来实现线的相似度匹配，其相关已经有很多文章介绍过了，在此给出一些作者看过介绍的比较全面的博客，以供大家参考：
离散Fréchet（弗雷歇） 距离评价曲线相似度

本文主要集中在其算法实现，因此，大家只用记住一点就可以了：弗雷歇距离可以服务于线相似度匹配。
相关的文献也有很多，在此不再一一列举。

2.用python实现它的原因

我发现弗雷歇距离在Postgis里面已经有成熟的实现方案了，可惜调用比较麻烦，这个库不是python的，链接如下：
http://postgis.net/docs/ST_FrechetDistance.html
作者尝试了python支持的其他几个常用GIS库，诸如shapely、geopy等等，但都没有发现现成的接口，如果有知道的小伙伴可以在评论区或私信指点我一下QAQ。
听师兄说python也可以使用Postgis上的接口，但因为在配置环境、安装各种库的过程中遇到了许多挫折和困难，最终决定自己用python实现一下，供大家批评指正。

---

一、节点数相同的曲线/形状弗雷歇距离计算

1.引用库

弗雷歇距离相似度计算：
https://github.com/nelsonwenner/shape-similarity
该库安装方法十分简单，直接使用pip即可：

pip install shapesimilarity

该库结合了Frechet距离和Procrustes分析来检查两个形状/曲线之间的相似性。在实现过程中，首先使用Procrustes分析对曲线进行归一化，然后计算曲线之间的Fréchet距离。
注意事项：
该库的输入必须是节点数相等的！！！

2.代码示例

应用该库的代码示例如下，输入的形状/曲线可以用下述两种方法生成，详细使用方式请参照详细注释：

from shapesimilarity import shape_similarity
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(1, -1, num=200)

# 方法一 通过函数构建曲线
y1 = 2*x**2 + 1
y2 = 2*x**3 + 2
shape1 = np.column_stack((x, y1))
shape2 = np.column_stack((x, y2))

# 方法二 直接输入节点坐标(x, y)
shape3 = [(1.4, 2.6),(1.5, 5.6),(5.8, 10),(10.6, 9)]
shape4 = [(1.5, 2.7),(1.9, 5.4),(5.7, 12),(14.6, 5)]
shape3 = np.column_stack(shape3)
shape4 = np.column_stack(shape4)

# 调用库计算相似度
similarity1 = shape_similarity(shape1, shape2)
similarity2 = shape_similarity(shape3, shape4)

# 方法一和方法二的相似度输出
print("similarity1:{}".format(similarity1))
print("similarity2:{}".format(similarity2))

# 图形展示部分
# 方法一：
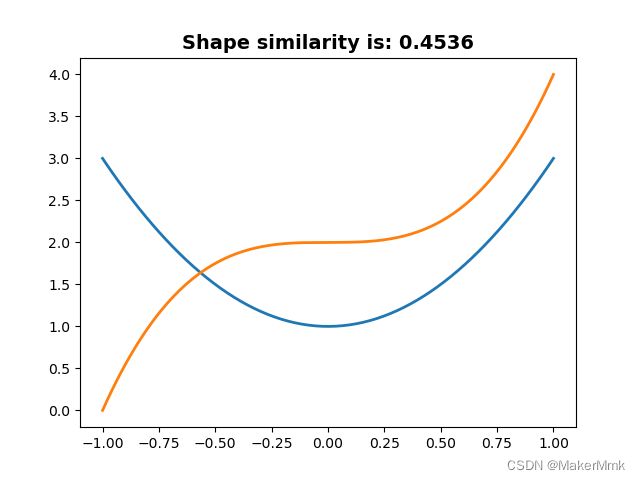
plt.plot(shape1[:, 0], shape1[:, 1], linewidth=2.0)
plt.plot(shape2[:, 0], shape2[:, 1], linewidth=2.0)

plt.title(f'Shape similarity is: {similarity1}', fontsize=14, fontweight='bold')
plt.show()

# 方法二
plt.plot(shape3[:, 0], shape3[:, 1], linewidth=2.0)
plt.plot(shape4[:, 0], shape4[:, 1], linewidth=2.0)

plt.title(f'Shape similarity is: {similarity2}', fontsize=14, fontweight='bold')
plt.show()

3.结果展示

输出结果：

similarity1:0.4536
similarity2:0.9017

输出图像（仅展示方法1的输出）：

二、节点数不同的曲线/形状基于弗雷歇的相似度计算

虽然我找到上面那个库的结果很哇塞，但是很快就发现了一个致命问题：
实际使用过程中大多数线要素和形状都是不等节点的！
突然感觉世界灰暗了，随即硬着头皮想出了解决方案并实现。实现的总体思路如下：

1.读取输入数据(数据预处理请自行添加)；——对应test.py
2.根据线的节点坐标，根据阈值重新构建节点，保证重新构建后节点数一致；
——对应frechet.py
3.调用shapesimilarity库进行计算并成果展示。——对应frechet.py中的similarity函数

1.代码介绍

与前文相同，该部分代码依旧引用了该库：

pip install shapesimilarity

首先我将输入部分和运算部分进行了划分，方便后续代码改造（输入部分在test.py和frechet_distance_curve.py），然后结合shpesimilarity库完成了节点数不同的曲线/形状基于弗雷歇距离的相似度计算（frechet.py），line.py是代码设计的类，我单独放置在一个文件之中。
不同节点相似度匹配的核心思想是将不等节点变更更为等节点，即根据两条曲线的节点和长度重新构建新的节点，并将其匹配，因本文仅研究曲线/形状形态的相似度，故不用过多考虑空间关系。
将下面的代码逐一复制，根据标题名命名.py文件，如图将其放在同一根目录下，从test.py运行即可（test.py读取数据请自行改造）：

2.test.py

import frechet_distance_curve

if __name__ == "__main__":
    c1 = [(0.45, 1.6),  (4.9, 1.5), (3.9, 1.5)]
    c2 = [(0.45, 1.6), (2.7, 1.6), (2.7, 1.1), (3.7, 1.6)]
    if len(c1) != 0 and len(c2) != 0:
    	frechet_distance_curve.test_2d_curve(c1, c2)
    else:
        print("error: can not input empty!")

3.frechet_distance_curve.py

import line
import frechet
def test_2d_curve(c1, c2):
    # 建立CurveByLines类，a，b具有一定的属性、方法了
    # 具体包含：线集，差集，at方法
    a = line.CurveByLines(c1)
    b = line.CurveByLines(c2)
    # 标准化格式后的线，进行弗雷歇距离计算，a，b是一个可迭代的对象
    frechet.frechet_distance(a, b)

4.frechet.py

from typing import Any, Callable, List
from shapesimilarity import shape_similarity
import numpy as np
import matplotlib.pyplot as plt
import line

# 弗雷歇距离求和
def transform(l):
    return [list(el) for el in l]

def similarity(l1, l2):

    r1 = transform(l1)
    print("r1:{}".format(r1))
    r2 = transform(l2)

    shape1 = np.row_stack(r1)
    shape2 = np.row_stack(r2)

    print("shape1:{}".format(shape1))

    similarity = shape_similarity(shape1, shape2)

    print("similartiy:{}".format(similarity))

    # print(similarity)

    plt.plot(shape1[:, 0], shape1[:, 1], linewidth=2.0)
    plt.plot(shape2[:, 0], shape2[:, 1], linewidth=2.0)

    plt.title(f'Shape similarity is: {similarity}', fontsize=14, fontweight='bold')
    plt.show()


def frechet_distance(
    # ->常常出现在python函数定义的函数名后面，为函数添加元数据,描述函数的返回类型，也可以理解为给函数添加注解
    # 形参后面加冒号其实是添加注释，告诉使用者每个形参、返回值的类型，这里只是建议，传入其他类型也并不会报错
    # 此处若传入的为曲线，则接受的为CurveByLines类
    l1: line.Line,
    l2: line.Line,
    # 节点数，离散化阈值
    n_disc_l1: int = 100,
    n_disc_l2: int = 100,
    # 星号将多个实参合并为一个元组
    *,
    # 预设的阈值
    prec: float = 0.001,

) -> float:
    print(l1)
    # 输入中，l1、l2为曲线，n_xx为分段数
    distance_matrix(l1, l2, n_disc_l1, n_disc_l2)

# 离散化，求距离矩阵（二维数组） 距离矩阵
def distance_matrix(l1:line.Line, l2:line.Line, nd1:int, nd2:int) -> List[List[float]]:

    # 此时的l1于l2依旧是curve类
    # 保留曲线的起点，在后面将其细分为参数份
    ld1 = list(line.discretize(l1, nd1))
    print(ld1)
    ld2 = list(line.discretize(l2, nd2))
    similarity(ld1, ld2)

5.line.py

# collections模块还提供了几个额外的数据类型：Counter、deque、defaultdict、namedtuple和OrderedDict等。
# 1.namedtuple: 生成可以使用名字来访问元素内容的tuple
# 2.deque: 双端队列，可以快速的从另外一侧追加和推出对象
# 3.OrderedDict: 有序字典
# 4.defaultdict: 带有默认值的字典
# 5.Counter: 计数器，主要用来计数

from typing import Tuple, Iterable, Callable, Collection, List
# 要定义一个类型别名，可以将一个类型赋给别名。类型别名可用于简化复杂类型签名，在下面示例中，Vector 和 list[float] 将被视为可互换的同义词：
# Vector = list[float]
Point = Collection[float]

class Line:
    # 将形参给到pbeg和pend，同时检查他们是否是Point类类型，相当于强制类型检查
    def __init__(self, pbeg:Point, pend:Point):
        self.pbeg = pbeg
        self.pend = pend
        # zip() 函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表。
        # zip([iterable, ...])
        # >>> a = [1,2,3]
        # >>> b = [4,5,6]
        # >>> c = [4,5,6,7,8]
        # >>> zipped = zip(a,b)     # 打包为元组的列表
        # [(1, 4), (2, 5), (3, 6)]
        # >>> zip(a,c)              # 元素个数与最短的列表一致
        # [(1, 4), (2, 5), (3, 6)]
        # 这样的话就仅照顾距离最短的线，并求出了差集
        self.pdlt = [(ev - bv) for bv, ev in zip(self.pbeg, self.pend)]


    def at(self, x:float) -> Point:
        # lt是差集，用x乘以差集再加上第一条直线
        return tuple(bv + x * dv for bv, dv in zip(self.pbeg, self.pdlt))


# 由线建立曲线的类
class CurveByLines(Line):
    def __init__(self, pts: Collection[Point]):
        # 自身属性
        self.lines = [Line(pbeg, pend) for pbeg, pend in zip(pts, pts[1:])]

    # 此处对Curve类进行分步处理，x为一个比例，处在[0，1]区间
    def at(self, x: float) -> Point:
        # 首先按比例找到对应的lines索引
        x_with_lines = x * len(self.lines)
        # 找到离索引最近的实际坐标点索引值，且不能超出最大索引范围
        li = min(int(x_with_lines), len(self.lines) - 1)
        print(self.lines[li].at(x_with_lines - li))
        # 此处返回的其实就是分好段的离散坐标了
        return self.lines[li].at(x_with_lines - li)

class CurveByFormula(Line):
    def __init__(self, f: Callable[[float], Point]):
        self.f = f

    def at(self, x:float) -> Point:
        return self.f(x)

def discretize(line:Line, n:int, xbeg:float=0.0, xend:float=1.0) -> Iterable[Point]:
    # 此处的line为curve，是一个line的集合
    xinv = xend - xbeg
    # 即：此处的at应参考curve类中的at方法
    return (line.at((i / n) * xinv + xbeg) for i in range(0, n+1))

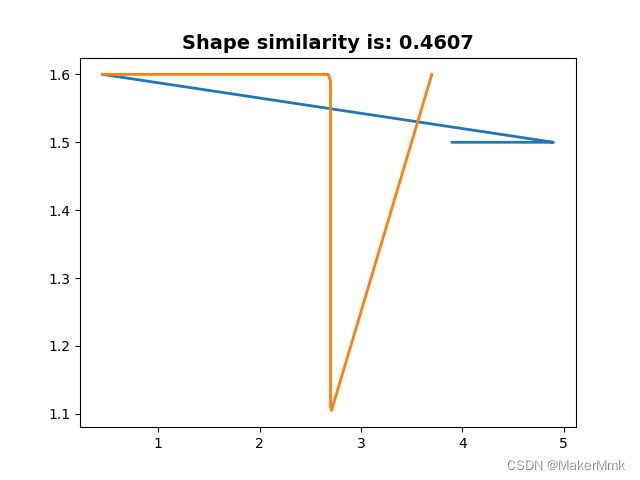
6.结果展示

---

总结

以后会时长更新在GIS学习中和论文产出过程中的一些小tips，内容包括但不限于GIS方法、深度学习和图像处理相关的知识方法，大家可以在评论区一起交流进步，请多多关注，谢谢。