【数据结构】二叉树链式结构的实现

1、前置说明

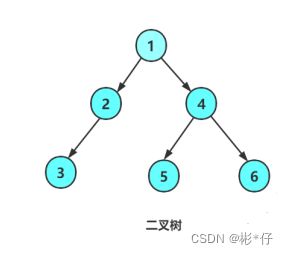
我们在前面的文章《数的概念与堆的实现》中讲到了特殊二叉树——堆的顺序存储，这篇文章我们来讲数的链式存储。普通的二叉树不能进行增删查改（搜索二叉树可以进行增删查改），也就不能通过增删查改的方式去构建一颗二叉树，因此为了了解二叉树的链式结构，我们先手动暴力创建一颗树。

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//暴力创建一棵树
BTNode* CreateTree()
{
	BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));
	assert(n1);

	BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));
	assert(n2);

	BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));
	assert(n3); 
	
	BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));
	assert(n4);

	BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));
	assert(n5);

	BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));
	assert(n6);

	n1->data = 1;
	n2->data = 2;
	n3->data = 3;
	n4->data = 4;
	n5->data = 5;
	n6->data = 6;

	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n2->right = NULL;
	n4->left = n5;
	n4->right = n6;
	n3->left = NULL;
	n3->right = NULL;
	n5->left = NULL;
	n5->right = NULL;
	n6->left = NULL;
	n6->right = NULL;

	return n1;

}

int main()
{
	BTNode* root = CreateTree();
	
	return 0;
}

1、上述手动创建的二叉树形式为：

2、二叉树的遍历

2.1 二叉树的前序遍历

二叉树的前序遍历又叫先根遍历，即以（根左右）的顺序来访问二叉树，例如上述二叉树的的前序遍历应该为
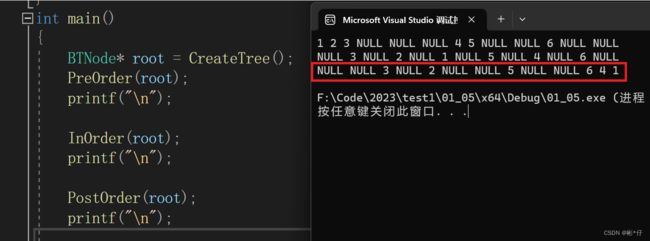
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL，子节点为空的时候用NULL来代替。

每个节点都符合（根左右）的顺序。

前序遍历代码实现：

//二叉树前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data); //打印当前节点的值
	PreOrder(root->left);
	PreOrder(root->right);
}

采用递归的思路，当遇到叶子节点为空的时候，直接返回（返回是返回调用的上一层函数），如果没有遇到空的叶子节点，继续调用前序遍历函数去找左树，左树找完了返回，再调用前序遍历函数去找右树。

在主函数中调用前序遍历函数

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	
	return 0;
}

调用结果

因为我们在遇到空返回之前，将代指空的NULL也打印了，所以打印结果如我们前述一致。

2.2 二叉树的中序遍历

二叉树的中序遍历又叫中根遍历，即以（左根右）的顺序来访问二叉树，例如上述二叉树的的中序遍历应该为（NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL），子节点为空的时候用NULL来代替

每个节点都符合（左根右）的顺序。

中序遍历代码实现：

//二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return 0;
	}

	InOrder(root->left);
	printf("%d ", root->data); //打印当前节点的值
	InOrder(root->right);
}

采用递归的思路，当遇到叶子节点为空的时候，直接返回（返回是返回调用的上一层函数），如果没有遇到空的叶子节点，继续调用中序遍历函数去找左树，左树找完了返回，先打印当前节点的值，当前节点对应前面的左树和后面要找的右树，相当于根节点，然后再调用中序遍历函数去找右树。

在主函数中调用中序遍历函数

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	
	return 0;
}

调用结果

因为我们在遇到空返回之前，将代指空的NULL也打印了，所以打印结果如我们前述一致。

2.3 二叉树的后序遍历

二叉树的后序遍历又叫后根遍历，即以（左右根）的顺序来访问二叉树，例如上述二叉树的的后跟遍历应该为（NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1），子节点为空的时候用NULL来代替

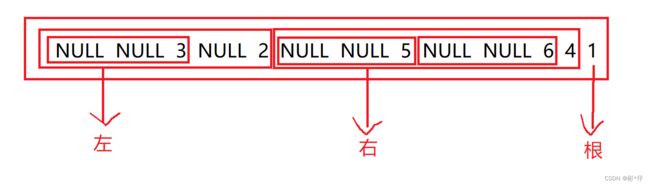
每个节点都符合（左右根）的顺序。

后序遍历代码实现：

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return 0;
	}
	
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);//打印当前节点的值
}

采用递归的思路，当遇到叶子节点为空的时候，直接返回（返回是返回调用的上一层函数），如果没有遇到空的叶子节点，继续调用后序遍历函数去找左树，左树找完了返回，再调用后序遍历函数去找右树，最后打印当前节点的值，此时这里节点相对前面的左树与右树，是他们的根节点。

在主函数中调用后序遍历

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	
	return 0;
}

打印结果

因为我们在遇到空返回之前，将代指空的NULL也打印了，所以打印结果如我们前述一致。

3、计算二叉树节点个数

思路：利用递归的思想，二叉树中节点的总个数=根节点（1）+左数的节点个数+右树的节点个数

计算二叉树节点个数代码实现：

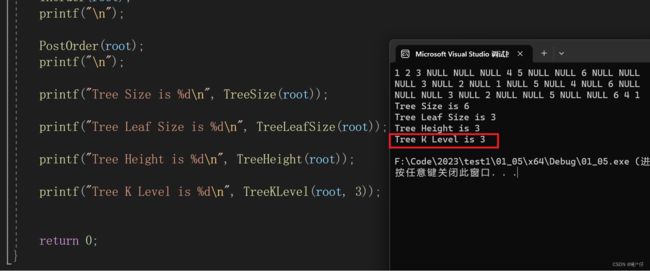
//计算二叉树节点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left)
		+ TreeSize(root->right) + 1;
}

1、如果节点为空，说明以此节点为根节点的树中没有节点，返回0。
2、如果根节点不为空，二叉树中节点的总个数=根节点（1）+左数的节点个数+右树的节点个数

在主函数中调用

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	printf("Tree Size is %d\n", TreeSize(root));
	
	return 0;
}

打印结果

1、经过计算之前手动创建的数一共有（1、2、3、4、5、6）6个节点。

4、计算叶子节点的个数

思路：利用递归的思想，一颗二叉树中叶子节点的个数=左树叶子节点的个数+右树叶子节点的个数

计算叶子节点的个数代码实现：

//计算叶子节点的个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right); 
}

1、如果节点为空，说明以此节点为根节点的树中没有节点，即也没有叶子节点，返回0。
2、节点不为空时，如果此节点的左子节点与右子节点同时为空，说明此节点是整颗树中的叶子节点，计数为1个叶子节点，返回1（返回到上一层调用他的函数中）。
3、前面两个条件语句都还不符合时，去找左子树的叶子节点与右子树的叶子节点，不断递归，左子树的叶子节点与右子树的叶子节点相加，即是整颗树的叶子节点。

在主函数中调用

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	printf("Tree Size is %d\n", TreeSize(root));

	printf("Tree Leaf Size is %d\n", TreeLeafSize(root));

	
	return 0;
}

打印结果

1、经过计算，之前手动创建的树中，一共有（3、5、6）3个叶子节点。

5、计算树的高度

思路：利用递归的思想，整颗树的高度等于左子树的高度或者右子树的高度两者中较大的一方加一。

计算树的高度代码实现：

//计算树的高度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int lh = TreeHeight(root->left);
	int rh = TreeHeight(root->right);
	return lh > rh ? lh + 1 : rh + 1;
}

在主函数中调用

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	printf("Tree Size is %d\n", TreeSize(root));

	printf("Tree Leaf Size is %d\n", TreeLeafSize(root));

	printf("Tree Height is %d\n", TreeHeight(root));

	
	return 0;
}

打印结果

1、经过计算，之前手动创建的树中，树的高度为3。

6、计算第K层节点个数

思路：利用递归思想，计算第K层节点的个数=计算子树第K-1层节点的个数

计算第K层节点个数代码实现：

//第K层节点个数
int TreeKLevel(BTNode* root, int k)
{
	assert(k > 0);
	
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	//转换成子树的第K-1层
	return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

1、首先要保证k大于0，所以要用是assert断言。
2、当节点为空时，说明此处无节点，返回0。
3、当不断迭代，k=1时，说明已经来到了第k层，将此节点计数为1，返回上一层调用他的函数。
4、第k层的节点总数等与左子树与右子树的第k-1层节点数相加，即第子树的k-1层节点总数。

在主函数中调用

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	printf("Tree Size is %d\n", TreeSize(root));

	printf("Tree Leaf Size is %d\n", TreeLeafSize(root));

	printf("Tree Height is %d\n", TreeHeight(root));

	printf("Tree K Level is %d\n", TreeKLevel(root, 3));

	
	return 0;
}

打印结果

1、之前手动创建的树的第三层一共有三个节点。

7、返回x所在的节点

思路：利用迭代思想，x所在的位置要不就在根节点，要不就存在与左子树或者右子树上，即去左子树或者右子树找。

返回x所在的节点代码实现：

//返回x所在的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)
	{
		return root;
	}

	//先去左树找
	BTNode* lret = TreeFind(root->left, x);
	if (lret)
	{
		return lret;
	}

	//左树没有找到，再到右树找
	BTNode* rret = TreeFind(root->right, x);
	if (rret)
	{
		return rret;
	}

	//左树、右树都没有找到
	return NULL;
}

1、当节点为空时，肯定不是要找的节点，向上一层函数返回一个空NULL。
2、当节点不为空时，查看其中的数值是否为要找的值，是的话向上一层函数返回此节点的数值。
3、如果都不是，继续去左子树和右子树上找。

在主函数中调用

int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	printf("Tree Size is %d\n", TreeSize(root));

	printf("Tree Leaf Size is %d\n", TreeLeafSize(root));

	printf("Tree Height is %d\n", TreeHeight(root));


	printf("Tree K Level is %d\n", TreeKLevel(root, 3));

	printf("Tree Find %p\n", TreeFind(root, 4));

	
	return 0;
}

打印结果

1、如打印结果所示，4在树中被找到了，且地址被返回了。

8、销毁一棵树

思路：根据迭代思想，只要将左子树销毁了，右子树销毁了，再将根节点释放了，这棵树也就被销毁了

代码实现：

void BinaryTreeDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}

9、完整代码

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//二叉树前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data); //打印当前节点的值
	PreOrder(root->left);
	PreOrder(root->right);
}

//二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return 0;
	}

	InOrder(root->left);
	printf("%d ", root->data); //打印当前节点的值
	InOrder(root->right);
}

//二叉树后续遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return 0;
	}
	
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);//打印当前节点的值
}

//计算二叉树节点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left)
		+ TreeSize(root->right) + 1;
}

//计算叶子节点的个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right); 
}

//计算树的高度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int lh = TreeHeight(root->left);
	int rh = TreeHeight(root->right);
	return lh > rh ? lh + 1 : rh + 1;
}

//第K层节点个数
int TreeKLevel(BTNode* root, int k)
{
	assert(k > 0);
	
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	//转换成子树的第K-1层
	return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

//返回x所在的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)
	{
		return root;
	}

	//先去左树找
	BTNode* lret = TreeFind(root->left, x);
	if (lret)
	{
		return lret;
	}

	//左树没有找到，再到右树找
	BTNode* rret = TreeFind(root->right, x);
	if (rret)
	{
		return rret;
	}

	//左树、右树都没有找到
	return NULL;
}

//销毁一棵树
void BinaryTreeDestroy(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}

//暴力创建一棵树
BTNode* CreateTree()
{
	BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));
	assert(n1);

	BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));
	assert(n2);

	BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));
	assert(n3); 
	
	BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));
	assert(n4);

	BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));
	assert(n5);

	BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));
	assert(n6);

	n1->data = 1;
	n2->data = 2;
	n3->data = 3;
	n4->data = 4;
	n5->data = 5;
	n6->data = 6;

	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n2->right = NULL;
	n4->left = n5;
	n4->right = n6;
	n3->left = NULL;
	n3->right = NULL;
	n5->left = NULL;
	n5->right = NULL;
	n6->left = NULL;
	n6->right = NULL;

	return n1;

}
int main()
{
	BTNode* root = CreateTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	printf("Tree Size is %d\n", TreeSize(root));

	printf("Tree Leaf Size is %d\n", TreeLeafSize(root));

	printf("Tree Height is %d\n", TreeHeight(root));

	printf("Tree K Level is %d\n", TreeKLevel(root, 3));

	printf("Tree Find %p\n", TreeFind(root, 4));

	BinaryTreeDestroy(root);
	return 0;
}