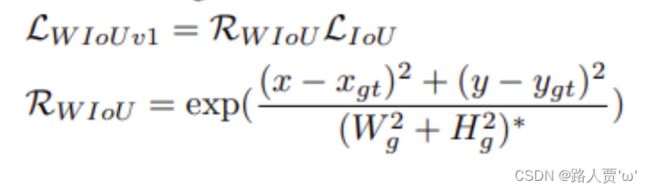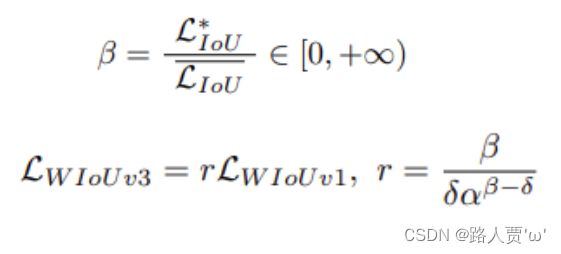损失函数:IoU、GIoU、DIoU、CIoU、EIoU、alpha IoU、SIoU、WIoU超详细精讲及Pytorch实现
前言
损失函数是用来评价模型的预测值和真实值不一样的程度,损失函数越小,通常模型的性能越好。不同的模型用的损失函数一般也不一样。
损失函数的使用主要是在模型的训练阶段,如果我们想让预测值无限接近于真实值,就需要将损失值降到最低,在这个过程中就需要引入损失函数。而损失函数的选择又是十分关键的。
一些常见的损失函数大家可以看我的这篇文章:Pytorch学习笔记(6):模型的权值初始化与损失函数
这篇我们主要讲IOU系列损失函数。
友情提示:本文干货满满,适合刚入门的小白,可以先点![]() 再慢慢看哦~
再慢慢看哦~
目录
前言
一、IOU(Intersection over Union)
1.1 简介
1.2 公式
1.3 不足
1.4 pytorch代码
二、GIOU(Generalized-IoU)
2.1 简介
2.2 公式
2.3 不足
2.4 pytorch代码
三、DIoU(Distance-IoU)
3.1 简介
3.2 公式
3.3 不足
3.4 pytorch代码
四、CIoU(Complete-IoU)
4.1 简介
4.2 公式
4.3 不足
4.4 pytorch代码
五、EIoU(Efficient-IoU)
5.1 简介
5.2 公式
5.3 pytorch代码
六、α IoU(Alpha-IoU)
6.1 简介
6.2 公式
6.3 pytorch代码
七、SIoU(SCYLLA-IoU)
7.1 简介
7.2 公式
7.3 不足
7.4 pytorch代码
八、WIoU(Wise-IoU)
8.1 简介
8.2 公式
8.3 pytorch代码
总结
一、IOU(Intersection over Union)
论文原文: 《UnitBox: An Advanced Object Detection Network》
1.1 简介
IoU全称Intersection over Union,交并比。
IoU是一种测量在特定数据集中检测相应物体准确度的一个标准。只要是在输出中得出一个预测范围(bounding boxes)的任务都可以用IoU来进行测量。
IoU算法是使用最广泛的算法,大部分的检测算法都是使用的这个算法。在目标识别中,我们的预测框与实际框的某种比值就是IoU。
![]()
1.2 公式
![]()
1.3 不足
- 如果两个框没有相交,根据定义,IoU=0,不能反映两者的距离大小(重合度)。同时因为loss=0,没有梯度回传,无法进行学习训练。(如图(a)所示)
- 当预测框和真实框的交并比相同,但是预测框所在位置不同,因为计算出来的损失一样,所以这样并不能判断哪种预测框更加准确。(如图(b)(c)所示)
1.4 pytorch代码
def IoU(box1, box2):
b1_x1, b1_y1, b1_x2, b1_y2 = box1
b2_x1, b2_y1, b2_x2, b2_y2 = box2
xx1 = np.maximum(b1_x1, b2_x1)
yy1 = np.maximum(b1_y1, b2_y1)
xx2 = np.minimum(b1_x2, b2_x2)
yy2 = np.minimum(b1_y2, b2_y2)
w = np.maximum(0.0, yy2 - yy1)
h = np.maximum(0.0, xx2 - xx1)
inter = w * h
IoU = inter/((b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter)
print("IoU: ", IoU)
if __name__ == "__main__":
box1 = np.array([100, 100, 210, 210])
box2 = np.array([150, 150, 230, 220])
IoU(box1, box2)
二、GIOU(Generalized-IoU)
论文原文: 《UnitBox: An Advanced Object Detection Network》《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》 《UnitBox: An Advanced Object Detection Network》
2.1 简介
GIoU比IoU多了一个‘Generalized’,能在更广义的层面上计算IoU。当检测框和真实框没有出现重叠的时候IoU的loss都是一样的,因此GIoU就引入了最小封闭形状C(C可以把A,B包含在内),在不重叠情况下能让预测框尽可能朝着真实框前进,这样就可以解决检测框和真实框没有重叠的问题 。
![]()
IoU取值[0,1],但是GIoU有对称区间,取值范围[-1,1]。在两者重合的时候取最大值1,在两者无交集且无限远的时候取最小值-1,因此GIoU是一个非常好的距离度量指标。
GIoU不仅可以关注重叠区域,还可以关注其他非重合区域,能比较好的反映两个框在闭包区域中的相交情况。
2.2 公式
如上图所示,绿框是Prediction框就记为A框,橙框是Ground truth框就记为B框,最外面的蓝框是将这两个矩形用最小矩形框起来的边界就记为C框,然后计算![]() ,计算这个值与C面积的比值,最后用AB的IoU减去这个比值得到GIoU。
,计算这个值与C面积的比值,最后用AB的IoU减去这个比值得到GIoU。
公式如下:
2.3 不足
- 对每个预测框与真实框均要去计算最小外接矩形,计算及收敛速度受到限制
- 在两个预测框完全重叠的情况下,不能反映出实际情况,这时GIoU就退化为IoU。
2.4 pytorch代码
def GIoU(box1, box2):
b1_x1, b1_y1, b1_x2, b1_y2 = box1
b2_x1, b2_y1, b2_x2, b2_y2 = box2
# IOU
xx1 = np.maximum(b1_x1, b2_x1)
yy1 = np.maximum(b1_y1, b2_y1)
xx2 = np.minimum(b1_x2, b2_x2)
yy2 = np.minimum(b1_y2, b2_y2)
inter_w = np.maximum(0.0, yy2 - yy1)
inter_h = np.maximum(0.0, xx2 - xx1)
inter = inter_w * inter_h
Union = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter
# GIOU
C_xx1 = np.minimum(b1_x1, b2_x1)
C_yy1 = np.minimum(b1_y1, b2_y1)
C_xx2 = np.maximum(b1_x2, b2_x2)
C_yy2 = np.maximum(b1_y2, b2_y2)
C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)
IOU = inter / Union
GIOU = IOU - abs((C_area-Union)/C_area)
print("GIOU:", GIOU)
if __name__ == "__main__":
box1 = np.array([100, 100, 210, 210])
box2 = np.array([150, 150, 230, 220])
GIoU(box1, box2)
三、DIoU(Distance-IoU)
论文原文:《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》
3.1 简介
DIoU考虑到GIoU的缺点,也是增加了C检测框,将真实框和预测框都包含了进来,但是DIoU计算的不是框之间的交并,而是计算的每个检测框之间的欧氏距离。
DIoU要比GIou更加符合目标框回归的机制,将目标与anchor之间的距离,重叠率以及尺度都考虑进去,使得目标框回归变得更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。
![]()
3.2 公式
其中d=ρ(A,B)是A框与B框中心点坐标的欧式距离,而c则是包住它们的最小方框的对角线距离。
3.3 不足
DIoU考虑了重叠面积和中心点距离,当目标框包裹预测框的时候,直接度量2个框的距离,因此DIoU收敛的更快,但并没有考虑到长宽比。
3.4 pytorch代码
def DIoU(box1, box2):
b1_x1, b1_y1, b1_x2, b1_y2 = box1
b2_x1, b2_y1, b2_x2, b2_y2 = box2
# IOU
xx1 = np.maximum(b1_x1, b2_x1)
yy1 = np.maximum(b1_y1, b2_y1)
xx2 = np.minimum(b1_x2, b2_x2)
yy2 = np.minimum(b1_y2, b2_y2)
inter_w = np.maximum(0.0, xx2 - xx1)
inter_h = np.maximum(0.0, yy2 - yy1)
inter = inter_w * inter_h
Union = (b1_x2 - b1_x1)*(b1_y2 - b1_y1) + (b2_x2 - b2_x1)*(b2_y2 - b2_y1) - inter
# DISTANCE
C_xx1 = np.minimum(b1_x1, b2_x1)
C_yy1 = np.minimum(b1_y1, b2_y1)
C_xx2 = np.maximum(b1_x2, b2_x2)
C_yy2 = np.maximum(b1_y2, b2_y2)
C_area = (C_xx2 - C_xx1) * (C_yy2 - C_yy1)
center_b_x = (b1_x1+b1_x2)/2
center_b_y = (b1_y1+b1_y2)/2
center_gtb_x = (b2_x1+b2_x2)/2
center_gtb_y = (b2_y1+b2_y2)/2
center_distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2
c_distance = (C_xx2 - C_xx1)**2 + (C_yy2 - C_yy1)**2
IOU = inter/Union
DIOU = IOU - center_distance /c_distance
print("DIOU:", DIOU)
if __name__ == "__main__":
box1 = np.array([100, 100, 210, 210])
box2 = np.array([150, 150, 230, 220])
DIoU(box1, box2)
四、CIoU(Complete-IoU)
论文原文(和DIoU同一篇论文):《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》
4.1 简介
CIoU就是在DIoU的基础上增加了检测框尺度的loss,增加了长和宽的loss,使得目标框回归更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。
4.2 公式
公式中,A,B代表两个框, ![]() 代表A和B的中心点。
代表A和B的中心点。
所以CIOU的前两部分和DIOU是一致的(这里的LOSS就是1-CIOU)。唯一增加的部分是后面的av,这个就是对长宽比的考量。
4.3 不足
- 如果预测框和gt框的长宽比是相同的,那么长宽比的惩罚项恒为0,不合理
- 观察CIoU中w, h相对于v的梯度,发现这两个梯度是一对相反数,也就是说,w和h不能同时增大或减小,这显然也不够合理的。
4.4 pytorch代码
def CIoU(box1, box2):
b1_x1, b1_y1, b1_x2, b1_y2 = box1
b2_x1, b2_y1, b2_x2, b2_y2 = box2
# IOU
xx1 = np.maximum(b1_x1, b2_x1)
yy1 = np.maximum(b1_y1, b2_y1)
xx2 = np.minimum(b1_x2, b2_x2)
yy2 = np.minimum(b1_y2, b2_y2)
inter_w = np.maximum(0.0, xx2 - xx1)
inter_h = np.maximum(0.0, yy2 - yy1)
inter = inter_w*inter_h
Union = (b1_x2-b1_x1)*(b1_y2-b1_y1) + (b2_x2-b2_x1)*(b2_y2-b2_y1) - inter
IOU = inter/Union
C_xx1 = np.minimum(b1_x1, b2_x1)
C_yy1 = np.minimum(b1_y1, b2_y1)
C_xx2 = np.maximum(b1_x2, b2_x2)
C_yy2 = np.maximum(b1_y2, b2_y2)
# DISTANCE
center_b_x = (b1_x1 + b1_x2)/2
center_b_y = (b1_y1 + b1_y2)/2
center_gtb_x = (b2_x1 + b2_x2)/2
center_gtb_y = (b2_y1 + b2_y2)/2
C_area = (C_xx2-C_xx1)*(C_yy2-C_yy1)
Distance = (center_gtb_x-center_b_x)**2 + (center_gtb_y-center_b_y)**2
Distance_area = Distance/C_area**2
# aspect ratio
pred_w = b1_y2 - b1_y1
pred_h = b1_x2 - b1_x1
gt_w = b2_y2 - b2_y1
gt_h = b2_x2 - b2_x1
v = (4/(np.pi)**2)*(np.arctan(gt_w/gt_h) - np.arctan(pred_w/pred_h))**2
alpha = v/((1-IOU) + v)
CIOU = IOU - Distance_area - alpha*v
print("CIOU:", CIOU)
if __name__ == "__main__":
box1 = np.array([100, 100, 210, 210])
box2 = np.array([150, 150, 230, 220])
CIoU(box1, box2)
五、EIoU(Efficient-IoU)
论文原文:《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》
5.1 简介
EIOU 是在 CIOU 的惩罚项基础上将预测框和真实框的纵横比的影响因子拆开,分别计算预测框和真实框的长和宽,来解决 CIOU 存在的问题。
EIoU包括三个部分:IoU损失、距离损失、高宽损失(重叠面积、中心点举例、高宽比)。高宽损失直接最小化了预测目标边界框和真实边界框的高度和宽度的差异,使其有更快的收敛速度和更好的定位结果。
![]()
5.2 公式
![]()
其中,wc和hc是预测边界框与真实边界框的最小外接矩形的宽度和高度。p是两点之间的欧氏距离。
5.3 pytorch代码
def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, EIoU=False, eps=1e-7):
# Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
box2 = box2.T
# Get the coordinates of bounding boxes
if x1y1x2y2: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
else: # transform from xywh to xyxy
b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2
# Intersection area
inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
(torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)
# Union Area
w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
union = w1 * h1 + w2 * h2 - inter + eps
iou = inter / union
if GIoU or DIoU or CIoU or EIoU:
cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1) # convex (smallest enclosing box) width
ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1) # convex height
if CIoU or DIoU or EIoU: # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
c2 = cw ** 2 + ch ** 2 + eps # convex diagonal squared
rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +
(b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4 # center distance squared
if DIoU:
return iou - rho2 / c2 # DIoU
elif CIoU: # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
with torch.no_grad():
alpha = v / (v - iou + (1 + eps))
return iou - (rho2 / c2 + v * alpha) # CIoU
elif EIoU:
rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2
rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2
cw2 = cw ** 2 + eps
ch2 = ch ** 2 + eps
return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)
else: # GIoU https://arxiv.org/pdf/1902.09630.pdf
c_area = cw * ch + eps # convex area
return iou - (c_area - union) / c_area # GIoU
else:
return iou # IoU
六、α IoU(Alpha-IoU)
论文原文:《Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression》
6.1 简介
作者将现有的基于IoU Loss推广到一个新的Power IoU系列 Loss,该系列具有一个Power IoU项和一个附加的Power正则项,具有单个Power参数α,称这种新的损失系列为α-IoU Loss。
通过调节α,使检测器在实现不同水平的bbox回归精度方面具有更大的灵活性。并且α-IoU 对小数据集和噪声的鲁棒性更强。
通过实验发现,在大多数情况下,取α=3 的效果最好。
6.2 公式
![]()
通过上图的公式我们可以看出,α-IoU 简单说就是对IoU loss家族做了幂次运算。
6.3 pytorch代码
def bbox_alpha_iou(box1, box2, x1y1x2y2=False, GIoU=False, DIoU=False, CIoU=False, alpha=3, eps=1e-7):
# Returns tsqrt_he IoU of box1 to box2. box1 is 4, box2 is nx4
box2 = box2.T
# Get the coordinates of bounding boxes
if x1y1x2y2: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
else: # transform from xywh to xyxy
b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2
# Intersection area
inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
(torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)
# Union Area
w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
union = w1 * h1 + w2 * h2 - inter + eps
# change iou into pow(iou+eps)
# iou = inter / union
iou = torch.pow(inter/union + eps, alpha)
# beta = 2 * alpha
if GIoU or DIoU or CIoU:
cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1) # convex (smallest enclosing box) width
ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1) # convex height
if CIoU or DIoU: # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
c2 = (cw ** 2 + ch ** 2) ** alpha + eps # convex diagonal
rho_x = torch.abs(b2_x1 + b2_x2 - b1_x1 - b1_x2)
rho_y = torch.abs(b2_y1 + b2_y2 - b1_y1 - b1_y2)
rho2 = ((rho_x ** 2 + rho_y ** 2) / 4) ** alpha # center distance
if DIoU:
return iou - rho2 / c2 # DIoU
elif CIoU: # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
with torch.no_grad():
alpha_ciou = v / ((1 + eps) - inter / union + v)
# return iou - (rho2 / c2 + v * alpha_ciou) # CIoU
return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha)) # CIoU
else: # GIoU https://arxiv.org/pdf/1902.09630.pdf
# c_area = cw * ch + eps # convex area
# return iou - (c_area - union) / c_area # GIoU
c_area = torch.max(cw * ch + eps, union) # convex area
return iou - torch.pow((c_area - union) / c_area + eps, alpha) # GIoU
else:
return iou # torch.log(iou+eps) or iou
七、SIoU(SCYLLA-IoU)
论文原文:《SIoU Loss: More Powerful Learning for Bounding Box Regression》
7.1 简介
SIoU考虑到期望回归之间向量的角度,重新定义角度惩罚度量,它可以使预测框快速漂移到最近的轴,随后则只需要回归一个坐标(X或Y),这有效地减少了自由度的总数。
7.2 公式
- Angle cost
(角度损失):描述了中心点(图1)连接与x-y轴之间的最小角度,当中心点在x轴或y轴上对齐时,Λ = 0。当中心点连接到x轴45°时,Λ = 1。这一惩罚可以引导anchor box移动到目标框的最近的轴上,减少了BBR的总自由度数。
![]()
![]()
-
Distance cost
(距离损失):描述了中心点之间的距离,其惩罚代价与角度代价呈正相关,当→0时,Distance cost的贡献大大降低。相反,越接近pi/4,Distance cost贡献越大。
![]()
![]()
-
Shape cost(形状损失):这里作者考虑的两框之间的长宽比,是通过计算两框之间宽之差和二者之间最大宽之比(长同理)来定义的,大体思路和CIOU类似,只不过CIOU可以的考虑是两框整体形状的收敛,而SIoU是以长、宽两个边收敛来达到整体形状收敛的效果。
![]()
-
IoU cost(IoU损失):
![]()
![]()
7.3 不足
- 模型评估结果的可重复性问题:Scylla-IoU采用了多个不同的IoU阈值,这意味着对于同一组测试数据,在不同的IoU阈值下,同一个模型的评估结果可能会有所不同。这会给模型的评估和比较带来困难。
- IoU阈值的选择问题:Scylla-IoU需要指定多个IoU阈值,而这些阈值的选择通常需要根据具体的数据集和任务进行调整。不同的IoU阈值选择可能会导致评估结果的不同,从而使得模型的比较变得困难。
- 可解释性问题:Scylla-IoU的计算过程较为复杂,需要对多个IoU阈值进行计算并进行加权平均。这可能会使得结果难以解释,给结果的可信度带来一定影响。
7.4 pytorch代码
def calculate_iou(boxes_a, boxes_b):
"""
Calculate Intersection over Union (IoU) of two bounding box tensors.
:param boxes_a: Tensor of shape (N, 4) representing bounding boxes (x1, y1, x2, y2)
:param boxes_b: Tensor of shape (M, 4) representing bounding boxes (x1, y1, x2, y2)
:return: Tensor of shape (N, M) representing IoU between all pairs of boxes_a and boxes_b
"""
# Calculate intersection coordinates
x1 = torch.max(boxes_a[:, 0].unsqueeze(1), boxes_b[:, 0].unsqueeze(0))
y1 = torch.max(boxes_a[:, 1].unsqueeze(1), boxes_b[:, 1].unsqueeze(0))
x2 = torch.min(boxes_a[:, 2].unsqueeze(1), boxes_b[:, 2].unsqueeze(0))
y2 = torch.min(boxes_a[:, 3].unsqueeze(1), boxes_b[:, 3].unsqueeze(0))
# Calculate intersection area
intersection_area = torch.clamp(x2 - x1 + 1, min=0) * torch.clamp(y2 - y1 + 1, min=0)
# Calculate box areas
boxes_a_area = (boxes_a[:, 2] - boxes_a[:, 0] + 1) * (boxes_a[:, 3] - boxes_a[:, 1] + 1)
boxes_b_area = (boxes_b[:, 2] - boxes_b[:, 0] + 1) * (boxes_b[:, 3] - boxes_b[:, 1] + 1)
# Calculate union area
union_area = boxes_a_area.unsqueeze(1) + boxes_b_area.unsqueeze(0) - intersection_area
# Calculate IoU
iou = intersection_area / union_area
return iou
def scylla_iou_loss(pred_boxes, target_boxes):
"""
Compute the SCYLLA-IoU loss between predicted and target bounding boxes.
:param pred_boxes: Tensor of shape (N, 4) representing predicted bounding boxes (x1, y1, x2, y2)
:param target_boxes: Tensor of shape (N, 4) representing target bounding boxes (x1, y1, x2, y2)
:return: SCYLLA-IoU loss
"""
iou = calculate_iou(pred_boxes, target_boxes)
# Compute SIoU terms
si = torch.min(pred_boxes[:, 2], target_boxes[:, 2]) - torch.max(pred_boxes[:, 0], target_boxes[:, 0]) + 1
sj = torch.min(pred_boxes[:, 3], target_boxes[:, 3]) - torch.max(pred_boxes[:, 1], target_boxes[:, 1]) + 1
s_union = (pred_boxes[:, 2] - pred_boxes[:, 0] + 1) * (pred_boxes[:, 3] - pred_boxes[:, 1] + 1) + \
(target_boxes[:, 2] - target_boxes[:, 0] + 1) * (target_boxes[:, 3] - target_boxes[:, 1] + 1)
s_intersection = si * sj
# Compute SCYLLA-IoU
siou = iou - (s_intersection / s_union)
# Compute loss
八、WIoU(Wise-IoU)
论文原文:《Wise-IoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism》
(论文一作是这位大佬@荷碧TongZJ,这里放上作者的论文解读: Wise-IoU 作者导读:基于动态非单调聚焦机制的边界框损失)
8.1 简介
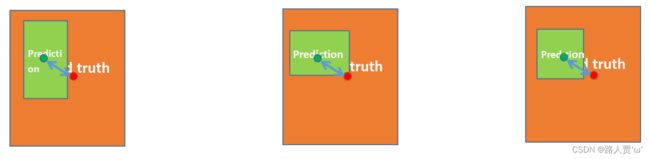
传统的Intersection over Union(IoU)只考虑了预测框和真实框的重叠部分,没有考虑两者之间的区域,导致在评估结果时可能存在偏差。基于这一思想,作者提出了一种基于IoU的损失,该损失具有动态非单调FM,名为Wise IoU(WIoU)。
8.2 公式
Wise-IoU v1:根据距离度量构建了距离注意力,得到了具有两层注意力机制的 WIoU v1:
Wise-IoU v2: 参照Focal Loss 设计了一种针对交叉熵的单调聚焦机制WIoU v2,有效降低了简单示例对损失值的贡献。这使得模型能够聚焦于困难示例,获得分类性能的提升。
Wise-IoU v3:利用 β 构造了一个非单调聚焦系数并将其应用于 WIoU v1就得到了具有动态非单调FM的WIoU v3。利用动态非单调FM的明智的梯度增益分配策略,WIoU v3获得了优越的性能。
8.3 pytorch代码
def wiou(prediction, target, weight):
"""其中,prediction和target是大小为[batch_size, height, width]的张量,
weight是大小为[batch_size, height, width]的张量,表示每个像素的权重。"""
intersection = torch.min(prediction, target) * weight
union = torch.max(prediction, target) * weight
numerator = intersection.sum(dim=(1, 2))
denominator = union.sum(dim=(1, 2)) + intersection.sum(dim=(1, 2))
iou = numerator / denominator
wiou = (1 - iou ** 2) * iou
return wiou.mean().item()
import torch
def w_iou_loss(pred_boxes, target_boxes, weight=None):
"""
Compute the Weighted IoU loss between predicted and target bounding boxes.
其中,输入pred_boxes和target_boxes分别是形状为(N, 4)的预测边界框和目标边界框张量。
如果需要使用权重,则输入形状为(N,)的权重张量weight,否则默认为None。函数返回一个标量,表示计算出的加权IoU损失。
Args:
pred_boxes (torch.Tensor): Predicted bounding boxes, with shape (N, 4).
target_boxes (torch.Tensor): Target bounding boxes, with shape (N, 4).
weight (torch.Tensor, optional): Weight tensor with shape (N,). Defaults to None.
Returns:
torch.Tensor: Weighted IoU loss scalar.
"""
# Compute the intersection over union (IoU) between the predicted and target boxes.
x1 = torch.max(pred_boxes[:, 0], target_boxes[:, 0])
y1 = torch.max(pred_boxes[:, 1], target_boxes[:, 1])
x2 = torch.min(pred_boxes[:, 2], target_boxes[:, 2])
y2 = torch.min(pred_boxes[:, 3], target_boxes[:, 3])
intersection_area = torch.clamp(x2 - x1, min=0) * torch.clamp(y2 - y1, min=0)
pred_boxes_area = (pred_boxes[:, 2] - pred_boxes[:, 0]) * (pred_boxes[:, 3] - pred_boxes[:, 1])
target_boxes_area = (target_boxes[:, 2] - target_boxes[:, 0]) * (target_boxes[:, 3] - target_boxes[:, 1])
union_area = pred_boxes_area + target_boxes_area - intersection_area
iou = intersection_area / union_area
# Compute the Weighted IoU loss using the IoU and weight tensors.
if weight is None:
w_iou = 1 - iou.mean()
else:
w_iou = (1 - iou) * weight
w_iou = w_iou.sum() / weight.sum()
return w_iou
总结
边界框回归的三大几何因素:重叠面积、中心点距离、纵横比
- IOU Loss:主要考虑检测框和目标框重叠面积。
- GIOU Loss:在IOU的基础上,解决边界框不相交时loss等于0的问题。
- DIOU Loss:在IOU和GIOU的基础上,考虑边界框中心点距离的信息。
- CIOU Loss:在DIOU的基础上,考虑边界框宽高比的尺度信息。
- EIOU Loss:在CIOU的基础上,解决了纵横比的模糊定义,并添加Focal Loss解决BBox回归中的样本不平衡问题。
- αIOU Loss:通过调节α,使探测器更灵活地实现不同水平的bbox回归精度
- SIOU Loss:在EIOU的基础上,加入了类别信息的权重因子,以提高检测模型的分类准确率。
- WIOU Loss:解决质量较好和质量较差的样本间的BBR平衡问题