二叉树的顺序存储和查找双亲结点和孩子结点与二叉树的链式存储的代码实现
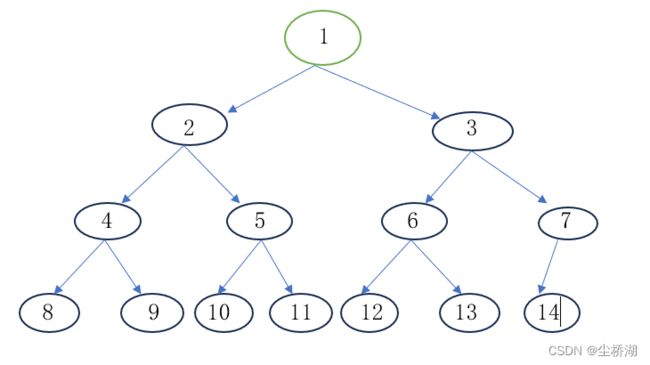
一.二叉树的顺序存储是指一组地址连续的存储单元依次自下而上,自左至右存储完全二叉树结点元素,即将完全二叉树上的编号为i的结点元素存储在一组下标为分量中。
依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适;存储结构建议从数组下标1开始存储树中的结点。
将该完全二叉树顺序存储结构用程序表示出来
1.初始化
void Init(TN L[])
{
int i;
for(i = 0; i <= Maxsize; ++i)
{
L[i].isEmpty = true;//将数组中每个结点全部定义为空
}
}2.创建数组(举有14个元素的完全二叉树的例子,因为要要找出元素是否有孩子结点,所以空间要为29)
void Creat(TN L[])
{
int i;
for(i = 1; i <= Maxsize/2; ++i)
{
L[i].value = i;//因为将其赋值的元素就是该序号
L[i].isEmpty = false;//赋值之后将其改为非空
}
}3.遍历输出
void TNPrint(TN L[])
{
int i;
for(i = 1; i <= Maxsize/2; ++i)
{
printf("%d ",L[i].value);
}
printf("\n");
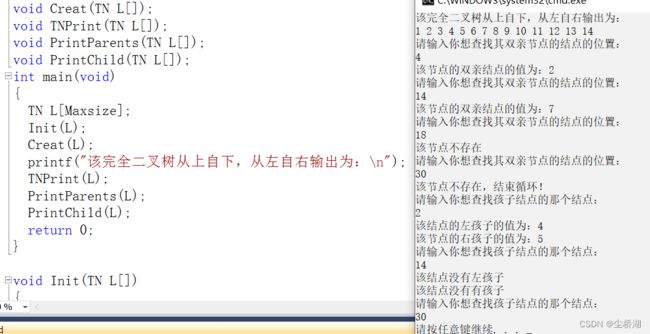
}4.查找结点的双亲结点并将其输出出来
void PrintParents(TN L[])
{
int pos = 0;//最开始定义成0
while(pos <= Maxsize)
{
printf("请输入你想查找其双亲节点的结点的位置:\n");
scanf("%d",&pos);
if(L[pos].isEmpty == true)
printf("该节点不存在\n");
else if(pos == 1)
printf("该结点为根结点,不存在双亲结点\n");
else if(pos > Maxsize)
printf("该节点不存在,结束循环!\n");
else
{
printf("该节点的双亲结点的值为:%d\n",L[pos/2].value);
}
}
}5。查找结点的孩子结点并将孩子结点的元素输出出来
void PrintChild(TN L[])
{
int pos = 0;
while(pos <= Maxsize)
{
printf("请输入你想查找孩子结点的那个结点:\n");
scanf("%d",&pos);
if(pos > Maxsize)
exit(-1);
if(L[2*pos].isEmpty == true)
printf("该结点没有左孩子\n");
else
printf("该结点的左孩子的值为:%d\n",L[2*pos].value);
if(L[2*pos+1].isEmpty == true)
printf("该结点没有有孩子\n");
else
printf("该节点的右孩子的值为:%d\n",L[2*pos+1].value);
}
}6.输出结果
二,二叉树链式存储;由于顺序存储的空间利用率较低,因此二叉树一般都是采用链式存储结构,用链表来存储二叉树中的每一个结点。
用链式存储将下列二叉树存储
1.创建二叉树
BiTree CreadBTree(void)
{
BiTNode * pA = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pB = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pC = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pD = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pE = (BiTNode *)malloc(sizeof(BiTNode));
pA->data = 'A';
pB->data = 'B';
pC->data = 'C';
pD->data = 'D';
pE->data = 'E';
pA->pLchild = pB;
pA->pRchild = pC;
pB->pLchild = pB->pRchild = NULL;
pC->pLchild = pD;
pC->pRchild = NULL;
pD->pLchild = NULL;
pD->pRchild = pE;
pE->pLchild = pE->pRchild = NULL;
return pA;
}
2.遍历输出
//先序遍历
void PreTraverseBTree(BiTree pT)
{
if(pT != NULL)
{
printf("%c\n",pT->data);
if(NULL != pT)
{
PreTraverseBTree(pT->pLchild);
}
if(NULL != pT)
{
PreTraverseBTree(pT->pRchild);
//pT->pLchild可以代表整个左子树
}
}
/*
伪算法
先访问根节点
再先序访问左子树
再先序访问右子树
*/
}
//中序遍历
void InTraverseBTree(BiTree pT)
{
if(pT != NULL)
{
if(NULL != pT)
{
InTraverseBTree(pT->pLchild);
}
printf("%c\n",pT->data);
if(NULL != pT)
{
InTraverseBTree(pT->pRchild);
//pT->pLchild可以代表整个左子树
}
}
}
//后序遍历
void PostTraverseBTree(BiTree pT)
{
if(pT != NULL)
{
if(NULL != pT)
{
PostTraverseBTree(pT->pLchild);
}
if(NULL != pT)
{
PostTraverseBTree(pT->pRchild);
//pT->pLchild可以代表整个左子树
}
printf("%c\n",pT->data);
}
}3.运行结果
顺序存储完整代码
#include
#include
//举有14个元素的完全二叉树的例子,因为要要找出元素是否有孩子结点,所以空间要为29
#define Maxsize 29
typedef struct TreeNode
{
int value;//数据域
bool isEmpty;//结点是否为空
}TN;
//函数说明
void Init(TN L[]);
void Creat(TN L[]);
void TNPrint(TN L[]);
void PrintParents(TN L[]);
void PrintChild(TN L[]);
int main(void)
{
TN L[Maxsize];
Init(L);
Creat(L);
printf("该完全二叉树从上自下,从左自右输出为:\n");
TNPrint(L);
PrintParents(L);
PrintChild(L);
return 0;
}
void Init(TN L[])
{
int i;
for(i = 0; i <= Maxsize; ++i)
{
L[i].isEmpty = true;
}
}
void Creat(TN L[])
{
int i;
for(i = 1; i <= Maxsize/2; ++i)
{
L[i].value = i;
L[i].isEmpty = false;
}
}
void TNPrint(TN L[])
{
int i;
for(i = 1; i <= Maxsize/2; ++i)
{
printf("%d ",L[i].value);
}
printf("\n");
}
void PrintParents(TN L[])
{
int pos = 0;
while(pos <= Maxsize)
{
printf("请输入你想查找其双亲节点的结点的位置:\n");
scanf("%d",&pos);
if(L[pos].isEmpty == true)
printf("该节点不存在\n");
else if(pos == 1)
printf("该结点为根结点,不存在双亲结点\n");
else if(pos > Maxsize)
printf("该节点不存在,结束循环!\n");
else
{
printf("该节点的双亲结点的值为:%d\n",L[pos/2].value);
}
}
}
void PrintChild(TN L[])
{
int pos = 0;
while(pos <= Maxsize)
{
printf("请输入你想查找孩子结点的那个结点:\n");
scanf("%d",&pos);
if(pos > Maxsize)
exit(-1);
if(L[2*pos].isEmpty == true)
printf("该结点没有左孩子\n");
else
printf("该结点的左孩子的值为:%d\n",L[2*pos].value);
if(L[2*pos+1].isEmpty == true)
printf("该结点没有有孩子\n");
else
printf("该节点的右孩子的值为:%d\n",L[2*pos+1].value);
}
} 链式存储完整代码
#include
#include
typedef struct BTNode
{
char data;
struct BTNode * pLchild;
struct BTNode * pRchild;
}BiTNode,*BiTree;
BiTree CreadBTree(void);
void PreTraverseBTree(BiTree pT);
void InTraverseBTree(BiTree pT);
void PostTraverseBTree(BiTree pT);
int main(void)
{
BiTree pT = CreadBTree();
printf("先序为:\n");
PreTraverseBTree(pT);//先序
printf("中序为:\n");
InTraverseBTree(pT);//中序
printf("后序为:\n");
PostTraverseBTree(pT);//后序
return 0;
}
void PreTraverseBTree(BiTree pT)
{
if(pT != NULL)
{
printf("%c\n",pT->data);
if(NULL != pT)
{
PreTraverseBTree(pT->pLchild);
}
if(NULL != pT)
{
PreTraverseBTree(pT->pRchild);
//pT->pLchild可以代表整个左子树
}
}
/*
伪算法
先访问根节点
再先序访问左子树
再先序访问右子树
*/
}
void InTraverseBTree(BiTree pT)
{
if(pT != NULL)
{
if(NULL != pT)
{
InTraverseBTree(pT->pLchild);
}
printf("%c\n",pT->data);
if(NULL != pT)
{
InTraverseBTree(pT->pRchild);
//pT->pLchild可以代表整个左子树
}
}
}
void PostTraverseBTree(BiTree pT)
{
if(pT != NULL)
{
if(NULL != pT)
{
PostTraverseBTree(pT->pLchild);
}
if(NULL != pT)
{
PostTraverseBTree(pT->pRchild);
//pT->pLchild可以代表整个左子树
}
printf("%c\n",pT->data);
}
}
BiTree CreadBTree(void)
{
BiTNode * pA = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pB = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pC = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pD = (BiTNode *)malloc(sizeof(BiTNode));
BiTNode * pE = (BiTNode *)malloc(sizeof(BiTNode));
pA->data = 'A';
pB->data = 'B';
pC->data = 'C';
pD->data = 'D';
pE->data = 'E';
pA->pLchild = pB;
pA->pRchild = pC;
pB->pLchild = pB->pRchild = NULL;
pC->pLchild = pD;
pC->pRchild = NULL;
pD->pLchild = NULL;
pD->pRchild = pE;
pE->pLchild = pE->pRchild = NULL;
return pA;
}