数值分析第四章节 用Python实现数值积分与数值微分
参考书籍:数值分析 第五版 李庆杨 王能超 易大义编 第4章 数值积分与数值微分
文章声明:如有发现错误,欢迎批评指正
文章目录
- 梯形公式
- 矩形公式
- 辛普森公式
- 柯特斯公式
- 复合梯形公式
- 复合辛普森公式
4.1数值积分概论
4.1.1数值积分基本思想
使用某种方法近似替代 ∫ a b f ( x ) d x = ( b − a ) f ( ξ ) \int^b_af(x)dx=(b-a)f(\xi) ∫abf(x)dx=(b−a)f(ξ)中的 f ( ξ ) f(\xi) f(ξ)避免牛顿莱布尼茨公式求积困难。更一般地我们选取区间 [ a , b ] [a,b] [a,b]的 k k k个节点,然后用 f ( x k ) f(x_k) f(xk)加权平均得到 f ( ξ ) f(\xi) f(ξ)近似值如: ∫ a b f ( x ) d x ≈ ∑ k = 0 n A k f ( x k ) \int_a^bf(x)dx\approx\sum\limits_{k=0}^nA_kf(x_k) ∫abf(x)dx≈k=0∑nAkf(xk)。
4.1.2代数精度的概念
定义1:m次代数精度(m次代数精确度)定义。一般欲使 ∫ a b f ( x ) ≈ ∑ k = 0 n A k f ( x k ) \int^b_af(x)\approx\sum\limits_{k=0}^nA_kf(x_k) ∫abf(x)≈k=0∑nAkf(xk)有m次代数精度。要求有 ∑ k = 0 n A k = b − a , ∑ k = 0 n A k x k = 1 2 ( b 2 − a 2 ) , … , ∑ k = 0 n A k x k m = 1 m + 1 ( b m + 1 − a m + 1 ) \sum\limits_{k=0}^nA_k=b-a,\sum\limits_{k=0}^nA_kx_k=\frac{1}{2}(b^2-a^2),\dots,\sum\limits_{k=0}^n A_kx_k^m=\frac{1}{m+1}(b^{m+1}-a^{m+1}) k=0∑nAk=b−a,k=0∑nAkxk=21(b2−a2),…,k=0∑nAkxkm=m+11(bm+1−am+1)。
梯形公式
因为只有两个节点 x 0 , x 1 x_0,x_1 x0,x1,所以只有两个系数 A 0 , A 1 A_0,A_1 A0,A1。如果满足代数精度为1则有 A 0 + A 1 = b − a , A 0 x 0 + A 1 x 1 = 1 2 ( b 2 − a 2 ) A_0+A_1=b-a,A_0x_0+A_1x_1=\frac{1}{2}(b^2-a^2) A0+A1=b−a,A0x0+A1x1=21(b2−a2)。两个方程但四个未知数难以求解所以对 x 0 , x 1 x_0,x_1 x0,x1作假设。 x 0 = a , x 1 = b x_0=a,x_1=b x0=a,x1=b代入方程组中解得 A 0 = A 1 = 1 2 ( b − a ) A_0=A_1=\frac{1}{2}(b-a) A0=A1=21(b−a)。带入原式有 ∫ a b f ( x ) d x ≈ b − a 2 [ f ( a ) + f ( b ) ] \int_a^bf(x)dx\approx\frac{b-a}{2}[f(a)+f(b)] ∫abf(x)dx≈2b−a[f(a)+f(b)]。
例子 : ∫ a b λ x e − λ x − 1 d x ,取 a = 0 , b = 1 , λ = 1 吧,即 ∫ 1 2 x e − x − 1 d x 例子:\int_a^{b}\lambda xe^{-\lambda x^{-1}}dx,取a=0,b=1,\lambda=1吧,即\int_1^2xe^{- x^{-1}}dx 例子:∫abλxe−λx−1dx,取a=0,b=1,λ=1吧,即∫12xe−x−1dx
反正我是积不出来我太菜了。题目来自概率论与数理统计:知 x ∼ E x p ( λ ) x\sim Exp(\lambda) x∼Exp(λ)求 E ( 1 x ) E(\frac{1}{x}) E(x1)。我感觉 E ( 1 x ) E(\frac{1}{x}) E(x1)并不存在可能是我理解错了题目意思。但是这里并不重要,只需使用数值方法求解这个定积分吧。
import math
def function(x):
return x*pow(math.e,-pow(x,-1))
print("{:.8f}".format((2-1)/2*(function(1)+function(2))))
#0.79047038
矩形公式
因为只有一个节点 x 0 x_0 x0,所以只有一个系数 A 0 A_0 A0。如果满足代数精度为1则有 A 0 = b − a , A 0 x 0 = 1 2 ( b 2 − a 2 ) A_0=b-a,A_0x_0=\frac{1}{2}(b^2-a^2) A0=b−a,A0x0=21(b2−a2)。两个方程且两个未知数直接求解。有 A 0 = b − a , x 0 = 1 2 ( a + b ) A_0=b-a,x_0=\frac{1}{2}(a+b) A0=b−a,x0=21(a+b)。代入原式有 ∫ a b f ( x ) d x ≈ ( b − a ) f ( a + b 2 ) \int_a^bf(x)dx\approx(b-a)f(\frac{a+b}{2}) ∫abf(x)dx≈(b−a)f(2a+b)。
就同样使用上面那个例子吧。
import math
def function(x):
return x*pow(math.e,-pow(x,-1))
print("{:.8f}".format((2-1)*function((2-1)/2)))
#0.06766764
4.1.3插值型的求积公式
在区间 [ a , b ] [a,b] [a,b]选取 n + 1 n+1 n+1个节点用拉格朗日插值多项式近似替代 f ( x ) f(x) f(x),即 ∫ a b f ( x ) d x \int_a^bf(x)dx ∫abf(x)dx变为 ∫ a b L n ( x ) \int_a^bL_n(x) ∫abLn(x)。公式仍然为 ∫ a b f ( x ) d x ≈ ∑ k = 0 n A k f ( x k ) \int_a^bf(x)dx\approx\sum\limits_{k=0}^nA_kf(x_k) ∫abf(x)dx≈k=0∑nAkf(xk)但是 A k A_k Ak不再由解方程组给出,为 A k = ∫ a b l k ( x ) d x , k = 0 , 1 , … , n A_k=\int_a^bl_k(x)dx,k=0,1,\dots,n Ak=∫ablk(x)dx,k=0,1,…,n。余项为 R [ f ] = ∫ a b [ f ( x ) − L n ( x ) ] d x = ∫ a b R n ( x ) d x R[f]=\int_a^b[f(x)-L_n(x)]dx=\int_a^bR_n(x)dx R[f]=∫ab[f(x)−Ln(x)]dx=∫abRn(x)dx。 R n ( x ) = f n + 1 ( ξ ) ( n + 1 ) ! ω n + 1 ( x ) , ω n + 1 ( x ) = ( x − x 0 ) ( x − x 1 ) … ( x − x n ) R_n(x)=\frac{f^{n+1}(\xi)}{(n+1)!}\omega_{n+1}(x),\omega_{n+1}(x)=(x-x_0)(x-x_1)\dots(x-x_n) Rn(x)=(n+1)!fn+1(ξ)ωn+1(x),ωn+1(x)=(x−x0)(x−x1)…(x−xn)。
4.1.4求积公式的余项
R [ f ] = ∫ a b f ( x ) d x − ∑ k = 0 n A k f ( x k ) = K f ( m + 1 ) ( η ) R[f]=\int_a^bf(x)dx-\sum\limits_{k=0}^nA_kf(x_k)=Kf^{(m+1)}(\eta) R[f]=∫abf(x)dx−k=0∑nAkf(xk)=Kf(m+1)(η)。 K K K是不依赖于 f ( x ) f(x) f(x)的待定参数。显然当 f ( x ) f(x) f(x)次数 ≤ m \leq m ≤m时, f m + 1 ( η ) = 0 f^{m+1}(\eta)=0 fm+1(η)=0所以 R [ f ] = 0 R[f]=0 R[f]=0满足m次代数精度。
4.1.5求积公式的收敛性与稳定性
定义2:在求积公式 ∫ a b f ( x ) d x ≈ ∑ k = 0 n A k f ( x k ) \int_a^bf(x)dx\approx\sum\limits_{k=0}^nA_kf(x_k) ∫abf(x)dx≈k=0∑nAkf(xk)中,若 lim n → ∞ h → 0 ∑ k = 0 n A k f k ( x k ) \lim\limits_{\begin{matrix}n\rightarrow\infty\\h\rightarrow0\end{matrix}}\sum\limits_{k=0}^nA_kf_k(x_k) n→∞h→0limk=0∑nAkfk(xk)。其中 h = max 1 ≤ i ≤ n { x i − x i − 1 } h=\max\limits_{1\leq i\leq n}\{x_i-x_{i-1}\} h=1≤i≤nmax{xi−xi−1},则称求积公式 ∫ a b f ( x ) d x ≈ ∑ k = 0 n A k f ( x k ) \int_a^bf(x)dx\approx\sum\limits_{k=0}^nA_kf(x_k) ∫abf(x)dx≈k=0∑nAkf(xk)是收敛的。
定理2:若求积公式 ∫ a b f ( x ) d x ≈ ∑ k = 0 n A k f ( x k ) \int_a^bf(x)dx\approx\sum\limits_{k=0}^nA_kf(x_k) ∫abf(x)dx≈k=0∑nAkf(xk)中系数 A k > 0 ( k = 0 , 1 , … , n ) A_k>0(k=0,1,\dots,n) Ak>0(k=0,1,…,n),则此求积公式是稳定的。
4.2牛顿-柯特斯公式
4.2.1柯特斯系数与辛普森公式
设将积分区间 [ a , b ] [a,b] [a,b]划分为n等份,步长 h = b − a n h=\frac{b-a}{n} h=nb−a,选取等距节点 x k = a + k h x_k=a+kh xk=a+kh构造出的插值型求积公式 I n = ( b − a ) ∑ k = 0 n C k ( n ) f ( x k ) I_n=(b-a)\sum\limits_{k=0}^nC_k^{(n)}f(x_k) In=(b−a)k=0∑nCk(n)f(xk),称为牛顿-柯特斯公式,式中 C k ( n ) C_k^{(n)} Ck(n)称为柯特斯系数。由于这是插值型的求积公式所以有 A k = ( b − a ) C k ( n ) A_k=(b-a)C_k^{(n)} Ak=(b−a)Ck(n)并且有 A k = ∫ a b l k ( x ) d x , k = 0 , 1 , … , n A_k=\int_a^bl_k(x)dx,k=0,1,\dots,n Ak=∫ablk(x)dx,k=0,1,…,n(这个之前已经说过)。柯特斯系数的理论求解是可行的因为全部是多项式;但是还是记住考试谁想算啊,记住 ≤ 4 \leq 4 ≤4的应该就好。当 n = 1 n=1 n=1时为梯形公式有 c 0 ( 1 ) = c 1 ( 1 ) = 1 2 c_0^{(1)}=c_1^{(1)}=\frac{1}{2} c0(1)=c1(1)=21。
辛普森公式
当 n = 2 n=2 n=2时为辛普森公式有 c 0 ( 2 ) = c 2 ( 2 ) = 1 6 , c 1 ( 2 ) = 2 3 c_0^{(2)}=c_2^{(2)}=\frac{1}{6},c_1^{(2)}=\frac{2}{3} c0(2)=c2(2)=61,c1(2)=32。
就同样使用上面那个例子吧。
import math
def function(x):
return x*pow(math.e,-pow(x,-1))
print("{:.8f}".format((2-1)*(1/6*function(1)+2/3*function((2-1)/2)+1/6*function(2))))
#0.30860189
记一下 n = 3 n=3 n=3时的系数
柯特斯公式
当 n = 4 n=4 n=4时为柯特斯公式有 c 0 ( 4 ) = c 4 ( 4 ) = 7 90 , c 1 ( 4 ) = c 3 ( 4 = 16 45 , c 2 4 = 2 15 c_0^{(4)}=c_4^{(4)}=\frac{7}{90},c_1^{(4)}=c_3^{(4}=\frac{16}{45},c_2^{4}=\frac{2}{15} c0(4)=c4(4)=907,c1(4)=c3(4=4516,c24=152。
就同样使用上面那个例子吧。
import math
def function1(x):
return x*pow(math.e,-pow(x,-1))
def function2():
cnt=0;lt=[7/90,16/45,2/15,16/45,7/90]
for i in range(5):
cnt+=lt[i]*function1(1+i*(2-1)/4)
return cnt
print("{:.8f}".format(function2()))
#0.77672741
4.2.2偶阶求积公式的代数精度
当阶 n n n为欧式时,牛顿-柯特斯公式至少有 n + 1 n+1 n+1次代数精度。
4.2.3辛普森公式的余项
算就好了,不难算的。我们来推一下一般。前面已经说了K不依赖于 f ( x ) f(x) f(x),不妨令 f ( x ) = x m + 1 f(x)=x^{m+1} f(x)=xm+1,所以有 K = ∫ a b f ( x ) d x − ∑ k = 0 n A k f ( x k ) f ( m + 1 ) ( η ) = ∫ a b x m + 1 d x − ∑ k = 0 n A k f ( x k ) ( m + 1 ) ! = 1 m + 2 ( b m + 2 − a m + 2 ) − ∑ k = 0 n A k f ( x k ) ( m + 1 ) ! K=\frac{\int_a^bf(x)dx-\sum\limits_{k=0}^nA_kf(x_k)}{f^{(m+1)}(\eta)}=\frac{\int_a^bx^{m+1}dx-\sum\limits_{k=0}^nA_kf(x_k)}{(m+1)!}=\frac{\frac{1}{m+2}(b^{m+2}-a^{m+2})-\sum\limits_{k=0}^nA_kf(x_k)}{(m+1)!} K=f(m+1)(η)∫abf(x)dx−k=0∑nAkf(xk)=(m+1)!∫abxm+1dx−k=0∑nAkf(xk)=(m+1)!m+21(bm+2−am+2)−k=0∑nAkf(xk)。所以有 R [ f ] = K f ( m + 1 ) ( η ) R[f]=Kf^{(m+1)}(\eta) R[f]=Kf(m+1)(η)。
4.3复合求积公式
就是一种简单套路。没啥可以拿来说的。
4.3.1复合梯形公式
4.3.2复合辛普森公式
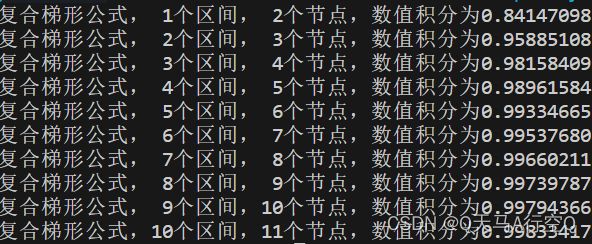
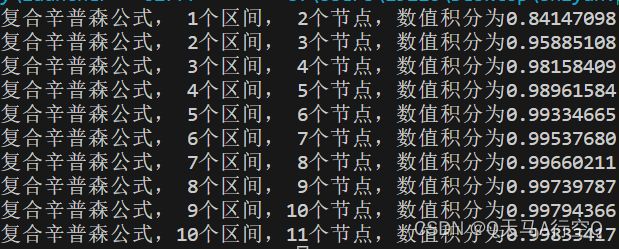
例 3 : f ( x ) = ∫ 0 1 s i n x x d x 例3:f(x)=\int_0^1\frac{sinx}{x}dx 例3:f(x)=∫01xsinxdx
复合梯形公式
from math import sin
def function2(x):
return sin(x)/x
def function1(n):
lt=[0+1/n for i in range(n+1)]
cnt=0
for i in range(n):
cnt+=1/n*((function2(lt[i])+function2(lt[i+1]))/2)
return cnt
for i in range(10):
print("复合梯形公式,{:>2d}个区间,{:>2d}个节点,数值积分为{:>10.8f}".format(i+1,i+2,function1(i+1)))
复合辛普森公式
from math import sin
def function2(x):
return sin(x)/x
def function1(n):
lt=[0+1/n for i in range(n+1)]
cnt=0
for i in range(n):
cnt+=1/n*(1/6*function2(lt[i])+2/3*function2((lt[i]+lt[i+1])/2)+1/6*function2(lt[i+1]))
return cnt
for i in range(10):
print("复合辛普森公式,{:>2d}个区间,{:>2d}个节点,数值积分为{:>10.8f}".format(i+1,i+2,function1(i+1)))