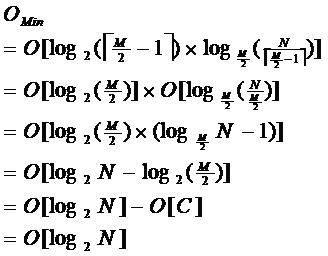B树索引

http://space.itpub.net/9842/viewspace-312607

摘要：本文对B树索引的结构、内部管理等方面做了一个全面的介绍。同时深入探讨了一些与B树索引有关的广为流传的说法，比如删除记录对索引的影响，定期重建索引能解决许多性能问题等。

<!--[if !supportLists]-->1.B树索引的相关概念

索引与表一样，也属于段（segment）的一种。里面存放了用户的数据，跟表一样需要占用磁盘空间。只

不过，在索引里的数据存放形式与表里的数据存放形式非常的不一样。在理解索引时，可以想象一本书，其中书的内容就相当于表里的数据，而书前面的目录就相当于该表的索引。同时，通常情况下，索引所占用的磁盘空间要比表要小的多，其主要作用是为了加快对数据的搜索速度，也可以用来保证数据的唯一性。

      但是，索引作为一种可选的数据结构，你可以选择为某个表里的创建索引，也可以不创建。这是因为一旦创建了索引，就意味着oracle对表进行DML（包括INSERT、UPDATE、DELETE）时，必须处理额外的工作量（也就是对索引结构的维护）以及存储方面的开销。所以创建索引时，需要考虑创建索引所带来的查询性能方面的提高，与引起的额外的开销相比，是否值得。

      从物理上说，索引通常可以分为：分区和非分区索引、常规B树索引、位图（bitmap）索引、翻转（reverse）索引等。其中，B树索引属于最常见的索引，由于我们的这篇文章主要就是对B树索引所做的探讨，因此下面只要说到索引，都是指B树索引。

      B树索引是一个典型的树结构，其包含的组件主要是：

<!--[if !supportLists]-->1)     <!--[endif]-->叶子节点（Leaf node）：包含条目直接指向表里的数据行。

<!--[if !supportLists]-->2)     <!--[endif]-->分支节点（Branch node）：包含的条目指向索引里其他的分支节点或者是叶子节点。

<!--[if !supportLists]-->3)     <!--[endif]-->根节点（Root node）：一个B树索引只有一个根节点，它实际就是位于树的最顶端的分支节点。

可以用下图一来描述B树索引的结构。其中，B表示分支节点，而L表示叶子节点。

对于分支节点块（包括根节点块）来说，其所包含的索引条目都是按照顺序排列的（缺省是升序排列，也可以在创建索引时指定为降序排列）。每个索引条目（也可以叫做每条记录）都具有两个字段。第一个字段表示当前该分支节点块下面所链接的索引块中所包含的最小键值；第二个字段为四个字节，表示所链接的索引块的地址，该地址指向下面一个索引块。在一个分支节点块中所能容纳的记录行数由数据块大小以及索引键值的长度决定。比如从上图一可以看到，对于根节点块来说，包含三条记录，分别为（0 B1）、（500 B2）、（1000 B3），它们指向三个分支节点块。其中的0、500和1000分别表示这三个分支节点块所链接的键值的最小值。而B1、B2和B3则表示所指向的三个分支节点块的地址。

      对于叶子节点块来说，其所包含的索引条目与分支节点一样，都是按照顺序排列的（缺省是升序排列，也可以在创建索引时指定为降序排列）。每个索引条目（也可以叫做每条记录）也具有两个字段。第一个字段表示索引的键值，对于单列索引来说是一个值；而对于多列索引来说则是多个值组合在一起的。第二个字段表示键值所对应的记录行的ROWID，该ROWID是记录行在表里的物理地址。如果索引是创建在非分区表上或者索引是分区表上的本地索引的话，则该ROWID占用6个字节；如果索引是创建在分区表上的全局索引的话，则该ROWID占用10个字节。

      知道这些信息以后，我们可以举个例子来说明如何估算每个索引能够包含多少条目，以及对于表来说，所产生的索引大约多大。对于每个索引块来说，缺省的PCTFREE为10％，也就是说最多只能使用其中的90％。同时9i以后，这90％中也不可能用尽，只能使用其中的87％左右。也就是说，8KB的数据块中能够实际用来存放索引数据的空间大约为6488（8192×90％×88％）个字节。

      假设我们有一个非分区表，表名为warecountd，其数据行数为130万行。该表中有一个列，列名为goodid，其类型为char（8），那么也就是说该goodid的长度为固定值：8。同时在该列上创建了一个B树索引。

在叶子节点中，每个索引条目都会在数据块中占一行空间。每一行用2到3个字节作为行头，行头用来存放标记以及锁定类型等信息。同时，在第一个表示索引的键值的字段中，每一个索引列都有1个字节表示数据长度，后面则是该列具体的值。那么对于本例来说，在叶子节点中的一行所包含的数据大致如下图二所示：

从上图可以看到，在本例的叶子节点中，一个索引条目占18个字节。同时我们知道8KB的数据块中真正可以用来存放索引条目的空间为6488字节，那么在本例中，一个数据块中大约可以放360（6488/18）个索引条目。而对于我们表中的130万条记录来说，则需要大约3611（1300000/360）个叶子节点块。

      而对于分支节点里的一个条目（一行）来说，由于它只需保存所链接的其他索引块的地址即可，而不需要保存具体的数据行在哪里，因此它所占用的空间要比叶子节点要少。分支节点的一行中所存放的所链接的最小键值所需空间与上面所描述的叶子节点相同；而存放的索引块的地址只需要4个字节，比叶子节点中所存放的ROWID少了2个字节，少的这2个字节也就是ROWID中用来描述在数据块中的行号所需的空间。因此，本例中在分支节点中的一行所包含的数据大致如下图三所示：

从上图可以看到，在本例的分支节点中，一个索引条目占16个字节。根据上面叶子节点相同的方式，我们可以知道一个分支索引块可以存放大约405（6488/16）个索引条目。而对于我们所需要的3611个叶子节点来说，则总共需要大约9个分支索引块。

      这样，我们就知道了我们的这个索引有2层，第一层为1个根节点，第二层为9个分支节点，而叶子节点数为3611个，所指向的表的行数为1300000行。但是要注意，在oracle的索引中，层级号是倒过来的，也就是说假设某个索引有N层，则根节点的层级号为N，而根节点下一层的分支节点的层级号为N-1，依此类推。对本例来说，9个分支节点所在的层级号为1，而根节点所在的层级号为2。

 

 

 

 

 

 

 

http://www.cublog.cn/u/14468/showart_441875.html

B树、B-树、B+树、B*树都是什么

 

B树

       即二叉搜索树：

       1.所有非叶子结点至多拥有两个儿子（Left和Right）；

       2.所有结点存储一个关键字；

       3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

       如：

       

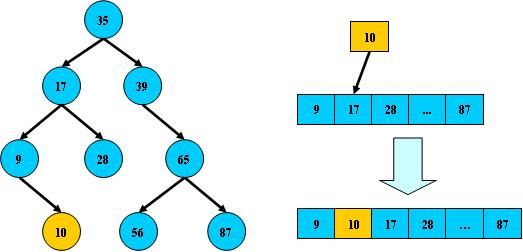
       B树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；

       如果B树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变B树结构（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销；

       如：

      

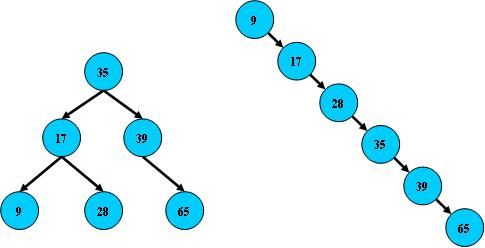
   但B树在经过多次插入与删除后，有可能导致不同的结构：

   右边也是一个B树，但它的搜索性能已经是线性的了；同样的关键字集合有可能导致不同的树结构索引；所以，使用B树还要考虑尽可能让B树保持左图的结构，和避免右图的结构，也就是所谓的“平衡”问题；      

       实际使用的B树都是在原B树的基础上加上平衡算法，即“平衡二叉树”；如何保持B树结点分布均匀的平衡算法是平衡二叉树的关键；平衡算法是一种在B树中插入和删除结点的策略；

 

B-树

       是一种多路搜索树（并不是二叉的）：

       1.定义任意非叶子结点最多只有M个儿子；且M>2；

       2.根结点的儿子数为[2, M]；

       3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

       4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

       5.非叶子结点的关键字个数=指向儿子的指针个数-1；

       6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

       7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

       8.所有叶子结点位于同一层；

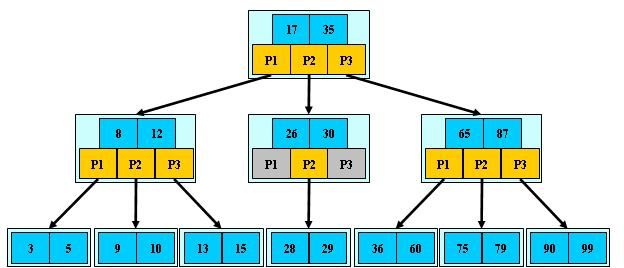
       如：（M=3）

       B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；

B-树的特性：

       1.关键字集合分布在整颗树中；

       2.任何一个关键字出现且只出现在一个结点中；

       3.搜索有可能在非叶子结点结束；

       4.其搜索性能等价于在关键字全集内做一次二分查找；

       5.自动层次控制；

       由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少利用率，其最底搜索性能为：

    

       其中，M为设定的非叶子结点最多子树个数，N为关键字总数；

       所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；

       由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；

 

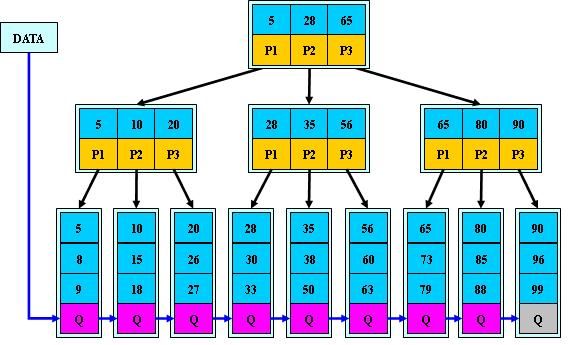
B+树

       B+树是B-树的变体，也是一种多路搜索树：

       1.其定义基本与B-树同，除了：

       2.非叶子结点的子树指针与关键字个数相同；

       3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；

       5.为所有叶子结点增加一个链指针；

       6.所有关键字都在叶子结点出现；

       如：（M=3）

   B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

       B+的特性：

       1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

       2.不可能在非叶子结点命中；

       3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

       4.更适合文件索引系统；

   

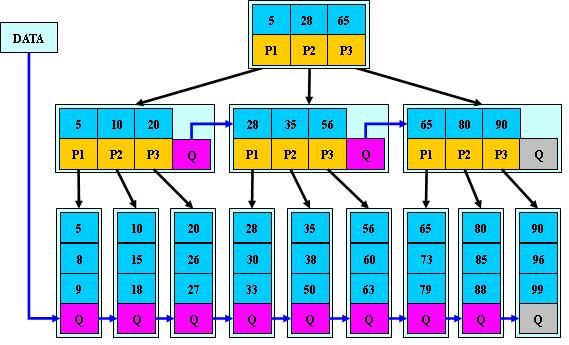
B*树

       是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；

   B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）；

       B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

       B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

       所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

   

小结

       B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

       B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；

       所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

       B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

       B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；