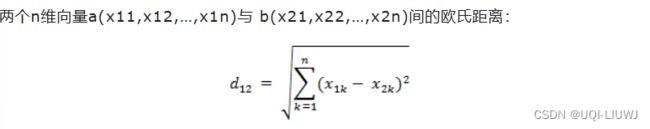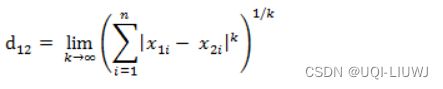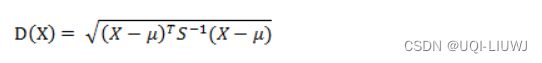算法笔记\python 笔记： 相似性度量

1 欧氏距离

 

1.1 python实现：

from scipy.spatial import distance
distance.euclidean([1,2],[2,1])
#1.4142135623730951

1.2 标准化欧氏距离

先将数据标准化

 

（减去的均值两两抵消）

 2 曼哈顿距离

又称为城市街区距离

2.1 python 实现

from scipy.spatial import distance
distance.cityblock([1,2],[2,1])
#2

 3 切比雪夫距离

也称为棋盘距离，因为它是两个实值向量之间任意维度上的最大距离

 等价形式

3.1 python实现

from scipy.spatial import distance
distance.chebyshev([1,2],[2,1])
#1

 4 闵可夫斯基距离 minkowski

当p=1时，就是曼哈顿距离

当p=2时，就是欧氏距离

当p→∞时，就是切比雪夫距离

4.1 闵可夫斯基距离的缺点

• 各个分量的量纲(scale)，也就是“单位”当作相同的看待
• 没有考虑各个分量的分布（期望，方差等)可能是不同的
  • eg，二维样本(身高,体重)，有三个样本：a(180,50)，b(190,50)，c(180,60)。
    • 那么a与b之间的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c之间的闵氏距离，但是身高的10cm真的等价于体重的10kg么？

4.2 python实现

from scipy.spatial import distance
distance.minkowski([1,2],[2,1],4)
#1.189207115002721

5 马氏距离 Mahalanobis

• 有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，
  • 其中样本向量X到μ的马氏距离
    • 
  • 其中向量Xi与Xj之间的马氏距离
    • 

• ——>马氏距离和量纲无关，排除变量之间的相关性的干扰

6 夹角余弦

6.1 python实现

from scipy.spatial import distance
distance.cosine([1,2],[2,1])
#0.19999999999999996

 7 汉明距离

两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数

例如字符串“1111”与“1001”之间的汉明距离为2。

对向量按元素进行比较，并对差异的数量进行平均

如果两个向量相同，得到的距离是0之间，如果两个向量完全不同，得到的距离是1

from scipy.spatial import distance
distance.hamming([1,2],[2,1])
# 1 
# 第一个元素和第二个元素都不同，所以汉明距离为(1+1)/2=1


distance.hamming([1,2],[1,1])
#0.5
#(1+0)/2=0.5

8 杰卡德距离 Jaccard

8.1 杰卡德相似系数

8.2 杰卡德距离

8.2.1 python 实现

from scipy.spatial import distance
distance.jaccard([1,2],[2,1])
#1


distance.jaccard([1,1],[2,1])
#0.5

9 相关距离

9.1 相关系数

•  相关系数的取值范围是[-1,1]。
  • 相关系数的绝对值越大，则表明X与Y相关度越高。
  • 当X与Y线性相关时，相关系数取值为1（正线性相关）或-1（负线性相关）

9.2 相关距离

10 半正矢距离 haversine

• 球面上两点之间的最短距离
  • 常用于导航
  • 经度、纬度和曲率对计算都有影响

10.1 python 实现

from sklearn.metrics.pairwise import haversine_distances
haversine_distances([[1,2],[2,1]])
'''
array([[0.        , 0.87152123],
       [0.87152123, 0.        ]])
'''

 参考内容：机器学习中的相似性度量总结 (qq.com)