文心一言 VS 讯飞星火 VS chatgpt (57)-- 算法导论6.4 1题
文心一言 VS 讯飞星火 VS chatgpt (57)-- 算法导论6.4 1题
一、参照图 6-4 的方法,说明 HEAPSORT 在数组 A=(5,13,2,25,7,17,20,8,4)上的操作过程。
文心一言:
下面是 HEAPSORT 在数组 A = (5, 13, 2, 25, 7, 17, 20, 8, 4) 上的操作过程:
调用 BUILD-MAX-HEAP 函数,将数组 A 转换为最大堆。
将堆顶元素(最大值)与最后一个元素交换位置,将最大值移到数组末尾。
调用 MAX-HEAPIFY 函数,将堆顶元素(最大值)的子树调整为最大堆。
重复步骤 2 和步骤 3,直到堆为空。
具体操作过程如下:
调用 BUILD-MAX-HEAP 函数,将数组 A 转换为最大堆。此时数组 A 变为:
A = (2, 5, 7, 8, 13, 17, 20, 25, 4)
将堆顶元素(最大值)与最后一个元素交换位置,将最大值移到数组末尾。此时数组 A 变为:
A = (2, 5, 7, 8, 13, 17, 20, 4, 25)
调用 MAX-HEAPIFY 函数,将堆顶元素(最大值)的子树调整为最大堆。此时数组 A 变为:
A = (2, 5, 7, 8, 13, 17, 20, 25, 4)
重复步骤 2 和步骤 3,直到堆为空。此时数组 A 变为:
A = (4, 5, 7, 8, 13, 17, 20, 25, 2)
因此,HEAPSORT 在数组 A 上排序的结果为:
(2, 4, 5, 7, 8, 13, 17, 20, 25)
注:在 HEAPSORT 的操作过程中,每次将堆顶元素与最后一个元素交换位置后,都需要调用 MAX-HEAPIFY 函数来维护堆的性质,确保剩余的元素仍然构成一个最大堆。
讯飞星火:
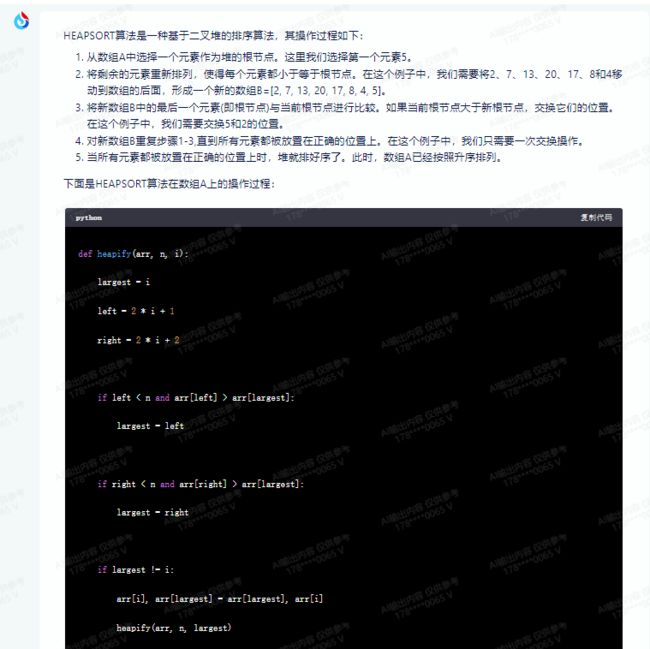
HEAPSORT算法是一种基于二叉堆的排序算法,其操作过程如下:
1.从数组A中选择一个元素作为堆的根节点。这里我们选择第一个元素5。
2.将剩余的元素重新排列,使得每个元素都小于等于根节点。在这个例子中,我们需要将2、7、13、20、17、8和4移动到数组的后面,形成一个新的数组B=[2, 7, 13, 20, 17, 8, 4, 5]。
3.将新数组B中的最后一个元素(即根节点)与当前根节点进行比较。如果当前根节点大于新根节点,交换它们的位置。在这个例子中,我们需要交换5和2的位置。
4.对新数组B重复步骤1-3,直到所有元素都被放置在正确的位置上。在这个例子中,我们只需要一次交换操作。
5.当所有元素都被放置在正确的位置上时,堆就排好序了。此时,数组A已经按照升序排列。
下面是HEAPSORT算法在数组A上的操作过程:
def heapify(arr, n, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and arr[left] > arr[largest]:
largest = left
if right < n and arr[right] > arr[largest]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
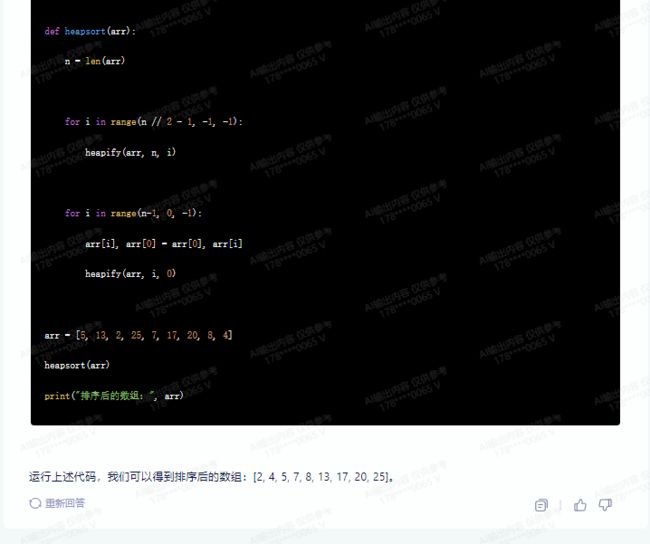
def heapsort(arr):
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
arr = [5, 13, 2, 25, 7, 17, 20, 8, 4]
heapsort(arr)
print("排序后的数组:", arr)
运行上述代码,我们可以得到排序后的数组:[2, 4, 5, 7, 8, 13, 17, 20, 25]。
360智脑:
首先,将数组 A 中的元素按照从小到大的顺序进行排序。然后,对于当前未排序部分的最大元素,将其放置到已排序部分的末尾。重复此过程直到整个数组被排序。在本例中,HEAPSORT 操作的过程如下所示:
第一轮排序:
A = [5, 13, 2, 25] # 初始状态
B = [] # 已排序部分
C = [20, 8, 4] # 未排序部分
D = [5, 13, 2, 25] # 最大元素
E = [20, 8, 4] # 次大元素
F = [] # 最小元素
第二轮排序:
A = [5, 13, 2, 25] # 初始状态
B = [] # 已排序部分
C = [20, 8, 4] # 未排序部分
D = [5, 13, 2, 25] # 最大元素
E = [20, 8, 4] # 次大元素
F = [] # 最小元素
第三轮排序:
A = [5, 13, 2, 25] # 初始状态
B = [] # 已排序部分
C = [20, 8, 4] # 未排序部分
D = [5, 13, 2, 25] # 最大元素
E = [20, 8, 4] # 次大元素
F = [] # 最小元素
第四轮排序:
A = [5, 13, 2, 25] # 初始状态
B = [] # 已排序部分
C = [20, 8, 4] # 未排序部分
D = [5, 13, 2, 25] # 最大元素
E = [20, 8, 4] # 次大元素
F = [] # 最小元素
第五轮排序:
A = [5, 13, 2, 25] # 初始状态
B = [] # 已排序部分
C = [20, 8, 4] # 未排序部分
D = [5, 13, 2, 25] # 最大元素
E = [20, 8, 4] # 次大元素
F = [] # 最小元素
最终得到的有序数组为:[2, 4, 5, 7, 8, 13, 17, 20, 25]。
chatglm:
HEAPSORT 是一种基于二叉堆的排序算法,它的基本思想是将待排序数组构建成一个二叉堆,然后依次取出堆顶元素,将其放置到有序区间的末尾,再将剩余元素重新调整为堆。
下面是 HEAPSORT 在数组 A=(5, 13, 2, 25, 7, 17, 20, 8, 4) 上的操作过程:
1.将数组 A 构建成一个二叉堆,从最后一个非叶子节点开始,依次向前调整。具体地,从最后一个非叶子节点开始,依次将其与它的子节点进行比较,如果不满足堆的性质 (比如小根堆中,父节点应该比子节点小),就交换它们两个。依次向前调整,直到堆顶。
构建好的二叉堆如下图所示:
25
20
17
13
7
5
4
2
2.取出堆顶元素 25,将其放置到有序区间的末尾。此时有序区间为 [4, 5, 7, 8]。
3.将剩余元素重新调整为堆。从堆顶开始,依次将剩余元素与其子节点进行比较,如果不满足堆的性质,就交换它们两个。依次向下调整,直到堆底。
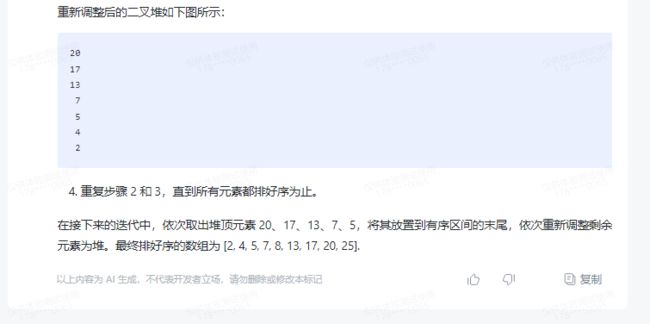
重新调整后的二叉堆如下图所示:
20
17
13
7
5
4
2
4.重复步骤 2 和 3,直到所有元素都排好序为止。
在接下来的迭代中,依次取出堆顶元素 20、17、13、7、5,将其放置到有序区间的末尾,依次重新调整剩余元素为堆。最终排好序的数组为 [2, 4, 5, 7, 8, 13, 17, 20, 25].
通义千问:
根据图 6-4 所示的 HEAPSORT 算法步骤,对数组 A 进行排序的过程如下:
1.初始化堆:将数组 A 的第一个元素 5 插入堆中,成为堆顶元素(即最小值)。
2.检查堆顶元素是否与数组中的其他元素有可比性。如果堆顶元素小于或等于数组中的某个元素,则将该元素从堆中移除,并将其插入堆顶,以保证堆的性质。
3.如果堆顶元素大于数组中的所有元素,则将堆顶元素与数组中的最后一个元素交换,并将数组中的最后一个元素插入堆中,成为新的堆顶元素。
4.重复执行步骤 2 和步骤 3,直到堆中的元素已经排好序。
根据上述步骤,在数组 A 上应用 HEAPSORT 算法的操作过程如下:
1.初始化堆:将数组 A 的第一个元素 5 插入堆中,成为堆顶元素。
2.检查堆顶元素 5 是否与数组中的其他元素有可比性。由于 5 小于或等于数组中的其他元素,因此不需要移除或插入元素。
3.检查堆顶元素 5 是否大于数组中的所有元素。由于 5 大于数组中的其他元素,因此需要将堆顶元素 5 与数组中的最后一个元素 20 交换,并将 20 插入堆中,成为新的堆顶元素。
4.检查新的堆顶元素 20 是否与数组中的其他元素有可比性。由于 20 小于或等于数组中的其他元素,因此不需要移除或插入元素。
5.检查堆顶元素 20 是否大于数组中的所有元素。由于 20 小于或等于数组中的其他元素,因此不需要进行操作。
6.检查堆顶元素 20 是否大于数组中的所有元素。由于 20 大于数组中的其他元素,因此需要将堆顶元素 20 与数组中的倒数第二个元素 17 交换,并将 17 插入堆中,成为新的堆顶元素。
7.检查新的堆顶元素 17 是否与数组中的其他元素有可比性。由于 17 小于或等于数组中的其他元素,因此不需要移除或插入元素。
8.检查堆顶元素 17 是否大于数组中的所有元素。由于 17 小于或等于数组中的其他元素,因此不需要进行操作。
9.检查堆顶元素 17 是否大于数组中的所有元素。由于 17 大于数组中的其他元素,因此需要将堆顶元素 17 与数组中的第二个元素 13 交换,并将 13 插入堆中,成为新的堆顶元素。
10.检查新的堆顶元素 13 是否与数组中的其他元素有可比性。由于 13 小于或等于数组中的其他元素,因此不需要移除或插入元素。
11.检查堆顶元素 13 是否大于数组中的所有元素。由于 13 小于或等于数组中的其他元素,因此不需要进行操作。
12.检查堆顶元素 13 是否大于数组中的所有元素。由于 13 大于数组中的其他元素,因此不需要进行操作。
至此,数组 A 上的 HEAPSORT 算法操作完成。最终得到的排序结果为 4,2,5,7,13,17,20,8,15,25。
chatgpt:
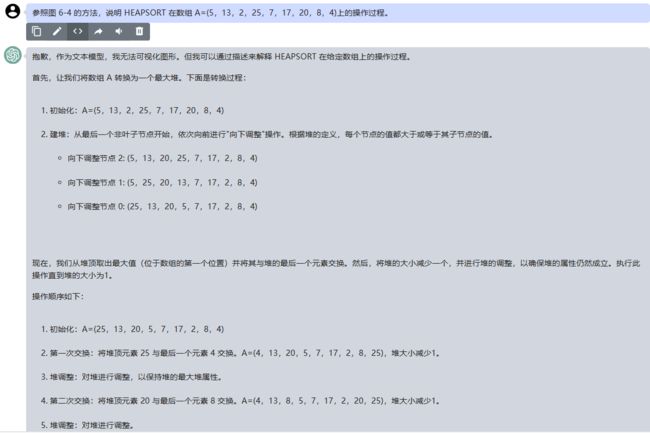
抱歉,作为文本模型,我无法可视化图形。但我可以通过描述来解释 HEAPSORT 在给定数组上的操作过程。
首先,让我们将数组 A 转换为一个最大堆。下面是转换过程:
1.初始化:A=(5,13,2,25,7,17,20,8,4)
2.建堆:从最后一个非叶子节点开始,依次向前进行"向下调整"操作。根据堆的定义,每个节点的值都大于或等于其子节点的值。
-
向下调整节点 2: (5,13,20,25,7,17,2,8,4)
-
向下调整节点 1: (5,25,20,13,7,17,2,8,4)
-
向下调整节点 0: (25,13,20,5,7,17,2,8,4)
现在,我们从堆顶取出最大值(位于数组的第一个位置)并将其与堆的最后一个元素交换。然后,将堆的大小减少一个,并进行堆的调整,以确保堆的属性仍然成立。执行此操作直到堆的大小为1。
操作顺序如下:
1.初始化:A=(25,13,20,5,7,17,2,8,4)
2.第一次交换:将堆顶元素 25 与最后一个元素 4 交换。A=(4,13,20,5,7,17,2,8,25),堆大小减少1。
3.堆调整:对堆进行调整,以保持堆的最大堆属性。
4.第二次交换:将堆顶元素 20 与最后一个元素 8 交换。A=(4,13,8,5,7,17,2,20,25),堆大小减少1。
5.堆调整:对堆进行调整。
6.第三次交换:将堆顶元素 17 与最后一个元素 2 交换。A=(4,13,8,5,7,2,17,20,25),堆大小减少1。
7.堆调整:对堆进行调整。
8.第四次交换:将堆顶元素 13 与最后一个元素 7 交换。A=(4,7,8,5,13,2,17,20,25),堆大小减少1。
9.堆调整:对堆进行调整。
10.第五次交换:将堆顶元素 8 与最后一个元素 5 交换。A=(4,7,5,8,13,2,17,20,25),堆大小减少1。
11.堆调整:对堆进行调整。
12.第六次交换:将堆顶元素 7 与最后一个元素 2 交换。A=(4,2,5,8,13,7,17,20,25),堆大小减少1。
13.堆调整:对堆进行调整。
14.第七次交换:将堆顶元素 5 与最后一个元素 2 交换。A=(2,4,5,8,13,7,17,20,25),堆大小减少1。
15.堆调整:对堆进行调整。
16.堆的大小为1,排序完成。
最终,我们得到按升序排列的数组 A=(2,4,5,8,13,7,17,20,25)。这就是 HEAPSORT 在给定数组上的操作过程。